Vibration Analysis Of Timber Floors [Eurocode]

One disadvantage of timber floors is its vibration behaviour because of its little weight.
Vibration is a phenomenon in structural engineering that needs to be investigated for light-weight structures like timber floors or steel staircases. Because if the frequencies are too little, people might feel unwell.
In many cases, that’s the vibration analysis is the most critical verification of timber floors.
In this article, I’ll show you how to verify timber joist floors for vibration.
Now, let’s get into it.
The 3 Steps To Verify Timber Floors for Vibration According To Eurocode
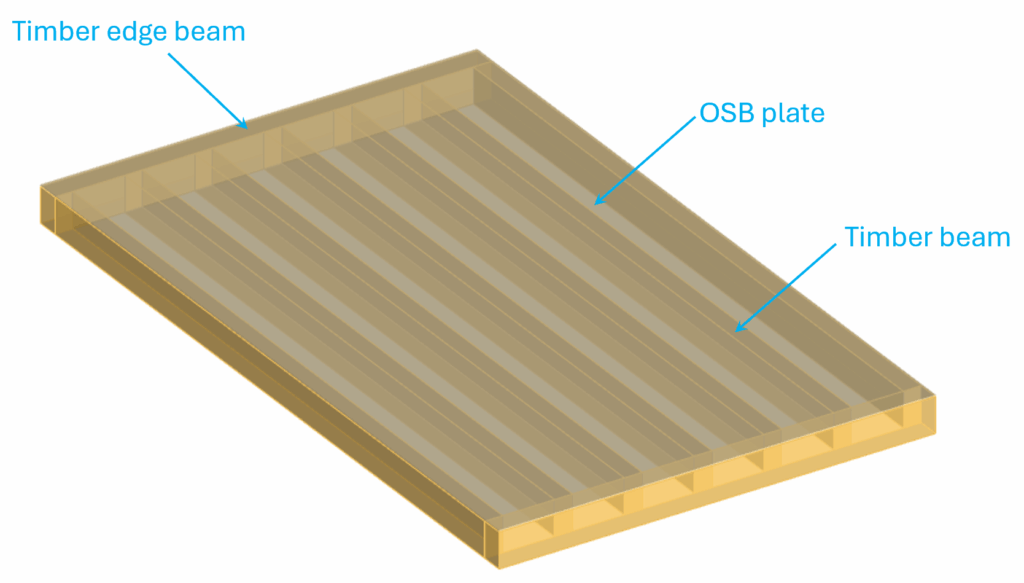
First, let’s look at an example timber floor, we are using to explain vibration analysis.
The timber joist ceiling consists of the main timber beams which connect to the edge beams. These edge beams are either supported by walls or columns. To distribute the loads to the timber beams, OSB plates are used.
Step #1: Define the material properties of the timber element
The main element we need for the vibration analysis is the main timber beams. In this tutorial, we’ll use GL28h as the timber material.
We summarized all timber materials as a blogpost (click here).
Here are the strength and stiffness properties of GL28h.
| Strength values in MPa | GL28h | |
|---|---|---|
| Bending strength | fm.g.k | 28 |
| Tensile strength parallel to grain | ft.0.g.k | 22.3 |
| Tensile strength perpendicular to grain | ft.90.g.k | 0.5 |
| Compressive strength parallel to grain | fc.0.g.k | 28 |
| Compressive strength perpendicular to grain | fc.90.g.k | 2.5 |
| Shear strength | fv.g.k | 3.5 |
| Modulus of elasticity | E0.g.mean | 12600 |
| E0.g.05 | 10500 | |
| Shear modulus | Gg.mean | 650 |
| Gg.05 | 540 | |
| Density in kg/m3 | ||
| ρg.k | 425 | |
| ρg.mean | 460 |
Step #2: Define the geometrical properties of the timber beam
The beam has the following cross-sectional properties:
- Cross-sectional height h=32cm
- Cross-sectional width w=16cm
- Moment of inertia strong axis Iy = (w ⋅ h3)/12 = 4.37 ⋅ 108 mm4
- Span l=5.7m
- Spacing of the timber beams s=62.5cm
Step #3: Calculation and verification of the fundamental frequency
First, we calculate the fundamental frequency of our floor.
There’s a little problem at the moment. Eurocode (EN 1995-1-1 7.3) gives only recommendations of vibration requirements for residential floors.
Why is this a problem? Because there is no binding document that defines the requirement for all other building types.
Let’s say you design a school with a timber floor, and you use the requirement for residential buildings from Eurocode. Now suddenly after the building is constructed a school boy or girl or a teacher feels unwell because of the vibrations.
You as the structural engineer / engineering firm could be made responsible for it.
So guys, always always always tell the client what vibration limits you use and let them confirm it in an email or document.
According to EN 1995-1-1 7.3.3 special investigations should be made if the fundamental frequency is less than 8 Hz for residential floors (my recommendation to you: design your residential floors for > 8 Hz).
So let’s first calculate the fundamental frequency (EN 1995-1-1 (7.5)).
Bending stiffness in the direction of the span:
EIl=E0.g.05 ⋅ Iy/s = 7340 kNm
Self-weight of the beams:
gk.b = ρg.k ⋅ h ⋅ w ⋅ 1/s = 34.8 kg/m2
Additional floor load (screed, OSB, etc.):
gk.a = 200 kg/m2
Total mass of the floor:
m = gk.b + gk.a = 234.8 kg/m2
Fundamental frequency (EN 1995-1-1 (7.5)):
f1 = π/(2⋅l2) ⋅ √(EIl/m) = 8.55 Hz > 8 Hz
You see that we fullfill the requirement of > 8 Hz, but changing the span to 6m would lead to a value < 8 Hz.
The span is included in the formula with ^2 which will reduce the frequency significantly. For this example we use a common timber floor with very common dead loads, which shows that spans of > 6m will be a challenge.
Next we’ll calculate the deflection of the floor due to a point load of 1 kN (EN 1995-1-1 (7.3):
Md = pd ⋅ s2/8 = 12.5 kNm
The design normal force is 0 kN:
a = (1 ⋅ l3)/(48 ⋅ EIl ⋅ bw) = 0.175 mm/kN
With bw = 3m as the width of the floor element (you could also optimize this as the room width).
Note that we’ll do the verification according to Eurocode. There might be different verifications in your National Annex. In Germany, we have different limit values defined for a (0.5 mm and 1mm for 2 kN depending on the building type). In Denmark (as far as I know) you only need to verify the frequency.
Number of first-order modes with natural frequencies up to 40 Hz (EN 1995-1-1 (7.7)):
n40 = (((40/f1)2 – 1) ⋅ (bw/l)4 ⋅ EIl/EIb)0.25 = 10.4
With EIb = 1 kNm (on the safe side to not account for any transverse stiffness, the OSB boards have a very small stiffness compared to the timber beams, also we can’t define EIb = 0 kNm as we devide through EIb later in the calc.
Floor vibration velocity EN1995-1-1 (7.6):
ν = (4 ⋅ (0.4 + 0.6 ⋅ n40))/(m ⋅ bw ⋅ l + 200) = 0.0063 m/Ns2
Dimensionless factor (Schänzlin, 2024):
b = -48.089 ⋅ ln(a) + 116.6 = 200.36
Modal damping ratio (Schänzlin, 2024):
ζ = 0.01
Check EN1995-1-1 (7.4):
ν ≤ bf1⋅ζ-1 = 1 → Fullfilled!
Final words
Alright, verifying timber floors for vibrations is not trivial. But vibration analysis is becoming more and more common as we are building more with timber and other light materials like steel.
I hope this helped.
Let’s design better structures together,
Laurin.
If you don’t want to miss any new structural design tutorials, then subscribe to our free weekly newsletter.
Or subscribe to my YouTube channel for regular updates.
Let’s design better structures together,
Laurin.

Laurin Ernst