Statik Eines Holzbalkens [Schritt für Schritt Anleitung]

Holzbalken werden viel im Hochbau, wie zum Beispiel in Decken, Dächern, Garagen, etc., verwendet. In diesem Blog-Post lernst Du, wie man die Statik eines Holzbalkens berechnet.

Als Beispiel verwenden wir den Holzträger eines Flachdachs. 👇👇

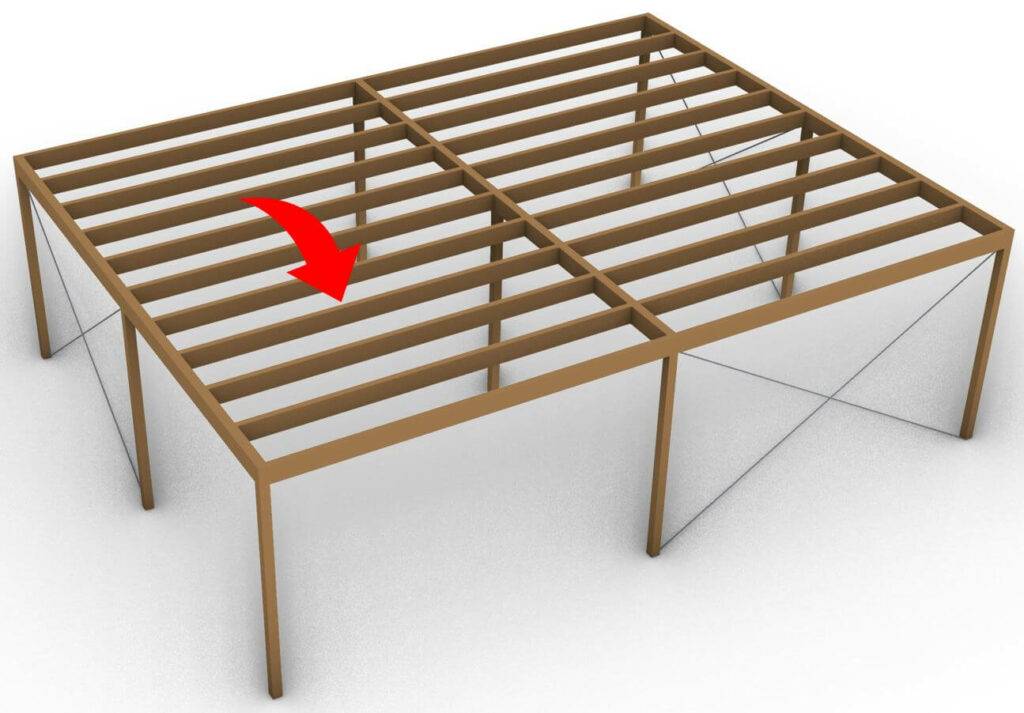
Lasst uns starten. 🚀🚀

Vorgang Holzbalken Bemessung

Statisches System

Bevor wir mit der Berechnung starten, müssen wir zuerst das statische System des Holzbalkens definieren. In den meisten Fällen werden Einfeldträger im Holzbau verwendet.

Einfeldträger haben ein Loslager und ein Festlager. 👇👇

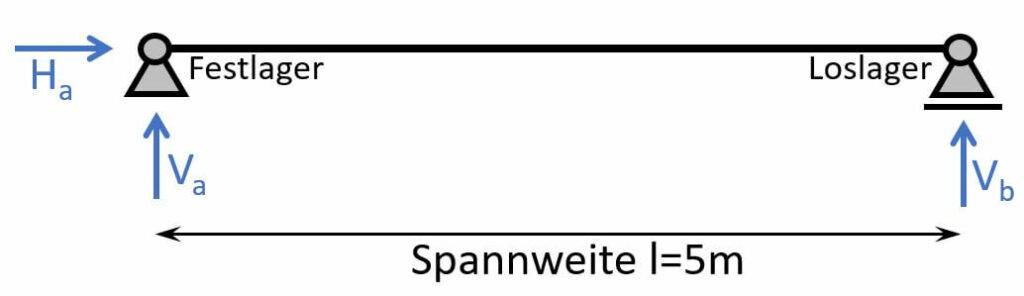
Ein Festlager hat 2 Auflagerkräfte und ein Loslager 1.

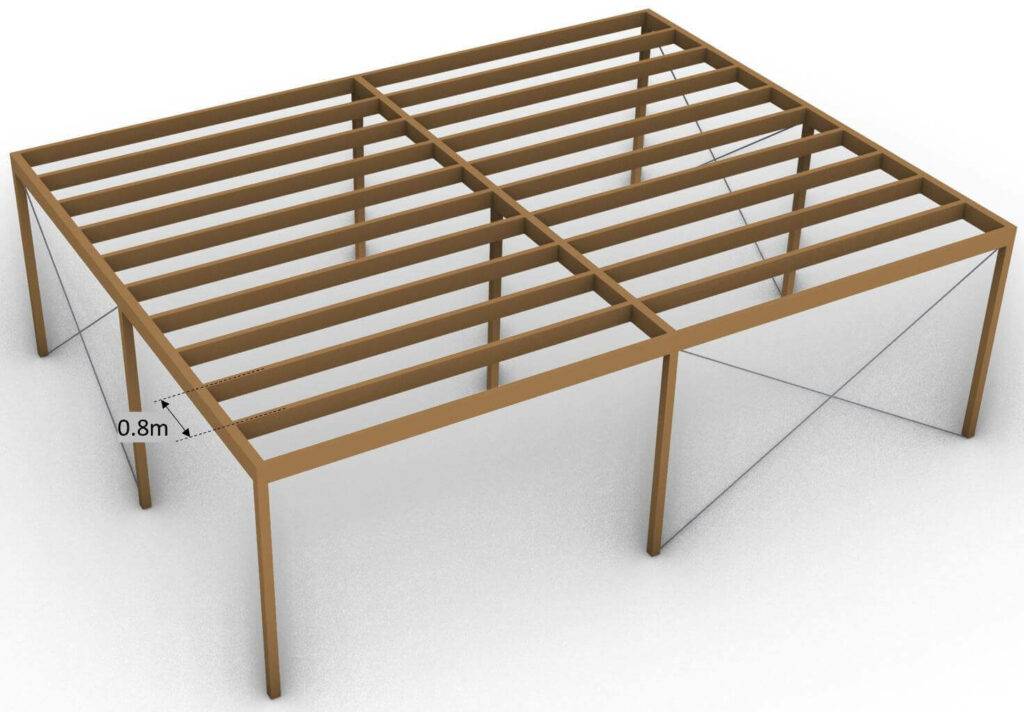
Ein Beispiel eines Holzbalkens der als Einfeldträger gerechnet wird, sind die Träger eines Flachdachs/Carports, wie im nächsten Bild.

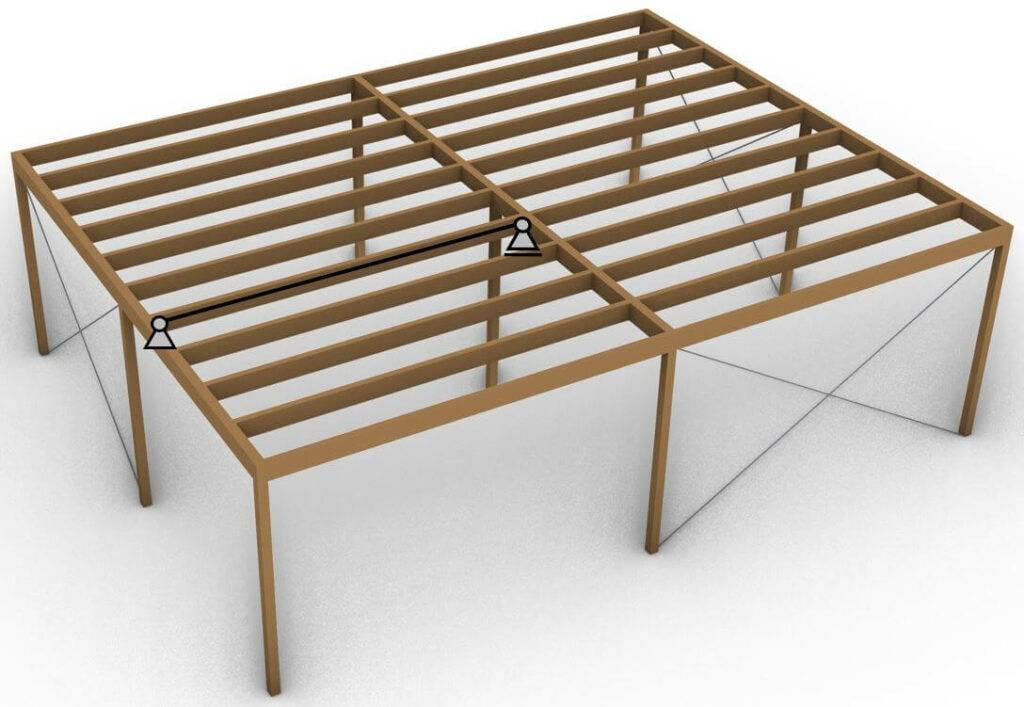
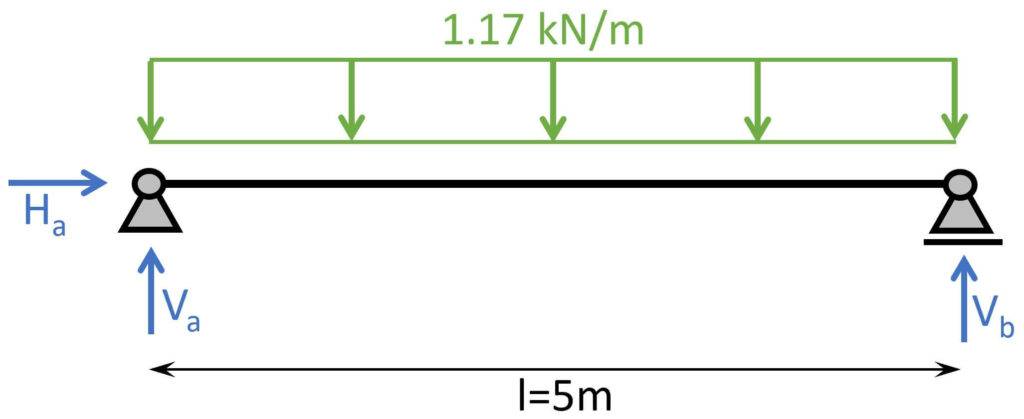
Wenn wir einen Schnitt durch das Dach mache, sieht das ganze folgendermaßen in 2D aus.

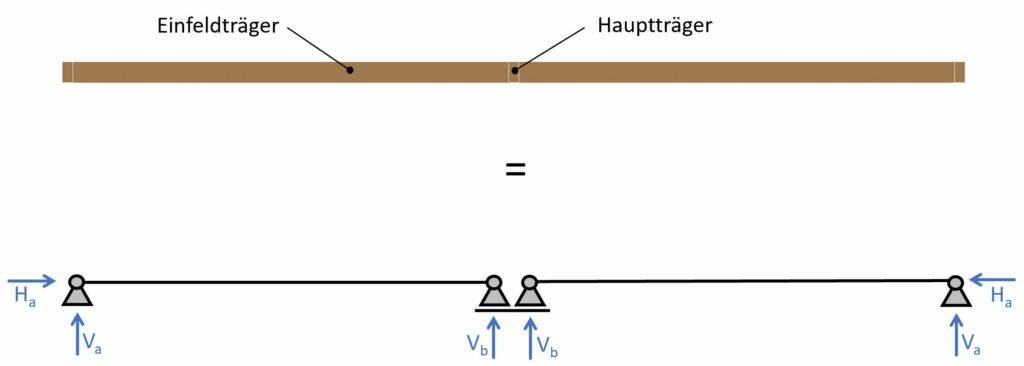
Lasten

Schnee-, Wind-, Eigen- und Nutzlast werden nach Eurocode EN 1991 gerechnet. Wir haben sehr detaillierte Artikel geschrieben, die Schritt für Schritt die Berechnung zeigen:

• Windlast eines Flachdachs
• Sneelast
• Eigenlast Berechnung
• Nutzlast

In diesem Artikel werden wir folgende Lasten annehmen. ⬇️↘️

$g_{k}$	1.08 kN/m2	Charakteristische Eigenlast
$q_{k}$	1.0 kN/m2	Charakteristische Nutzlast
$s_{k}$	1.0 kN/m2	Charakteristische Schneelast
$w_{k}$	– 1.0 kN/m2	Charakteristische Windlast

Last Kombinationen

Last Kombinationen kombinieren die einzelnen Lasten miteinander, da es oft Situationen gibt, in denen mehrere Lasten auf einmal wirken. Zusätzlich werden Sicherheitsfaktoren dazugerechnet.

Wenn du mehr über Lastkombinationen wissen willst, dann check unseren Blog post aus.

ULS Last Kombinationen

LK1	$1.35 \cdot 1.08 \frac{kN}{m^2} $	$1.46 \frac{kN}{m^2}$
LK2	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2}$	$2.96 \frac{kN}{m^2} $
LK3	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2}$	$4.0 \frac{kN}{m^2}$
LK4	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2}$	$2.96 \frac{kN}{m^2} $
LK5	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$3.1 \frac{kN}{m^2}$
LK6	$1.35 \cdot 1.08 \frac{kN}{m^2} + \Psi_{0} \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$2.1 \frac{kN}{m^2} $
LK7	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$1.0 \frac{kN}{m^2}$
LK8	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} $	$ 2.96 \frac{kN}{m^2} $
LK9	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$ -0.04 \frac{kN}{m^2} $
LK10	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$ 2.06 \frac{kN}{m^2}$
LK11	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot (-1.0 \frac{kN}{m^2}) + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} $	$1.0 \frac{kN}{m^2}$
LK12	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2})$	$2.06 \frac{kN}{m^2}$

SLS Charakteristische Last Kombinationen

LK1	$1.08 \frac{kN}{m^2} $	$1.08 \frac{kN}{m^2}$
LK2	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$	$2.08 \frac{kN}{m^2}$
LK3	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2}$	$2.78 \frac{kN}{m^2}$
LK4	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2})$	$1.48 \frac{kN}{m^2}$
LK5	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2}) $	$2.18 \frac{kN}{m^2}$
LK6	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2}) $	$1.48 \frac{kN}{m^2}$
LK7	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2}) $	$0.78 \frac{kN}{m^2}$
LK8	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$	$2.08 \frac{kN}{m^2}$
LK9	$1.08 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2}) $	$0.08 \frac{kN}{m^2}$
LK10	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2}) $	$1.48 \frac{kN}{m^2}$
LK11	$1.08 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2}) + 0.7 \cdot 1.0 \frac{kN}{m^2} $	$0.78 \frac{kN}{m^2}$
LK12	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$	$2.08 \frac{kN}{m^2}$
LK13	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2})$	$0.08 \frac{kN}{m^2}$

Holz Eigenschaften

Als Erstes muss der Statiker zwischen Konstruktionsholz und Brettschichtholz (Glulam) wählen.

Welche der Planer wählt, hängt vom Projekt, den Spannweiten, den Kosten und dem persönlichen Geschmack ab.

Für unser Balkenbeispiel verwenden wir ein Konstruktionsholz C24.

Nun müssen die Eigenschaften des Holzes C24 gefunden werden. Entweder findet man sie im Eurocode oder man sucht online nach einem Hersteller, der Tabellen mit seinen Holzprodukten bereitstellt.

Wir haben einen C24-Balken von einem Hersteller mit den folgenden Eigenschaften online gefunden.

Biegefestigkeit $f_{m.k}$	24 $\frac{N}{mm^2}$
Zugfestigkeit parallel zur Faser $f_{t.0.k}$	14 $\frac{N}{mm^2}$
Zugfestigkeit rechtwinklig zur Faser $f_{t.90.k}$	0.4 $\frac{N}{mm^2}$
Druckfestigkeit parallel zur Faser $f_{c.0.k}$	21 $\frac{N}{mm^2}$
Druckfestigkeit rechtwinklig zur Faser $f_{c.90.k}$	2.7 $\frac{N}{mm^2}$
Schubfestigkeit $f_{v.k}$	2.0 $\frac{N}{mm^2}$
E-Modul $E_{0.mean}$	11.0 $\frac{kN}{mm^2}$

K_mod Faktor

K_mod ist ein Faktor der auch mit in die Bemessung und Berechnung eines Holzbalkens miteingeht.

Der k_mod Faktor (Modifikationsfakor) berücksichtigt die Auswirkungen des Feuchtigkeitsgehaltes und der Belastungsdauer auf die Eigenschaften des Holzes.

Dieser Faktor wird zur Berechnung der Bemessungsspannungen in Holzelementen verwendet.

Der Feuchtigkeitsgehalt wird in 3 Kategorien oder sogenannte Nutzungsklassen eingeteilt.

Diese Nutzungsklassen drücken aus, wie stark ein Holzbauteil der Feuchtigkeit ausgesetzt ist, d. h. ein Bauteil, das dem Regen ausgesetzt ist, wird in Nutzungsklasse 3 eingestuft, während ein Bauteil im Inneren eines Gebäudes in Nutzungsklasse 1 eingestuft wird.

Die ausführliche Beschreibung kannst du in EN 1995-1-1 2.3.1.3 finden.

Klassen der Lasteinwirkungsdauer geben an, wie lange eine Last auf ein Tragwerk einwirkt. Je länger, desto größer der Reduktionsfaktor der Holzeigenschaften.

Die Eigenlast als Beispiel wirkt dauerhaft auf ein Bauwerk, während die Windlast nur für kurze Zeit einwirkt und daher als Kurzzeitlast eingestuft werden kann.

Die Lasteinwirkungsdauer-Klassen sind in EN 1995-1-1 Tabelle 2.2 zu finden.

In unserem Fall gehen wir nun davon aus, dass wir ein Flachdach eines Wohnhauses konstruieren. Die Balken sind nicht der Witterung ausgesetzt. Daher haben wir die Nutzungsklasse 1.

Darüber hinaus können wir auch die Belastungsdauer der Lasten, die auf unser Flachdach einwirken, gemäß EN 1995-1-1 Tabelle 2.2 definieren.

Eigenlast	Ständig
Nutzlast	Mittel
Schnee- und Windlast	Kurz

Jetzt können wir die Werte für k_mod und Konstruktionsholz C24 mithilfe EN 1995-1-1 Tabelle 3.1 ermitteln.

			kmod
Eigenlast	Stöndige Einwirkung	Nutzungsklasse 1	0.6
Nutzlast	Mittlere Einwirkung	Nutzungsklasse 1	0.8
Schnee- und Windlast	Kurze Einwirkung	Nutzungsklasse 1	0.9

Teilsicherheitsbeiwert

Der Teilsicherheitsfaktor berücksichtigt Materialeigenschaften in ULS. EN 1995-1-1 Tabelle 2.3 enthält empfohlene Faktoren.

In our case for solid timber, we get the partial factor of

In unserem Fall mit Konstruktionsholz, ist der Sicherheitsbeiwert:

$$\gamma_{M} = 1.3$$

Definition der Querschnittshöhe und -breite

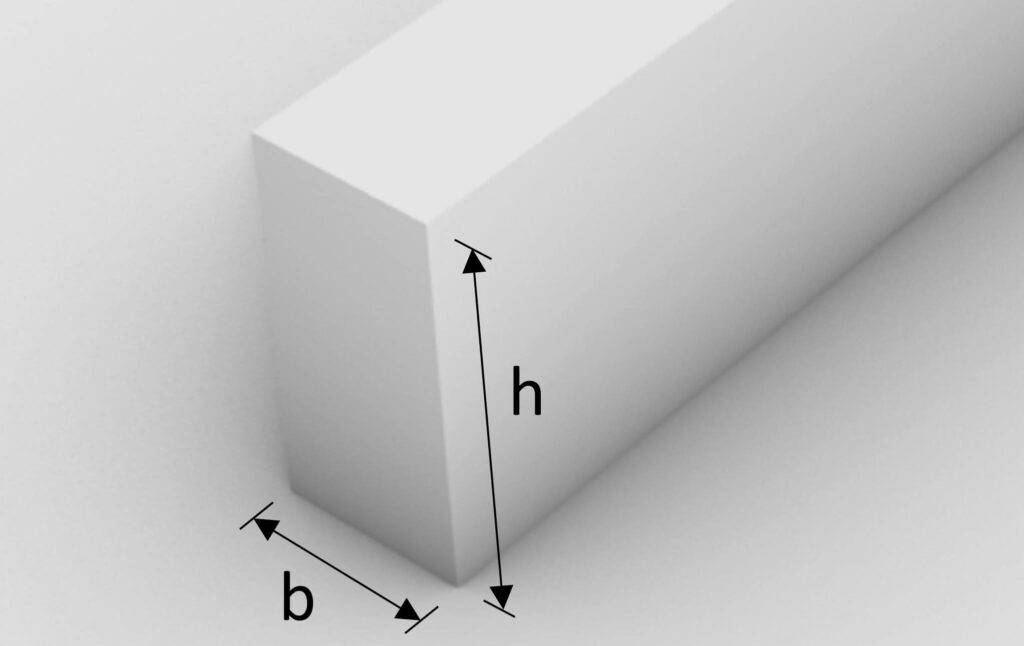
Bevor wir nun endlich mit der Statik des Trägers beginnen können, müssen wir die Breite und Höhe des Querschnitts festlegen. Dies beruht auf der Erfahrung des Statikers.

Breite b = 80 mm
Höhe h = 240 mm

Wenn wir die Höhe und Breite des Querschnitts kennen, können wir das Trägheitsmoment der starken Achse berechnen, das für die Berechnung der Biegespannung erforderlich ist.

$$I_{y} = \frac{b \cdot h^3}{12} = \frac{80mm \cdot (240mm)^3}{12} = 9.22 \cdot 10^7 mm^4 $$

ULS Nachweise

Bei der ULS (ultimate limit state) Bemessung werden die Spannungen im Holzträger aufgrund von Biegemoment und Querkraft nachgewiesen.

Bevor wir mit den Berechnungen beginnen, müssen wir die ungünstigsten Lastkombinationen für ständige, mittelfristige und kurzzeitige Einwirkungen auswählen, d.h. die höchsten Lasten, da diese Einwirkungen aufgrund unterschiedlicher $k_{mod}$-Werte zu unterschiedlichen Widerstandsspannungen führen.

LK1 (Ständig)	$1.35 \cdot 1.08 \frac{kN}{m^2} $	$1.46 \frac{kN}{m^2}$
LK3 (Mittel)	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2}$	$4.0 \frac{kN}{m^2}$
LK5 (Kurz)	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$3.1 \frac{kN}{m^2}$

Da wir die Träger in 2D nachweisen werden, müssen wir die Flächenlasten (kN/m²) in Linienlasten (kN/m) umwandeln.

Wir erhalten die Linienlast dadurch, dass wir die Flächenlast mit dem Balkenabstand multiplizieren.

LK1 (Ständig)	$1.46 \frac{kN}{m^2} \cdot 0.8m $	$1.17 \frac{kN}{m} $
LK3 (Mittel)	$4.0 \frac{kN}{m^2} \cdot 0.8m $	$3.2 \frac{kN}{m} $
LK5 (Kurz)	$3.1 \frac{kN}{m^2} \cdot 0.8m $	$2.48 \frac{kN}{m} $

Diese Streckenlasten können nun auf unser statisches System angesetzt werden. Als Beispiel verwenden wir die Last von LK1 an.

Biegung

Aus den 3 kritischen Lastkombinationen LK1, LK3 und LK5 können wir nun das Biegemoment berechnen.

Das größte Biegemoment in einem Einfeldträger befindet sich in der Mitte der Spannweite und kann mit der folgenden Formel berechnet werden:

$$M_{d} = q \cdot \frac{l^2}{8}$$

Mit

• $q$ der Linienlast die auf den Träger wirkt
• $L$ der Spannweite

Dies ergibt die folgende Biegemomente der kritischen Lastkombinationen.

LK1	$1.17 \frac{kN}{m} \cdot \frac{(5m)^2}{8} $	$3.66 kNm $
LK3	$3.2 \frac{kN}{m} \cdot \frac{(5m)^2}{8} $	$10 kNm $
LK5	$2.48 \frac{kN}{m} \cdot \frac{(5m)^2}{8} $	$7.75 kNm $

Mit dem Biegemoment lässt sich die Spannung im kritischsten Punkt des Querschnitt (bei Einfeldträger in der Mitte der Spannweite) berechnen.

$$\sigma = \frac{M_{d}}{I_{y}} \cdot \frac{h}{2}$$

LK1	$\frac{3.66 kNm}{9.22 \cdot 10^7 mm^4} \cdot \frac{0.24m}{2} $	$4.76 MPa $
LK3	$\frac{10 kNm}{9.22 \cdot 10^7 mm^4} \cdot \frac{0.24m}{2} $	$13.0 MPa $
LK5	$\frac{7.75 kNm}{9.22 \cdot 10^7 mm^4} \cdot \frac{0.24m}{2} $	$10.1 MPa $

Als nächstes berechnen wir die Widerstandsspannungen des Holzmaterials.

$$ f_{m.d} = k_{mod} \cdot \frac{f_{m.k}}{\gamma_{m}} $$

LK1	$k_{mod} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$0.6 \cdot \frac{24 MPa}{1.3} $	$11.1 MPa $
LK3	$k_{mod} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$0.8 \cdot \frac{24 MPa}{1.3} $	$14.77 MPa $
LK5	$k_{mod} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$0.9 \cdot \frac{24 MPa}{1.3} $	$16.6 MPa $

Nun können wir die Ausnutzung des Querschnitts berechnen.

$$\eta = \frac{\sigma}{f_{m.d}}$$

LK1 (Ständig)	$\frac{\sigma}{f_{m.d}} $	$\frac{4.76 MPa}{11.1 MPa} $	$ 0.43 $
LC3 (Mittel)	$\frac{\sigma}{f_{m.d}} $	$\frac{13 MPa}{14.77 MPa} $	$ 0.88 $
LC5 (Kurz)	$\frac{\sigma}{f_{m.d}} $	$\frac{10.1 MPa}{16.6 MPa} $	$ 0.61 $

Schub

Wie bei Biegung berechnen wir die Querkraft anhand der 3 kritischen Lastkombinationen LK1, LK3 und LK5. Die höchste Querkraft in einem Einfeldträger befindet sich an den Auflagern und kann mit der folgenden Formel berechnet werden:

$$V_{d} = q \cdot \frac{L}{2}$$

Mit

• $q$ der Linienlast, die auf den Balken wirkt und
• $L$ der Spannweite

Daraus ergeben sich die folgenden Querkräfte für LK1, LK3 und LK5

LK1 (Ständig)	$1.17 \frac{kN}{m} \cdot \frac{5m}{2} $	$2.93 kN $
LK3 (Mittel)	$3.2 \frac{kN}{m} \cdot \frac{5m}{2} $	$8 kN $
LK5 (Kurz)	$2.48 \frac{kN}{m} \cdot \frac{5m}{2} $	$6.2 kN $

Aus den Querkräften berechnen wir die Spannung an der kritischsten Stelle im Querschnitt (in der Nähe des Auflagers bei Einfeldträgern).

$$\tau = \frac{3}{2} \cdot \frac{V_{d}}{b \cdot h} $$

LK1	$\frac{3}{2} \cdot \frac{2.93 kN}{0.08m \cdot 0.24m} $	$0.23 MPa $
LK3	$\frac{3}{2} \cdot \frac{8 kN}{0.08m \cdot 0.24m} $	$0.63 MPa $
LK5	$\frac{3}{2} \cdot \frac{6.2 kN}{0.08m \cdot 0.24m} $	$0.48 MPa $

Jetzt berechnen wir die Scherfestigkeitsspannungen des Holzes C24.

$$f_{v.d} = k_{mod} \cdot \frac{f_{v.k}}{\gamma_{m}}$$

LK1 (Ständig)	$k_{mod} \cdot \frac{f_{v.k}}{\gamma_{m}} $	$0.6 \cdot \frac{4 MPa}{1.3} $	$1.85 MPa $
LK3 (Mittel)	$k_{mod} \cdot \frac{f_{v.k}}{\gamma_{m}} $	$0.8 \cdot \frac{4 MPa}{1.3} $	$2.46 MPa $
LK5 (Kurz)	$k_{mod} \cdot \frac{f_{v.k}}{\gamma_{m}} $	$0.9 \cdot \frac{4 MPa}{1.3} $	$2.8 MPa $

Schließlich können wir die Auslastung des Querschnitts an seinem kritischsten Punkt berechnen.

$$\eta = \frac{\tau}{f_{v.d}}$$

LK1 (Ständig)	$\frac{\tau.P}{f_{v.d.P}} $	$\frac{0.23 MPa}{1.85 MPa} $	$ 0.124 $
LK3 (Mittel)	$\frac{\tau.L}{f_{v.d.L}} $	$\frac{0.63 MPa}{2.46 MPa} $	$ 0.25 $
LK5 (Kurz)	$\frac{\tau.I}{f_{v.d.I}} $	$\frac{0.48 MPa}{2.8 MPa} $	$ 0.17 $

SLS Bemessung

Durchbiegung

Bevor wir mit den Berechnungen beginnen, müssen wir einige Parameter aus EN 1995-1-1 Abbildung 7.1 definieren:

• $w_{c}$ = Überhöhung
• $w_{inst}$ = unmittelbare Durchbiegung (instanteneous deflection)
• $w_{creep}$ = Kriechdurchbiegung (creep deflection)
• $w_{fin}$ = Enddurchbiegung $w_{inst} + w_{creep}$
• $w_{net.fin}$ = Netto Enddurchbiegung $w_{inst} + w_{creep} – w_{c}$

EN 1995-1-1 Table 7.2 recommends values for $w_{inst}, w_{net.fin}$ and $w_{fin}$ which should not be exceeded for a simply supported beam.

EN 1995-1-1 Tabelle 7.2 empfiehlt Werte für w_inst, w_net.fin und w_fin, die für einen Einfeldträger nicht überschritten werden sollten.

$w_{inst}$	$w_{net.fin}$	$w_{fin}$
$L/300$ – $L/500$	$L/250$ – $L/350 $	$L/150$ – $L/300 $

Mit einer Trägerlänge von L=5m bekommen wir folgende Werte: 👇👇

$w_{inst}$	$w_{net.fin}$	$w_{fin}$
16.67mm bis 10mm	20mm bis 14.3mm	33.3mm bis 16.67mm

Unmittelbare Durchbiegung u_inst

$u_{inst}$ (instantaneous deformation) of our beam can be calculated with the load of the characteristic loadcombination. Looking at all loadcombinations we can see that LC3 leads to the biggest load where the live load is the leading and the snow load the accompanying variable action.

u_inst (unmittelbare bzw. sofortige Durchbiegung) unseres Trägers kann mit der Last der charakteristischen Lastkombination berechnet werden. Betrachtet man alle Lastkombinationen, so stellt man fest, dass LK3 zur größten Last führt, wobei die Nutzlast die dominierende und die Schneelast die begleitende veränderliche Einwirkung ist.

LC3

$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2}$

$2.78 \frac{kN}{m^2}$

Die Umwandlung dieser Last in eine Linienlast ergibt:

$$2.78 \frac{kN}{m^2} \cdot 0.8m = 2.22 \frac{kN}{m}$$

Which we now can put in the deflection formula for line loads on simply supported beams.

Diese können wir nun in die Formel für Linienlasten auf Einfeldträgern einsetzen.

$$u_{inst} = \frac{5}{384} \cdot q \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} $$

$$u_{inst} = \frac{5}{384} \cdot 2.22 \frac{kN}{m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 9.22 \cdot 10^7 mm^4} = 17.85mm$$

Nun können wir die Auslastung überprüfen.

$$\eta = \frac{u_{inst}}{w_{inst}}$$

$$\eta = \frac{17.85mm}{16.67mm} = 1.07$$

Erhöhung der Querschnittsparameter

Breite b = 100 mm
Höhe h = 240 mm
Trägheitsmoment $I_{y} = 1.15 \cdot 10^8 mm^4 $

Jetzt führen wir die Durchbiegungsberechnung erneut mit den aktualisierten Abmessungen durch.

$$ \frac{5}{384} \cdot 2.22 \frac{kN}{m}  \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4} = 14.28mm$$

Auslastung. 👇👇

$$\eta = \frac{14.28mm}{16.67mm} = 0.85$$

Gesamt Durchbiegung $u_{fin}$

$u_{fin}$ (Endverformung) unseres Trägers wird damit berechnet dass wir die Kriechverformung $u_{creep}$ zur unmittelbaren Durchbiegung $u_{inst}$ dazurechnen. Deshalb schauen wir uns jetzt an, wie wir die Kriechverformung von LK3 berechnen.

Kriechverformung:

$$u_{creep.g} = u_{inst.g} \cdot k_{def} $$
$$u_{creep.g} = \frac{5}{384} \cdot g_{k} \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} \cdot k_{def}$$

Mit ⬇️⬇️

$k_{def} $ = 0.6 für Konstruktionsholz der Nutzungsklasse 1 (EN 1995-1-1)

$$u_{creep.g} = \frac{5}{384} \cdot 0.86 \frac{kN/m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4 } \cdot 0.6$$
$$u_{creep.g} = 3.33 mm$$

Die Kriechverformung aufgrund der dominierenden variablen Einwirkung (in unserem Fall die Nutzlast LK3) wird wie folgt berechnet:

$$u_{creep.q} = u_{inst.q} \cdot k_{def} \cdot \Psi_{2.q} $$
$$u_{creep.q} = \frac{5}{384} \cdot q_{k} \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} \cdot k_{def} \cdot \Psi_{2.q}$$

Mit

$\Psi_{2.q}$ = 0 für Nutzlasten auf Dächer (EN 1990 Tabelle A1.1)

$u_{creep.q} = \frac{5}{384} \cdot 0.8 \frac{kN/m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4 } \cdot 0.6 \cdot 0$
$u_{creep.q} = 0$

Die Kriechverformung aufgrund der begleitenden veränderlichen Einwirkung (in unserem Fall Schneelast – LK3) wird berechnet als:

$$u_{creep.s} = u_{inst.s} \cdot k_{def} \cdot \Psi_{2.s} $$
$$u_{creep.s} = \frac{5}{384} \cdot q_{k} \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} \cdot k_{def} \cdot \Psi_{2.s}$$

Mit

$\Psi_{2.s} $ = 0.2 für Schweden (EN 1990 Tabelle A1.1)

$$u_{creep.s} = \frac{5}{384} \cdot 0.8 \frac{kN/m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4 } \cdot 0.6 \cdot 0.2$$
$$u_{creep.s} = 0.43 mm$$

Adding the creep to the instantaneous deflection leads to the final deflection.

Addiert man die Kriechdurchbiegung zur unmittelbaren Durchbiegung, erhält man die Gesamtdurchbiegung.

$$u_{fin} = u_{inst} + u_{creep.g} + u_{creep.q} + u_{creep.s}$$

$$u_{fin} = 14.28mm + 3.33mm + 0mm + 0.43mm = 18.04mm$$

Das führt zu einer Auslastung von:

$$\eta = \frac{18.04mm}{33.3mm} = 0.54$$