Timber Beam Design [Step-By-Step]

Wooden beams are used a lot in structural engineering, such as ceilings, roofs, garages, etc. In this blog post you will learn how to calculate the statics of a wooden beam.

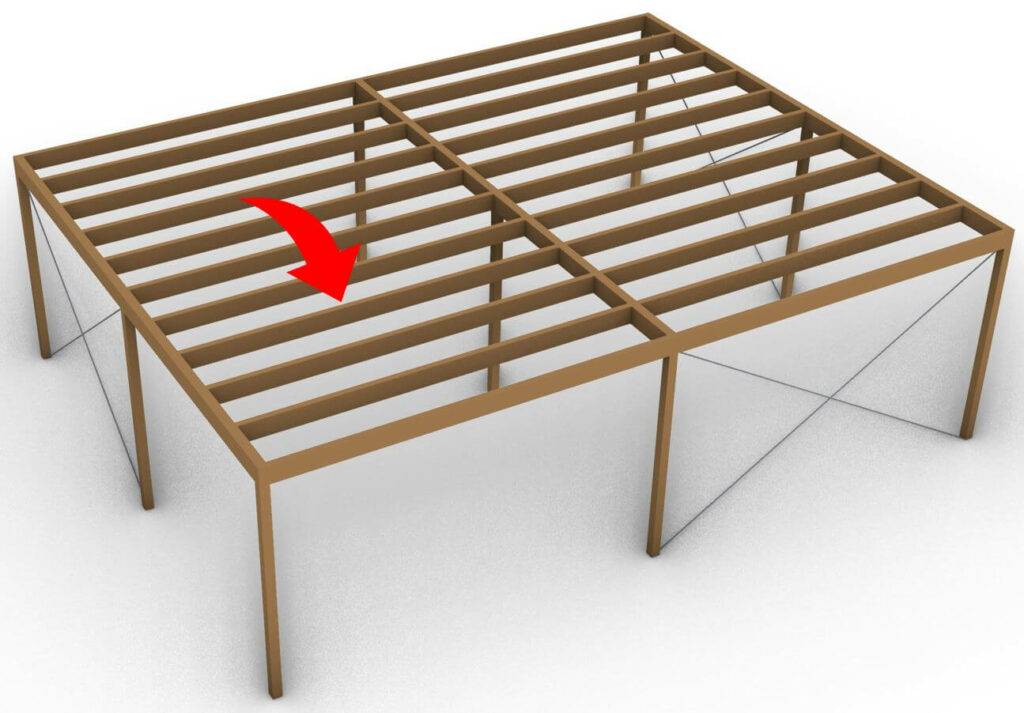
We will use the wooden beam of a flat roof as an example. 👇👇

Let’s get started. 🚀🚀

Process Of Calculating A Timber Beam

Static system

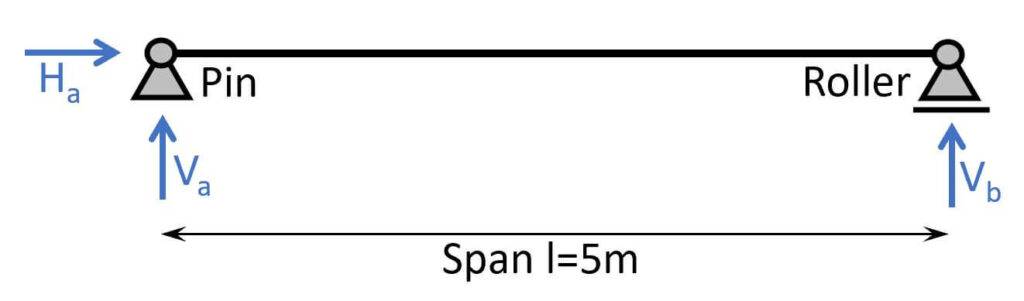
The static system of a simply supported beam can be visualized as in the next picture. It consists of one roller (takes up a vertical force V2) and one pinned support (takes up a vertical V1 and a horizontal force H1).

To keep it in context this simply supported beam can be a secondary beam in a flat roof.

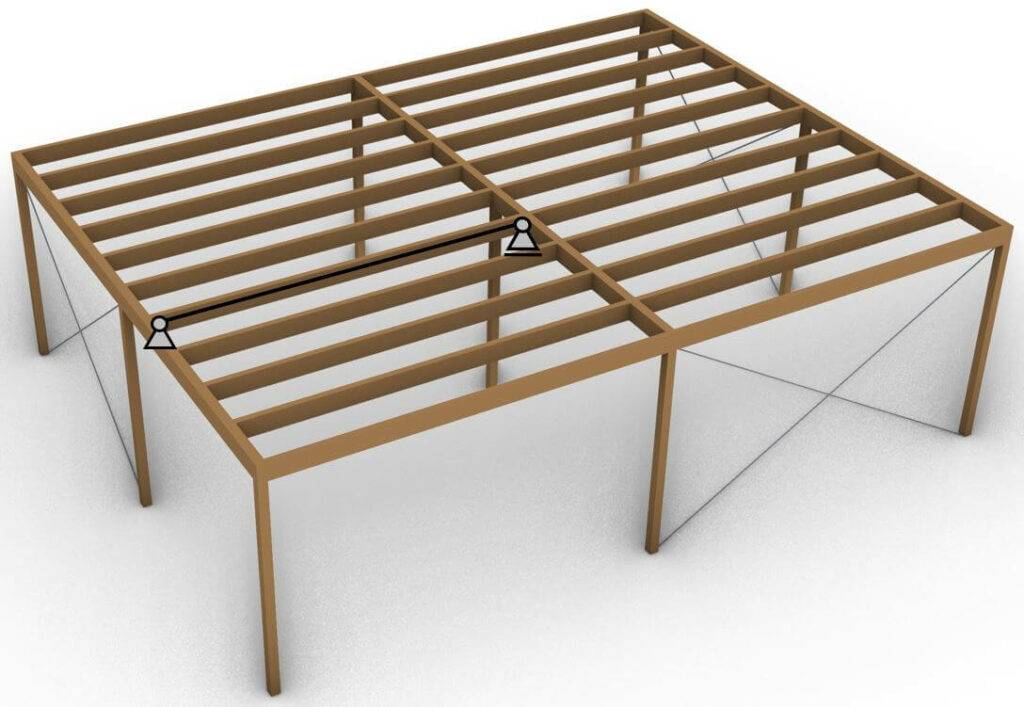
Now when we visualize the secondary beams (dashed in picture) in a 2D section we can easily compare it to the statical system.

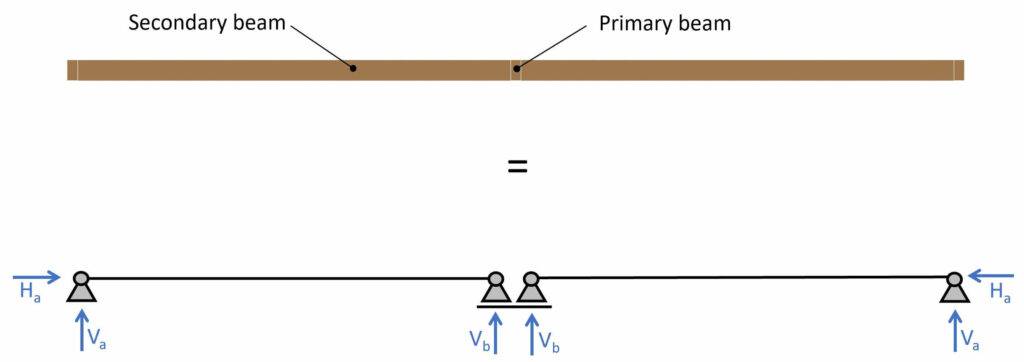
You can learn more about different timber roof types and how their statical systems work in this post.

Loads

We will use the loads that we assumed in our blog post about Load combinations. If you wanna learn more about the different types of loads, what they are and how to apply them, you can read that in this post.

$g_{k}$	1.08 kN/m2	Characteristic value of dead load
$q_{k}$	1.0 kN/m2	Characteristic value of live load
$s_{k}$	1.0 kN/m2	Characteristic value of snow load
$w_{k}$	-1.0 kN/m2	Characteristic value of wind load

Load combinations

As the basis of our calculation we will use the load combinations and loads from this blog post where we extensively explained what they are and how they work.

ULS Load combinations

LC1	$1.35 \cdot 1.08 \frac{kN}{m^2} $	$1.46 \frac{kN}{m^2}$
LC2	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2}$	$2.96 \frac{kN}{m^2} $
LC3	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2}$	$4.0 \frac{kN}{m^2}$
LC4	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2}$	$2.96 \frac{kN}{m^2} $
LC5	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$3.1 \frac{kN}{m^2}$
LC6	$1.35 \cdot 1.08 \frac{kN}{m^2} + \Psi_{0} \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$2.1 \frac{kN}{m^2} $
LC7	$1.35 \cdot 1.08 \frac{kN}{m^2} + 0 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$1.0 \frac{kN}{m^2}$
LC8	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} $	$ 2.96 \frac{kN}{m^2} $
LC9	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$ -0.04 \frac{kN}{m^2} $
LC10	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$ 2.06 \frac{kN}{m^2}$
LC11	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot (-1.0 \frac{kN}{m^2}) + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} $	$1.0 \frac{kN}{m^2}$
LC12	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 * 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2})$	$2.06 \frac{kN}{m^2}$

Characteristic SLS Load combinations

LC1	$1.08 \frac{kN}{m^2} $	$1.08 \frac{kN}{m^2}$
LC2	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$	$2.08 \frac{kN}{m^2}$
LC3	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2}$	$2.78 \frac{kN}{m^2}$
LC4	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2})$	$1.48 \frac{kN}{m^2}$
LC5	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2}) $	$2.18 \frac{kN}{m^2}$
LC6	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2}) $	$1.48 \frac{kN}{m^2}$
LC7	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.0 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2}) $	$0.78 \frac{kN}{m^2}$
LC8	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$	$2.08 \frac{kN}{m^2}$
LC9	$1.08 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2}) $	$0.08 \frac{kN}{m^2}$
LC10	$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.6 \cdot (-1.0 \frac{kN}{m^2}) $	$1.48 \frac{kN}{m^2}$
LC11	$1.08 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2}) + 0.7 \cdot 1.0 \frac{kN}{m^2} $	$0.78 \frac{kN}{m^2}$
LC12	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2}$	$2.08 \frac{kN}{m^2}$
LC13	$1.08 \frac{kN}{m^2} + 0 \cdot 1.0 \frac{kN}{m^2} + (-1.0 \frac{kN}{m^2})$	$0.08 \frac{kN}{m^2}$

Beam timber material

First, the designer needs to pick between structural wood and engineered wood, such as Glulam (Glued-laminated timber) or LVL (Laminated Veneer Lumber).

Which the designer picks depend on the project, spans, cost and the personal taste.

So for our beam example we are using a structural timber C24.

Now we need to find the properties of this timber, and we can either find it in Eurocode or we find a manufacturer online which has tables of its timber products.

We found a C24 beam from a manufacturer online with the following properties.

Bending strength $f_{m.k}$	24 $\frac{N}{mm^2}$
Tension strength parallel to grain $f_{t.0.k}$	14 $\frac{N}{mm^2}$
Tension strength perpendicular to grain $f_{t.90.k}$	0.4 $\frac{N}{mm^2}$
Compression strength parallel to grain $f_{c.0.k}$	21 $\frac{N}{mm^2}$
Compression strength perpendicular to grain $f_{c.90.k}$	2.5 $\frac{N}{mm^2}$
Shear strength $f_{v.k}$	4.0 $\frac{N}{mm^2}$
E-modulus $E_{0.mean}$	11.0 $\frac{kN}{mm^2}$

Modification factor k_mod

The modification factor $k_{mod}$ takes into account the effects of the moisture content and the load duration on the properties of the timber.

This factor will be used to calculate the design stresses in timber elements.

The moisture content is split up in 3 categories or so-called Service classes.

Those service classes express how exposed a timber element is to moisture, meaning that an element that is exposed to rain can be put in service class 3 whereas an element inside of a building can be put in service class 1.

The detailed description can be found in EN 1995-1-1 2.3.1.3.

The load duration classes express how long a load acts on a structure because the longer, the greater the reduction of the timber properties will be.

The dead load, as an example, acts on a structure permanently while a wind load acts only for a short time and therefore can be classified as an instantaneous load.

The load duration classes can be found in EN 1995-1-1 Table 2.2.

Now in our case we are assuming that we are designing a flat roof of a residential house. The beams are not exposed to weather. Therefore we have Service class 1.

Furthermore, we can also define the load duration of the loads that are acting on our flat roof according to EN 1995-1-1 Table 2.2.

Self-weight/dead load	Permanent
Live load, Snow load	Medium-term
Wind load	Instantaneous

We can now find the values of $k_{mod}$ for C24 structural wood (Solid timber) and our different loads according to EN 1995-1-1 Table 3.1

			kmod
Self-weight/dead load	Permanent action	Service class 1	0.6
Live load, Snow load	Medium term action	Service class 1	0.8
Wind load	Instantaneous action	Service class 1	1.1

Partial Factor

The partial factor $\gamma_{M}$ takes into account material properties at ULS. EN 1995-1-1 Table 2.3 represents recommended partial factors.

In our case for solid timber, we get the partial factor of

$$\gamma_{M} = 1.3$$

Assumption of width and height of beam

Before we now can finally start with the design of the beam, we need to define the width and height of the beam cross-section. This is based on the experience of the designer.

Check out this article to digitize your hand calculations.

Width w = 80 mm
Height h = 240 mm

Once we know the height and width of the cross-section we can calculate the moment of inertia of the strong axis which is needed to calculate the stress due to bending.

$I_{y} = \frac{w \cdot h^3}{12} = \frac{80mm \cdot (240mm)^3}{12} = 9.22 \cdot 10^7 mm^4 $

ULS Design

In the ULS (ultimate limit state) Design we verify the stresses in the timber members due to bending and shear.

Before we start calculating anything we need to pick out the worst case loadcombinations for permanent, medium-term and instantaneous actions meaning the highest values because those actions lead to different resistance stresses due to different $k_{mod}$ values.

LC1 (P-action)	$1.35 \cdot 1.08 \frac{kN}{m^2} $	$1.46 \frac{kN}{m^2}$
LC3 (L-action)	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2}$	$4.0 \frac{kN}{m^2}$
LC5 (I-action)	$1.35 \cdot 1.08 \frac{kN}{m^2} + 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.7 \cdot 1.5 \cdot 1.0 \frac{kN}{m^2} + 0.6 \cdot 1.5 \cdot (-1.0 \frac{kN}{m^2}) $	$3.1 \frac{kN}{m^2}$

Since we will design a beam in 2D we need to transform the area loads ($\frac{kN}{m^2}$) into line loads ($\frac{kN}{m}$). We do this by multiplication with the distance between the centerlines of 2 beams.

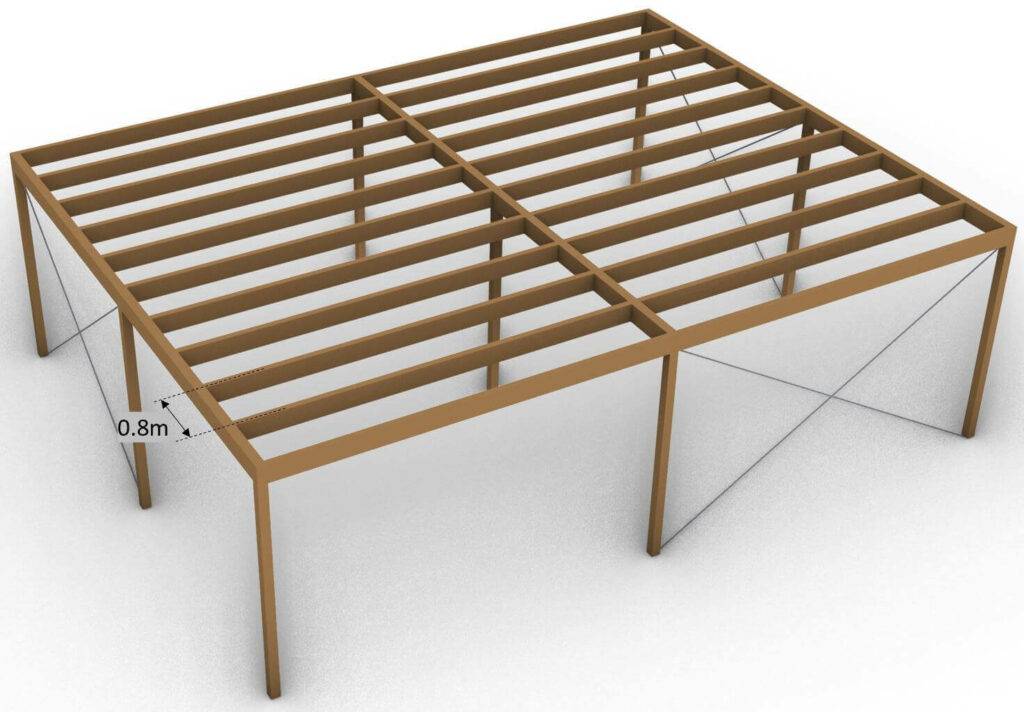
LC1 (P-action)	$1.46 \frac{kN}{m^2} \cdot 0.8m $	$1.17 \frac{kN}{m} $
LC3 (L-action)	$4.0 \frac{kN}{m^2} \cdot 0.8m $	$3.2 \frac{kN}{m} $
LC5 (I-action)	$3.1 \frac{kN}{m^2} \cdot 0.8m $	$2.48 \frac{kN}{m} $

Those line loads can now be applied to our statical system. As an example we apply the load of LC1.

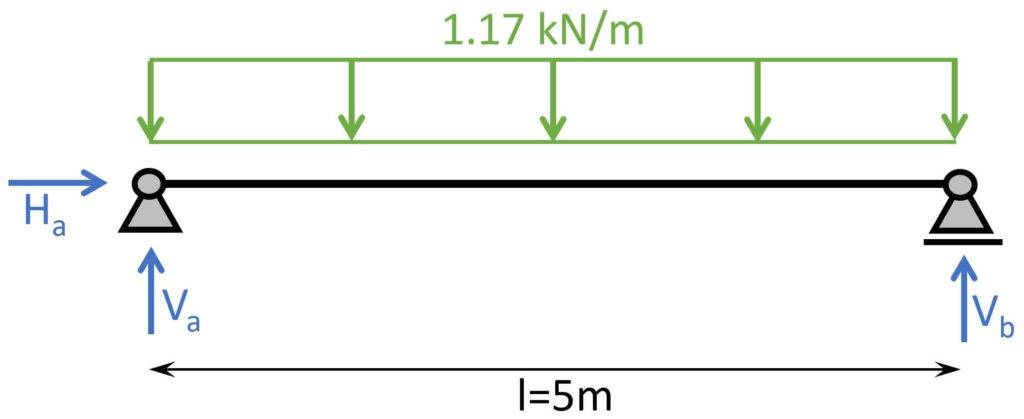
Bending

From the 3 leading Loadcombinations LC1, LC3 and LC5 we can go ahead and calculate the most critical bending moment. The highest bending moment in a simply supported beam is found in the midspan and can be calculated with the following formula:

$M_{d} = q \cdot \frac{L^2}{8}$

Where

• $q$ is the applied load on the beam
• $L$ is the span

This results in the following bending moments due to LC1, LC3 and LC5

LC1 (P-action)	$1.17 \frac{kN}{m} \cdot \frac{(5m)^2}{8} $	$3.66 kNm $
LC3 (L-action)	$3.2 \frac{kN}{m} \cdot \frac{(5m)^2}{8} $	$10 kNm $
LC5 (I-action)	$2.48 \frac{kN}{m} \cdot \frac{(5m)^2}{8} $	$7.75 kNm $

From the bending moment, we can calculate the stress in the most critical cross-section (midspan for simply supported beam).

$\sigma = \frac{M_{d}}{I_{y}} \cdot \frac{h}{2}$

LC1 (P-action)	$\frac{3.66 kNm}{9.22 \cdot 10^7 mm^4} \cdot \frac{0.24m}{2} $	$4.76 MPa $
LC3 (L-action)	$\frac{10 kNm}{9.22 \cdot 10^7 mm^4} \cdot \frac{0.24m}{2} $	$13.0 MPa $
LC5 (I-action)	$\frac{7.75 kNm}{9.22 \cdot 10^7 mm^4} \cdot \frac{0.24m}{2} $	$10.1 MPa $

The last step, before we can check whether or not the cross section can resist the loads, is calculating the Resistance stresses of the timber material.

$ f_{m.d} = k_{mod} \cdot \frac{f_{m.k}}{\gamma_{m}} $

LC1 (P-action)	$k_{mod.P} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$0.6 \cdot \frac{24 MPa}{1.3} $	$11.1 MPa $
LC3 (L-action)	$k_{mod.L} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$0.8 \cdot \frac{24 MPa}{1.3} $	$14.77 MPa $
LC5 (I-action)	$k_{mod.I} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$1.1 \cdot \frac{24 MPa}{1.3} $	$20.31 MPa $

Finally, we can calculate the utilization of the cross-section at its most critical point.

$\eta = \frac{\sigma}{f_{m.d}}$

LC1 (P-action)	$\frac{\sigma.P}{f_{m.d.P}} $	$\frac{4.76 MPa}{11.1 MPa} $	$ 0.43 $
LC3 (L-action)	$\frac{\sigma.L}{f_{m.d.L}} $	$\frac{13 MPa}{14.77 MPa} $	$ 0.88 $
LC5 (I-action)	$\frac{\sigma.I}{f_{m.d.I}} $	$\frac{10.1 MPa}{20.31 MPa} $	$ 0.5 $

Shear

Like in bending from the 3 leading load combinations LC1, LC3 and LC5 we can go ahead and calculate the most critical shear force. The highest shear force in a simply supported beam is found near the 2 supports and can be calculated with the following formula:

$$V_{d} = q * \frac{L}{2}$$

Where

• $q$ is the applied load on the beam
• $L$ is the span

This results in the following shear forces due to LC1, LC3 and LC5

LC1 (P-action)	$1.17 \frac{kN}{m} \cdot \frac{5m}{2} $	$2.93 kN $
LC3 (L-action)	$3.2 \frac{kN}{m} \cdot \frac{5m}{2} $	$8 kN $
LC5 (I-action)	$2.48 \frac{kN}{m} \cdot \frac{5m}{2} $	$6.2 kN $

From the shear forces, we can calculate the stress in the most critical cross-section (near support for simply supported beam).

$\tau = \frac{3}{2} \cdot \frac{V_{d}}{w \cdot h} $

LC1 (P-action)	$\frac{3}{2} \cdot \frac{2.93 kN}{0.08m \cdot 0.24m} $	$0.23 MPa $
LC3 (L-action)	$\frac{3}{2} \cdot \frac{8 kN}{0.08m \cdot 0.24m} $	$0.63 MPa $
LC5 (I-action)	$\frac{3}{2} \cdot \frac{6.2 kN}{0.08m \cdot 0.24m} $	$0.48 MPa $

The last step, before we can check whether the cross-section can resist the loads, is calculating the shear resistance stresses of the timber material.

$$f_{v.d} = k_{mod} * \frac{f_{v.k}}{\gamma_{m}}$$

LC1 (P-action)	$k_{mod.P} \cdot \frac{f_{v.k}}{\gamma_{m}} $	$0.6 \cdot \frac{4 MPa}{1.3} $	$1.85 MPa $
LC3 (L-action)	$k_{mod.L} \cdot \frac{f_{v.k}}{\gamma_{m}} $	$0.8 \cdot \frac{4 MPa}{1.3} $	$2.46 MPa $
LC5 (I-action)	$k_{mod.I} \cdot \frac{f_{v.k}}{\gamma_{m}} $	$1.1 \cdot \frac{4 MPa}{1.3} $	$3.39 MPa $

Finally we can calculate the utilization of the cross section at its most critical point.

$$\eta = \frac{\tau}{f_{v.d}}$$

LC1 (P-action)	$\frac{\tau.P}{f_{v.d.P}} $	$\frac{0.23 MPa}{1.85 MPa} $	$ 0.124 $
LC3 (L-action)	$\frac{\tau.L}{f_{v.d.L}} $	$\frac{0.63 MPa}{2.46 MPa} $	$ 0.25 $
LC5 (I-action)	$\frac{\tau.I}{f_{v.d.I}} $	$\frac{0.48 MPa}{3.39 MPa} $	$ 0.14 $

SLS Design

Deflection

Before we start calculating anything we need to define a few variables from EN 1995-1-1 Figure 7.1

• $w_{c}$ is the precamber
• $w_{inst}$ is the instantaneous deformation
• $w_{creep}$ is the creep deformation
• $w_{fin}$ is the final deformation: $w_{inst} + w_{creep}$
• $w_{net.fin}$ is the net final deformation: $w_{inst} + w_{creep} – w_{c}$

EN 1995-1-1 Table 7.2 recommends values for $w_{inst}, w_{net.fin}$ and $w_{fin}$ which should not be exceeded for a simply supported beam.

$w_{inst}$	$w_{net.fin}$	$w_{fin}$
$L/300$ to $L/500$	$L/250$ to $L/350 $	$L/150$ to $L/300 $

With a beam length (span) of L=5m we get the following values.

$w_{inst}$	$w_{net.fin}$	$w_{fin}$
16.67mm to 10mm	20mm to 14.3mm	33.3mm to 16.67mm

Instantaneous deformation $u_{inst}$

$u_{inst}$ (instantaneous deformation) of our beam can be calculated with the load of the characteristic loadcombination. Looking at all loadcombinations we can see that LC3 leads to the biggest load where the live load is the leading and the snow load the accompanying variable action.

LC3

$1.08 \frac{kN}{m^2} + 1.0 \frac{kN}{m^2} + 0.7 * 1.0 \frac{kN}{m^2}$

$2.78 \frac{kN}{m^2}$

Transforming this load into a line load gives us:

$2.78 \frac{kN}{m^2} \cdot 0.8m = 2.22 \frac{kN}{m}$

Which we now can put in the deflection formula for line loads on simply supported beams.

$$u_{inst} = \frac{5}{384} \cdot q \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} $$
$$u_{inst} = \frac{5}{384} \cdot 2.22 \frac{kN}{m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 9.22 \cdot 10^7 mm^4} = 17.85mm$$

Finally we can check the utilization.

$$\eta = \frac{u_{inst}}{w_{inst}}$$

$$\eta = \frac{17.85mm}{16.67mm} = 1.07$$

Increase of Cross-section dimensions

Width w = 100 mm
Height h = 240 mm
Moment of inertia $I_{y} = 1.15 * 10^8 mm^4 $

Now we run the deflection calculation again with the updated dimensions.

$$ \frac{5}{384} * 2.22 \frac{kN}{m}  * \frac{(5m)^4}{11 \frac{kN}{mm^2} * 1.15 * 10^8 mm^4} = 14.28mm$$

and the utilization.

$$\eta = \frac{14.28mm}{16.67mm} = 0.85$$

Final deformation $u_{fin}$

$u_{fin}$ (final deformation) of our beam can be calculated by adding the creep deformation $u_{creep}$ to the instantaneous deflection $u_{inst}$. Therefore we will look at how we calculate the creep deflection of LC3.

The creep deformation due to dead load is calculated as

$$u_{creep.g} = u_{inst.g} \cdot k_{def} $$
$$u_{creep.g} = \frac{5}{384} \cdot g_{k} \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} \cdot k_{def}$$

Where

$k_{def} $ is given in EN 1995-1-1 for solid timber in Service class 1 as 0.6.

$$u_{creep.g} = \frac{5}{384} \cdot 0.86 \frac{kN/m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4 } \cdot 0.6$$
$$u_{creep.g} = 3.33 mm$$

The creep deformation due to the leading variable action (live load in our case – LC3) is calculated as

$$u_{creep.q} = u_{inst.q} \cdot k_{def} \cdot \Psi_{2.q} $$
$$u_{creep.q} = \frac{5}{384} \cdot q_{k} \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} \cdot k_{def} \cdot \Psi_{2.q}$$

Where

$\Psi_{2.q} $ is given in EN 1990 Table A1.1 for imposed loads on roofs as 0.

$$u_{creep.q} = \frac{5}{384} \cdot 0.8 \frac{kN/m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4 } \cdot 0.6 \cdot 0$$
$$u_{creep.q} = 0$$

The creep deformation due to the accompanyied variable action (snow load in our case – LC3) is calculated as

$$u_{creep.s} = u_{inst.s} \cdot k_{def} \cdot \Psi_{2.s} $$
$$u_{creep.s} = \frac{5}{384} \cdot q_{k} \cdot \frac{L^4}{E_{0.mean} \cdot I_{y}} \cdot k_{def} \cdot \Psi_{2.s}$$

Where

$\Psi_{2.s} $ is given in EN 1990 Table A1.1 for snow loads in Sweden as 0.2

$$u_{creep.s} = \frac{5}{384} \cdot 0.8 \frac{kN/m} \cdot \frac{(5m)^4}{11 \frac{kN}{mm^2} \cdot 1.15 \cdot 10^8 mm^4 } \cdot 0.6 \cdot 0.2$$
$$u_{creep.s} = 0.43 mm$$

Adding the creep to the instantaneous deflection leads to the final deflection.

$$u_{fin} = u_{inst} + u_{creep.g} + u_{creep.q} + u_{creep.s}$$

$$u_{fin} = 14.28mm + 3.33mm + 0mm + 0.43mm = 18.04mm$$

This leads to a utilization of

$$\eta = \frac{18.04mm}{33.3mm} = 0.54$$