13 Beam Deflection Formulas

ByLaurin Ernst Updated
Beam Deflection formulas for simply supported cantilever and contineous beams point load line load

Calculating reaction forces, internal forces and deflections of beams for different loading scenarios, is one of the things in structural engineering that we do throughout our studies and also careers later on.

While it’s very important to know how to calculate reaction and internal forces, it’s much more difficult to calculate the deflection of beams due to different loads.

In case it’s not a simply supported beam, you most likely have to either look up the formula from a book or use an advanced FEM program.

In this article, we’ll show, the most Important and Easiest Deflection Formulas for Beams due to different loading scenarios like UDL line loads, point loads and external moments.

Now, before we get started, the unit of the deflection is in most cases [mm] for most European countries.

But now, let’s jump into it.

Simply Supported Beam: Uniformly Distributed Line Load

This is the most used static system and deflection formulas🔥.

Line Load | Simply Supported Beam

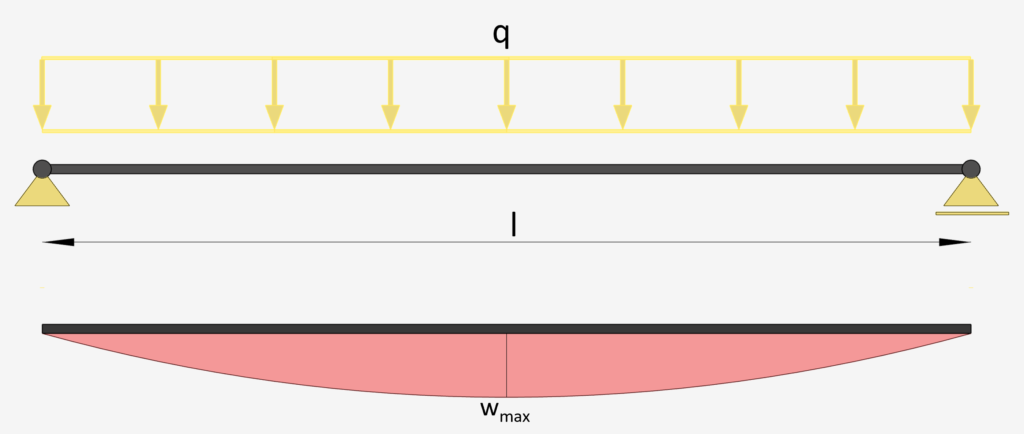
Deflection of Simply supported beam with uniformly distributed line load udl wmax

Max. Deflection $w_{max}$

$w_{max} = \frac{5}{384} \cdot \frac{ql^4}{EI}$

Here are some practical examples of the simply supported beam

Simply Supported Beam: Point Load on Midspan

Point Load Midspan | Simply Supported Beam

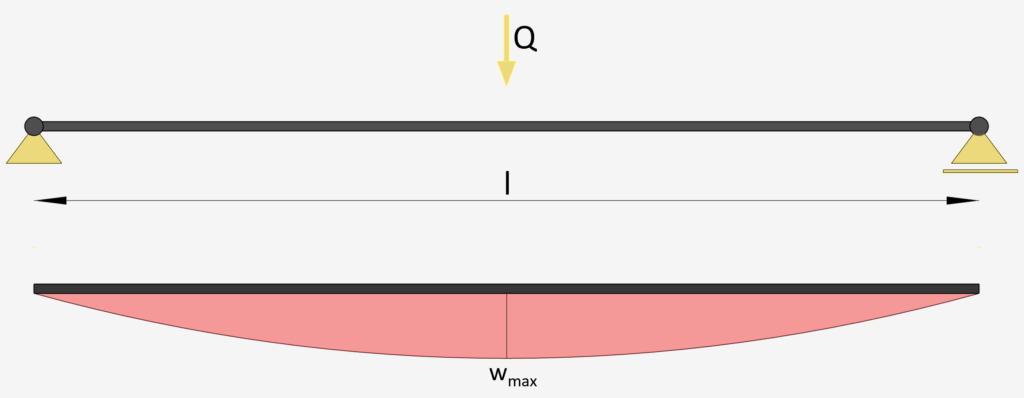
Max. Deflection $w_{max}$

$w_{max} = \frac{Ql^3}{48EI}$

Here is a practical example of the simply supported beam with a Point Load

Simply Supported Beam: Intermediate Point Load

Intermediate Point Load | Simply Supported Beam

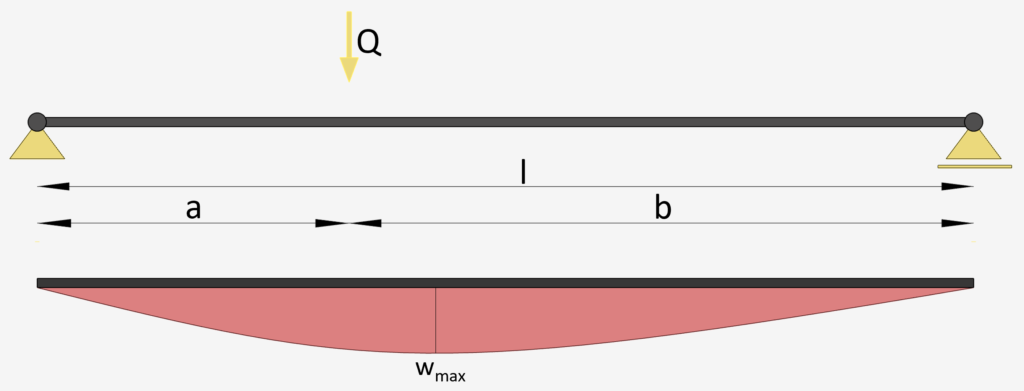
Max. Deflection $w_{max}$

$w_{max} = \frac{Qa\cdot(l^2-a^2)^{3/2}}{9l\cdot \sqrt{3}\cdot EI}$ if a<b

Here is a practical example of the simply supported beam with a Point Load

Simply Supported Beam: Moment on 1 End

1 External Moment | Simply Supported Beam

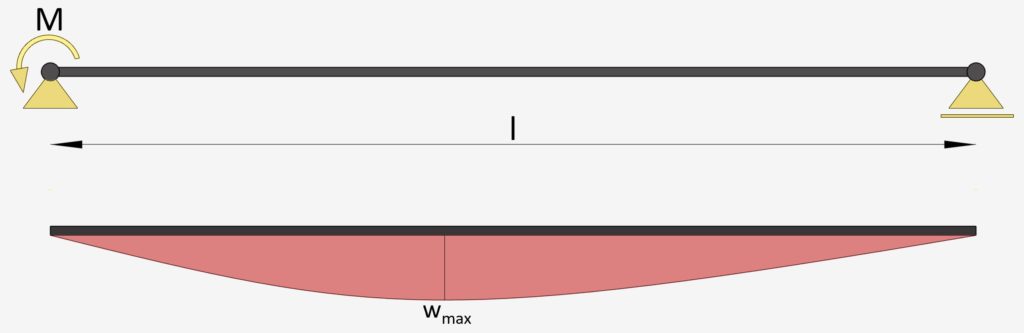
Deflection of Simply supported beam with 1 moment at support wmax.jpg

Max. Deflection $w_{max}$

$w_{max} = \frac{M\cdot l^2}{9\cdot \sqrt{3}\cdot EI}$

Simply Supported Beam: 2 Point Loads

2 Point Loads | Simply Supported Beam

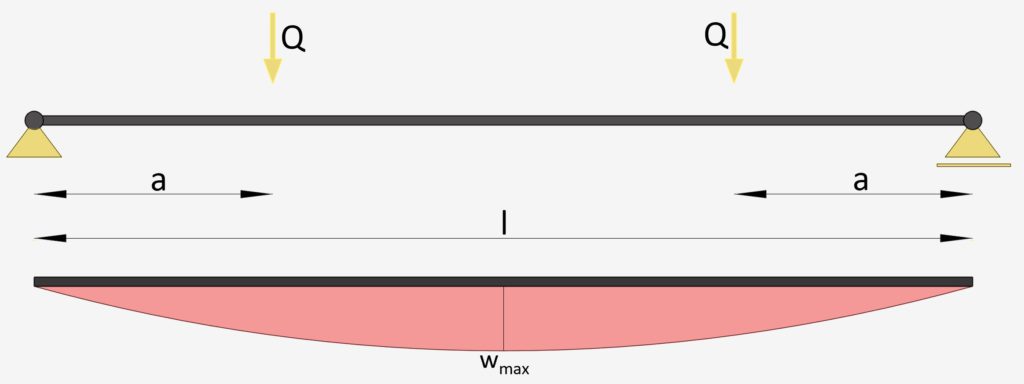
Deflection of Simply supported beam with 2 point loads wmax.jpg

Max. Deflection $w_{max}$

$w_{max} = \frac{F\cdot a}{24\cdot EI} \cdot (3l^2-4a^2)$

Cantilever Beam: Uniformly Distributed Line Load (UDL)

Line Load | Cantilever Beam

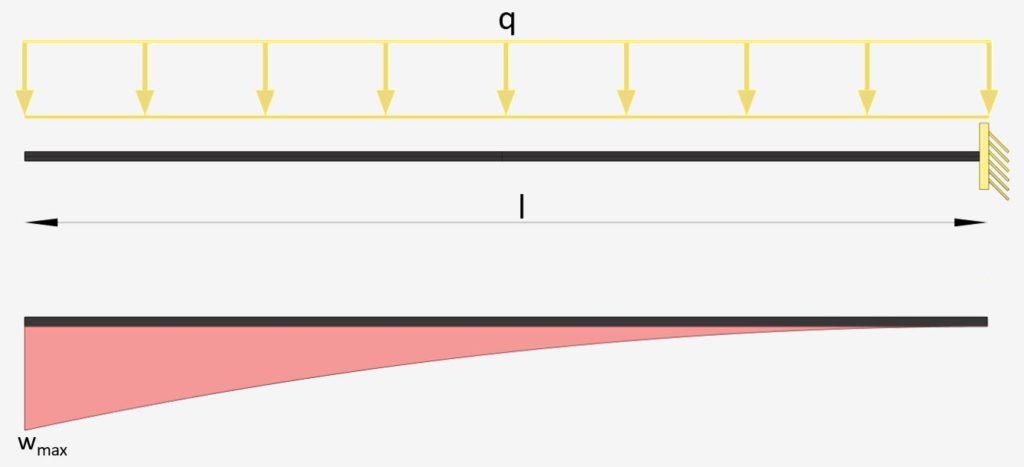
Deflection of Cantilever beam due to uniformly distributed line load udl wmax

Max. Deflection $w_{max}$

$w_{max} = \frac{ql^4}{8\cdot EI}$

Cantilever Beam: Point Load at Free End

Point Load – Free End | Cantilever Beam

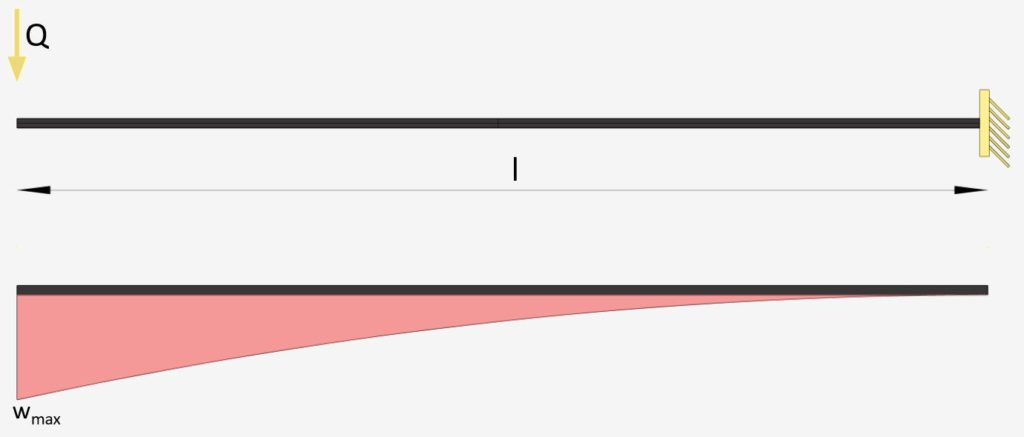
Max. Deflection $w_{max}$

$w_{max} = \frac{Ql^3}{3\cdot EI}$

Cantilever Beam: Intermediate Point Load

Intermediate Point Load | Cantilever Beam

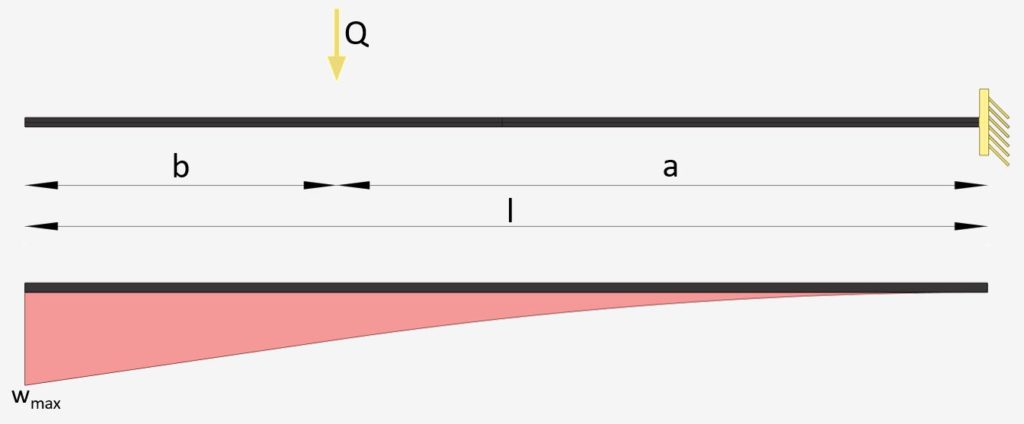
Deflection of Cantilever beam due to intermediate point load wmax

Max. Deflection $w_{max}$

$w_{max} = \frac{Qa^3}{6\cdot EI}\cdot (3l-a)$

2-Span Continuous Beam: Uniformly Distributed Line Load

UDL Line Load | Continuous Beam Deflection

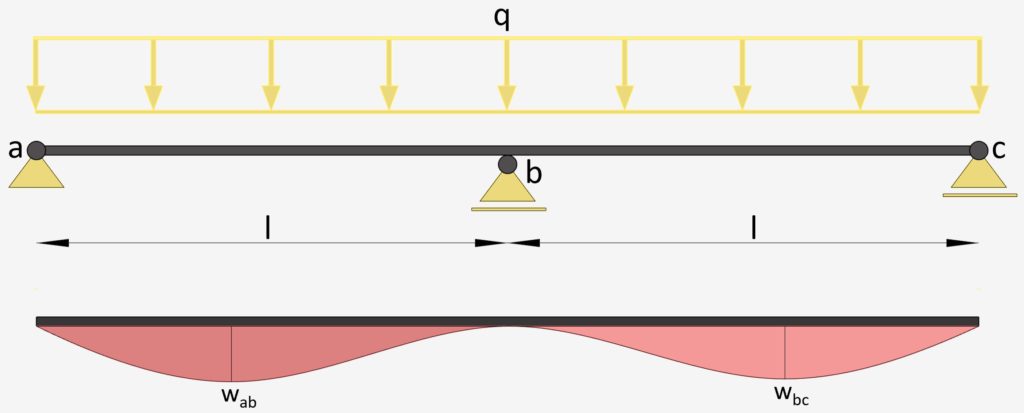
Shows the Deflection of 2 span continuous beam with uniformly distributed line load on both spans wmax

Max. Deflection $w_{max}$

$w_{ab} = 0.00521 \frac{ql^4}{EI}$

$w_{bc} = 0.00521 \frac{ql^4}{EI}$

E = E-modulus of the Beam Material

I = Moment of Inertia of Beam

2-Span Continuous Beam: Uniformly Distributed Line Load on 1 span

UDL Line Load on 1 span | Continuous Beam

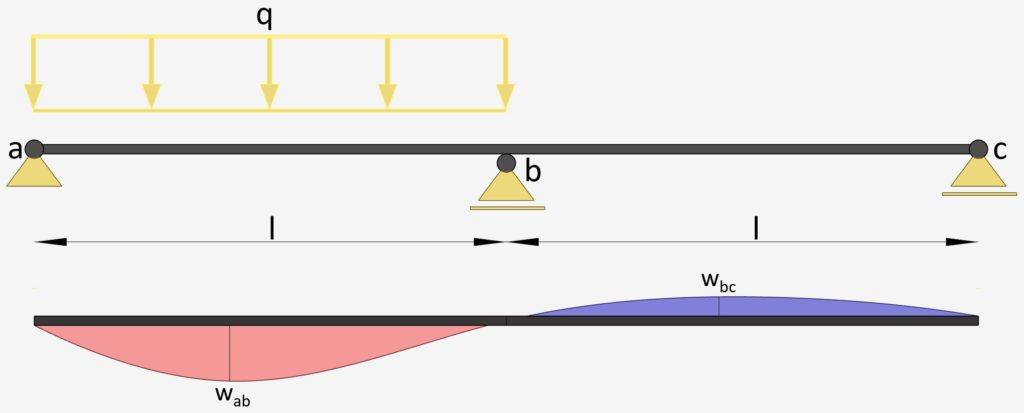
Shows the Deflection of 2 span continuous beam with uniformly distributed line load on 1 spans wmax

Max. Deflection $w_{max}$

$w_{ab} = 0.00911 \frac{ql^4}{EI}$

$w_{bc} = -0.00391 \frac{ql^4}{EI}$

E = E-modulus of the Beam Material

I = Moment of Inertia of Beam

2-Span Continuous Beam: Point Load on 1 span

Point Load on 1 span | Continuous Beam

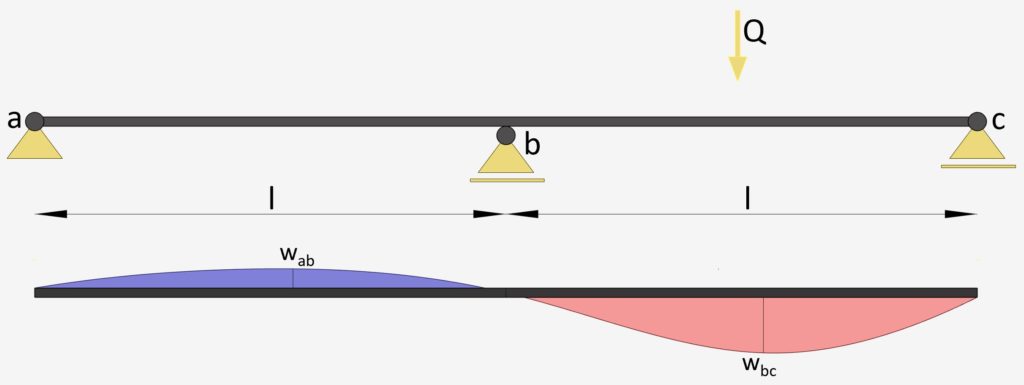
Max. Deflection $w_{max}$

$w_{ab} = -0.00588 \frac{Ql^3}{EI}$

$w_{bc} = 0.01495 \frac{ql^4}{EI}$

E = E-modulus of the Beam Material

I = Moment of Inertia of Beam

3-Span Continuous Beam: Uniformly Distributed Line Load

UDL Line Load | Continuous Beam Deflection

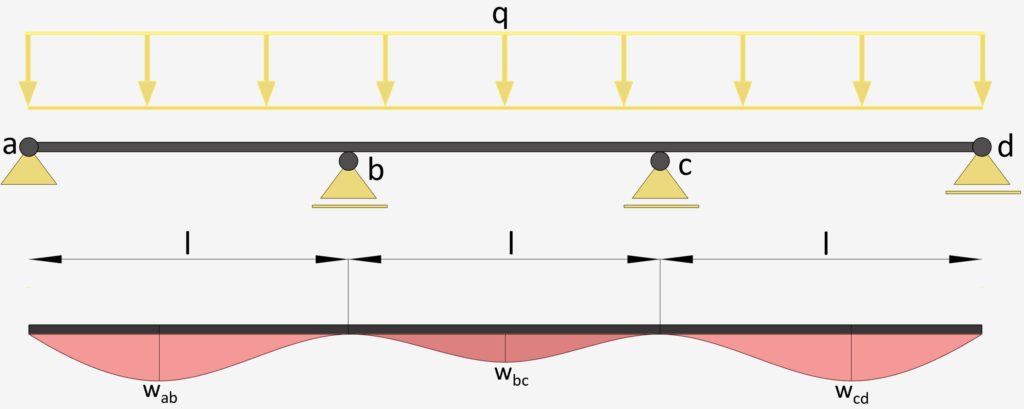
Shows the Deflection of 3 span continuous beam with udl uniformly distributed line load on 3 spans wmax

Max. Deflection $w_{max}$

$w_{ab} = w_{cd} = 0.00677 \frac{ql^4}{EI}$

$w_{bc} = 0.00052 \frac{ql^4}{EI}$

E = E-modulus of the Beam Material

I = Moment of Inertia of Beam

3-Span Continuous Beam: Uniformly Distributed Line Load on Center Span

UDL Line Load on Center | Continuous Beam Deflection

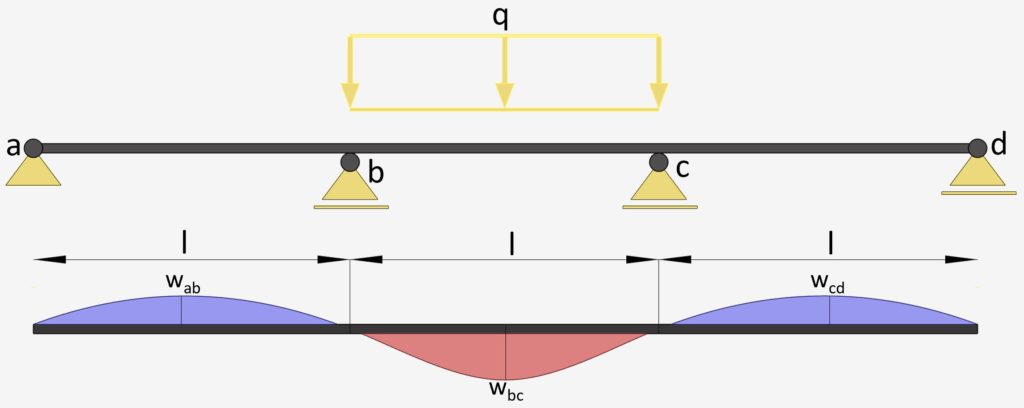
Max. Deflection $w_{max}$

$w_{ab} = w_{cd} = -0.00313 \frac{ql^4}{EI}$

$w_{bc} = 0.00677 \frac{ql^4}{EI}$

E = E-modulus of the Beam Material

I = Moment of Inertia of Beam

If you are new to structural design, then check out our design tutorials where you can learn how to use the deflection of beams to design structural elements such as

Do you miss any deflection formulas for beams that we forgot in this article? Let us know in the comments✍️

Similar Posts