Cross-sectional Area formulas for different shapes and sections

The cross-sectional area is used in many structural calculation methods. The probably most commonly used formula including the cross-sectional area is Navier’s formula, which calculates the stress in any point of a cross-section due to bending and axial forces.
\begin{equation}
\sigma = \frac{N}{A} + \frac{M}{I_y} \cdot z
\label{eq:navier}
\end{equation}
While it’s very important to know how to derive and calculate the Cross-sectional areas, some of them might be harder to remember.
To be honest with you, I have probably looked up the formula for a circular cross-sectional area more than 20 times.
In this post we’ll show, the most important and easiest formulas for Rectangular, I/H, circular, hollow circular section but also formulas for L-, T- and U- Shapes.
All will be shown and explained by images and examples.
Now, before we get started, always remember that the unit of the Cross-sectional area is the power of a length unit [$length^2$].
If you would like to use $mm$ in your calculation, then the unit of the Cross-sectional area is $mm^2$.
But now, let’s get started.
1. What is the cross-sectional area?
The cross-sectional area is a geometric property of structural elements such as beams, columns, slabs, etc. and it is used to calculate the axial stresses in Cross-sections. In general it can be said that the greater the dimensions of a cross-section under a given load, the greater the Cross-sectional area and the smaller the axial stress.
2. Cross-sectional area – Rectangular shape/section (formula)
Cross-sectional Area
$A = h \cdot w$
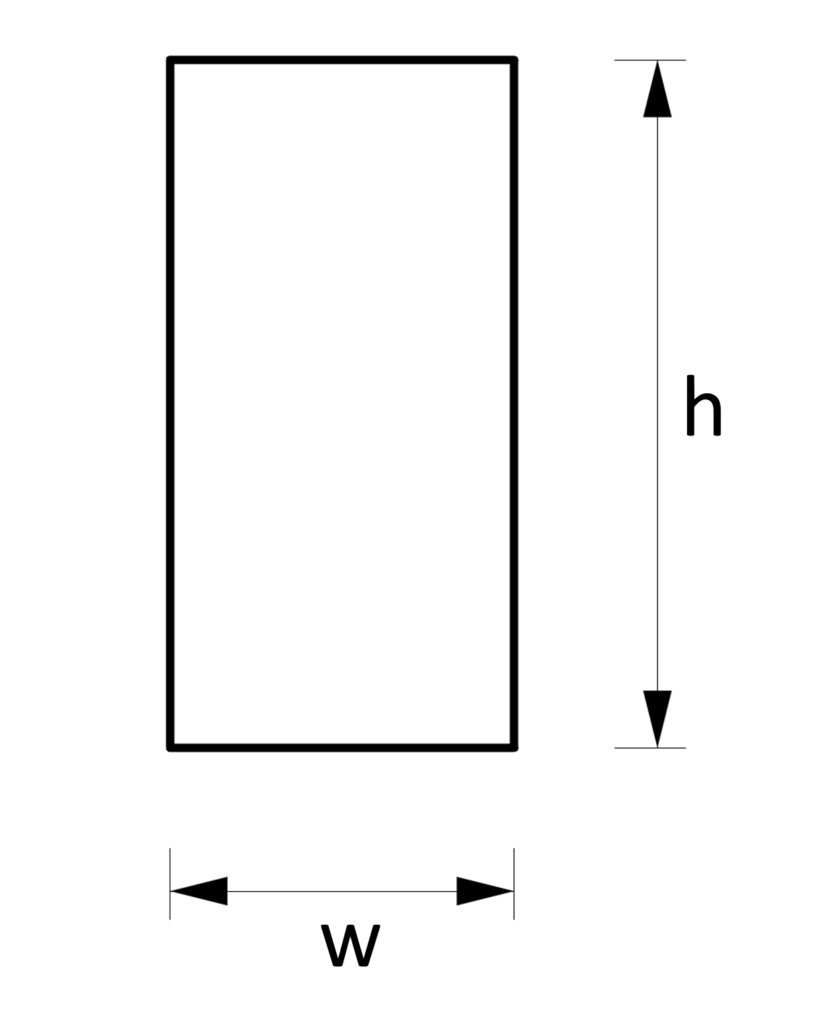
Example calculation
h = 240 mm, w = 120 mm
$A = h \cdot w = 240mm \cdot 120mm = 2.88 \cdot 10^4 mm^2$
Where is the Cross-sectional area of a rectangular Cross-section used in real projects?
- Structural buckling calculation of columns
- Structural compression verification of timber, steel and concrete elements
- Prestressed concrete beams
3. Cross-sectional area – I shape/section (formula)
Cross-sectional Area
$A = 2 \cdot w \cdot t_f + (h-2t_f) \cdot t_w$
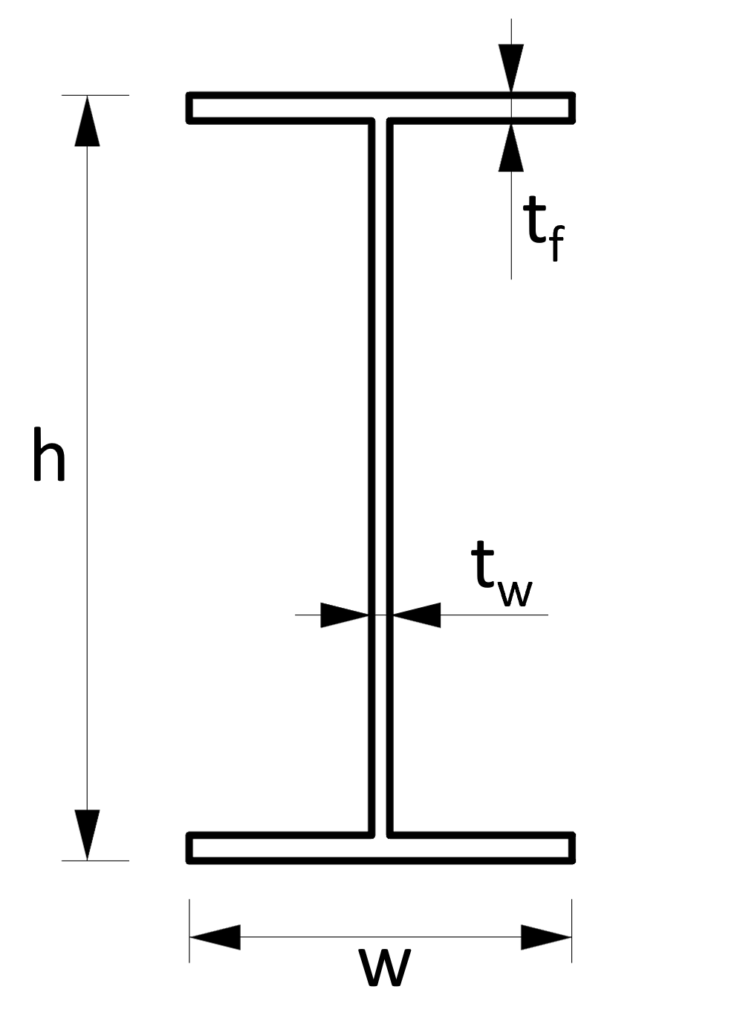
Example calculation
$h$ = 300mm, $w$ = 150mm, $t_f$ = 10mm, $t_w$ = 7mm
$A = 2 \cdot w \cdot t_f + (h-2t_f) \cdot t_w = 2 \cdot w \cdot t_f + (h-2t_f) \cdot t_w = 4960 mm^2$
Where is the Cross-sectional area of I Cross-section used in real projects?
- Structural axial stress calculation of steel columns/beams
- Structural buckling calculation of columns
4. Cross-sectional area – Circle/Circular section (formula)
Cross-sectional Area
$A = \pi \cdot (\frac{D}{2})^2$
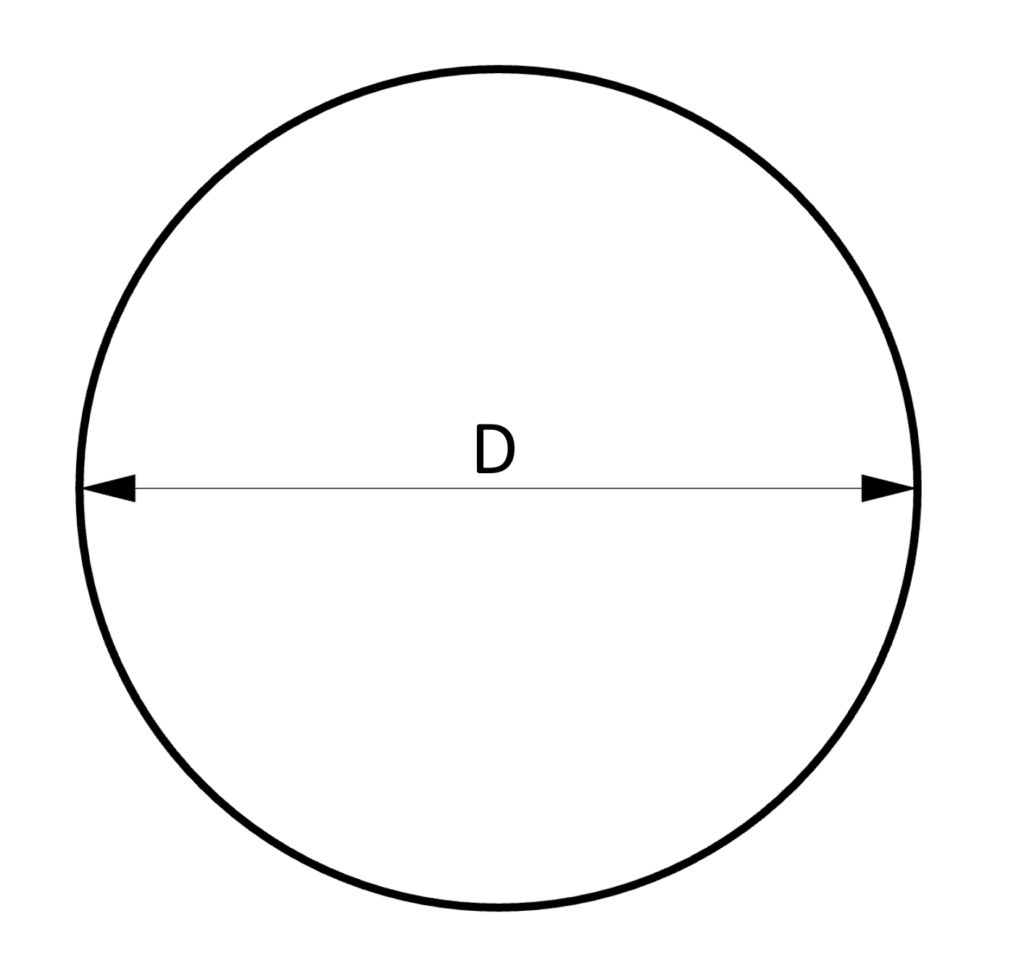
Example calculation
D = 100mm
$A = \pi \cdot (\frac{D}{2})^2 = \pi \cdot (\frac{100mm}{2})^2 = 7853.98 mm^2$
Where is the Cross-sectional area of a circular section used in real projects?
- Structural axial stress calculation of steel wind bracing rods
- Structural axial stress calculation of concrete column
5. Cross-sectional area – Hollow circular tube Section (formula)
Cross-sectional Area
$A = \pi \cdot ((\frac{D}{2})^2 – (\frac{d}{2})^2)$
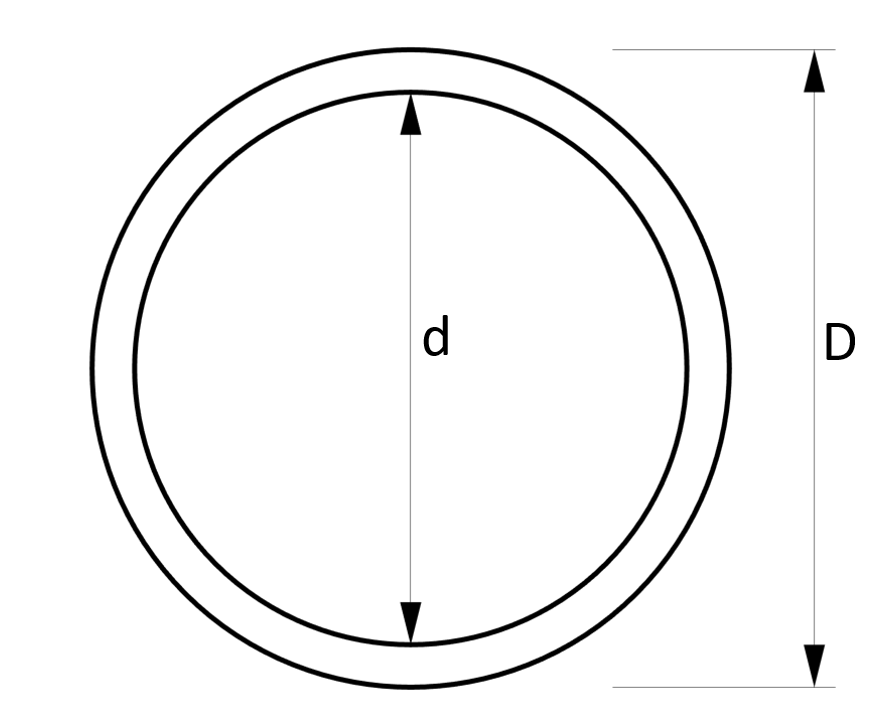
Example calculation
D = 100mm, d = 90mm
$A = \pi \cdot ((\frac{D}{2})^2 – (\frac{d}{2})^2) = \pi \cdot ((\frac{100mm}{2})^2 – (\frac{90mm}{2})^2) = 1492.26 mm^2$
Where is the Cross-sectional area of a circular section used in real projects?
- Structural axial stress calculation of steel wind bracing rods
- Structural axial stress calculation of steel column
6. Cross-sectional area – Hollow rectangular tube Section (formula)
Cross-sectional Area
$A = W \cdot H – w \cdot h$
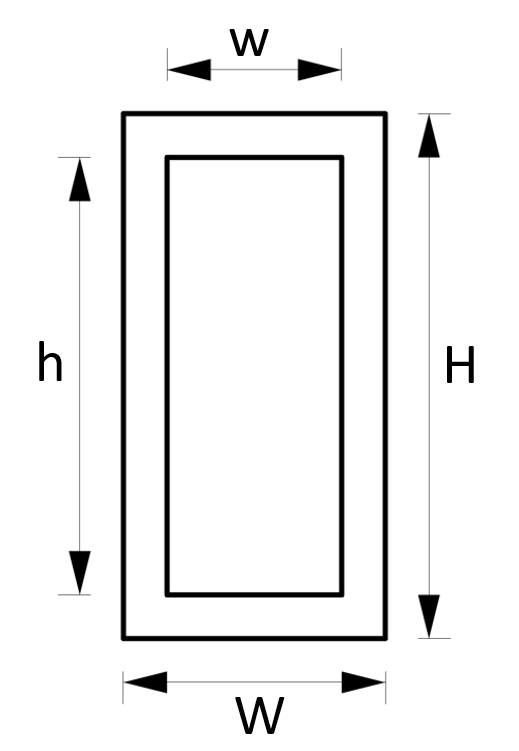
Example calculation
W = 120mm, H = 240mm, w = 100mm, h = 220mm
$A = W \cdot H – w \cdot h = 120mm \cdot 240mm – 100mm \cdot 220mm = 6800 mm^2$
Where is the Cross-sectional area of a hollow rectangular section used in real projects?
- Structural axial stress calculation of a column
7. Cross-sectional area – U profile/C channel (formula)
Cross-sectional Area
$A = 2 \cdot w \cdot t_f + (h-2\cdot t_f) \cdot t_w$
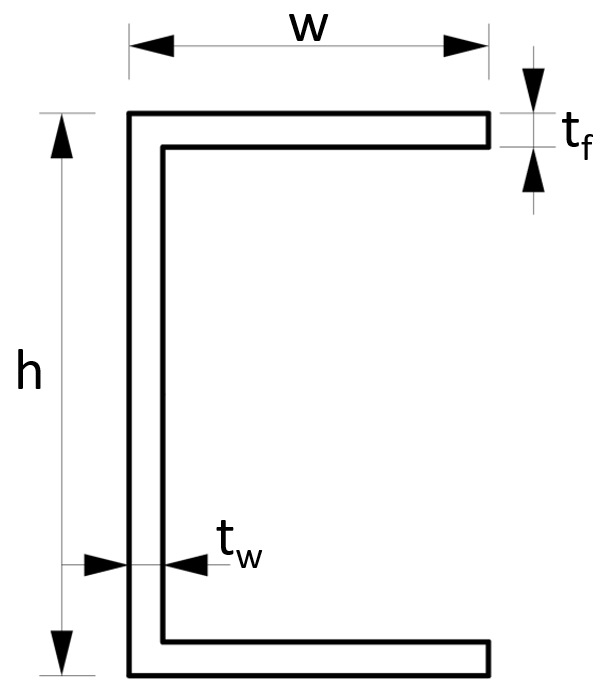
Example calculation
w = 100mm, h = 80mm, $t_f$ = 5mm, $t_w$ = 5mm
Strong axis:
$A = 2 \cdot w \cdot t_f + (h-2\cdot t_f) \cdot t_w = 2 \cdot 100mm \cdot 5mm + (80mm-2\cdot 5mm) \cdot 5mm = 1350 mm^2$
Where is the Cross-sectional area of a U section used in real projects?
- Structural axial stress calculation of a wind bracing steel rods
8. Cross-sectional area – T section/profile (formula)
Cross-sectional Area
$A = w \cdot t_f + h \cdot t_w$
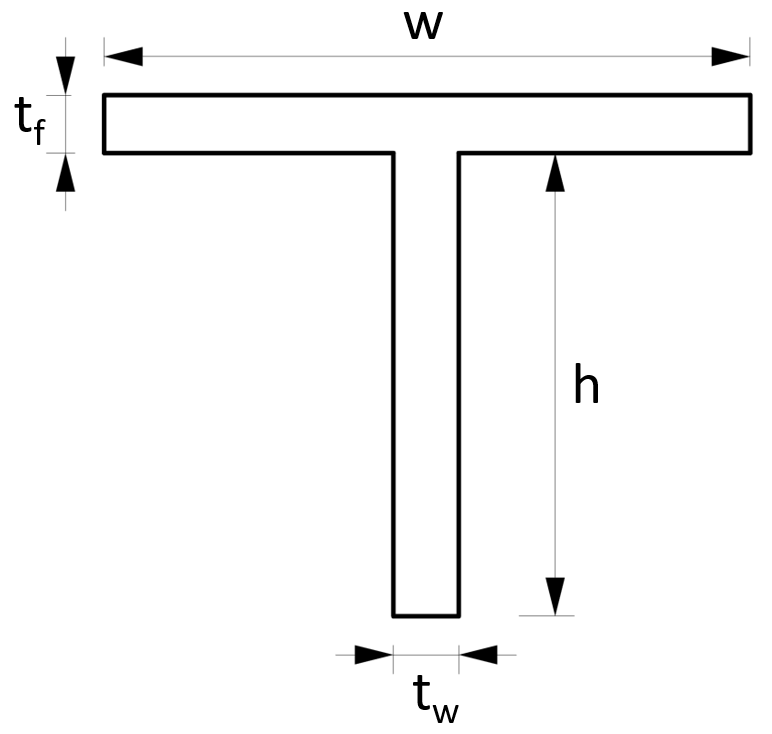
Example calculation
w = 100mm, h = 120mm, $t_f$ = 5mm, $t_w$ = 5mm
$A = w \cdot t_f + h \cdot t_w = 100mm \cdot 5mm + 120mm \cdot 5mm = 1100m^2$
If you are new to structural design, then check out our design tutorials where you can learn how to use the cross-sectional area to design structural elements such as
Do you miss any Cross-sectional area formulas for any shape or Cross-section that we forgot in this article? Let us know in the comments✍️

![How To Find The Centroid [A Step-By-Step Guide]](https://www.structuralbasics.com/wp-content/uploads/2023/04/How-to-find-the-centroid-of-sections-768x439.jpg)


![12 Types of Columns in Buildings [The MOST Used]](https://www.structuralbasics.com/wp-content/uploads/2022/11/Types-of-columns-and-what-a-column-is-1-768x439.jpg)
