7+ Polar Section Modulus Formulas

The polar moment of inertia, quantifies an object/section’s resistance to rotational motion about a specific axis.

This property plays an important role in structural and mechanical engineering, ranging from bolted steel connections to complex machinery analysis.

Every shape has a different polar moment of inertia. In this blog post, we’ll show the formulas for different sections, so you don’t have to calculate them yourself.

Let’s get started. 🚀🚀

What Is The Polar Section Modulus?

The polar section modulus, often denoted as W_p or Z, is a measure of the resistance of a structural shape (cross-section) to torsional/twisting loads.

It is commonly used in engineering and mechanics to analyse and design structures, components and connections subjected to torsional loads, such as shafts, steel tubes and bolted connections.

Formula Of Polar Section Modulus

The formula for the polar section modulus is the following:

$$W_p = \frac{I_p}{r} $$

With,

Ip	Polar moment of inertia
r	Maximum distance from the centroid to the outermost fiber of the shape.

Check out this article to learn how to calculate the polar moment of inertia.

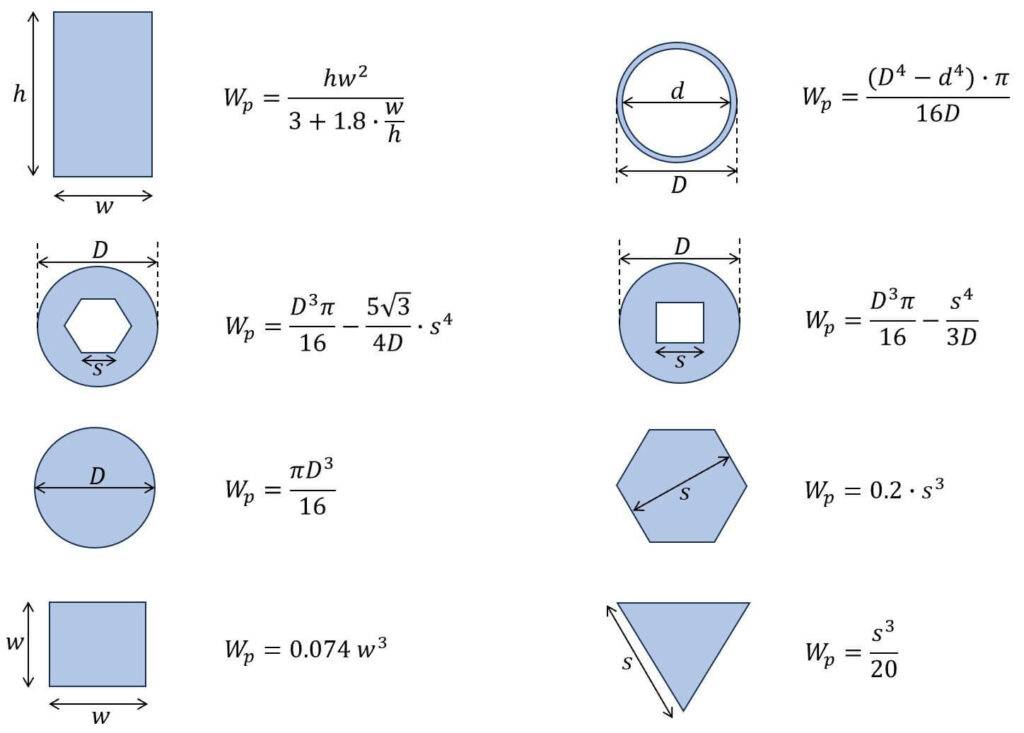
1. Square Section

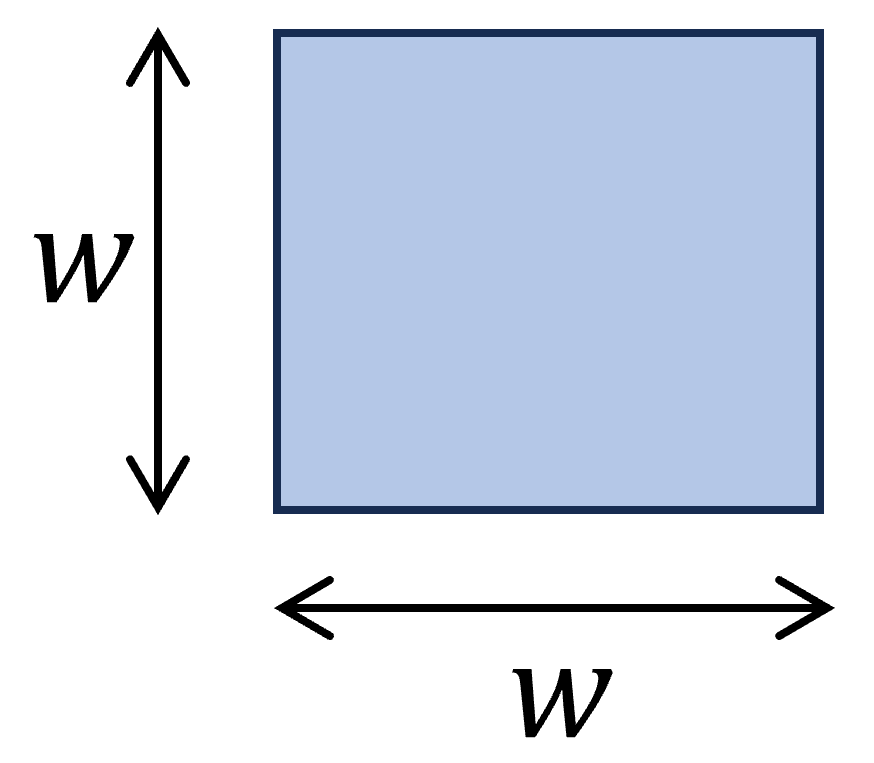
Example calculation

w = 120 mm

$W_p = 0.074 w^3 = 0.074 \cdot (120mm)^3 = 1.28 \cdot 10^5 mm^3$

2. Rectangular Section

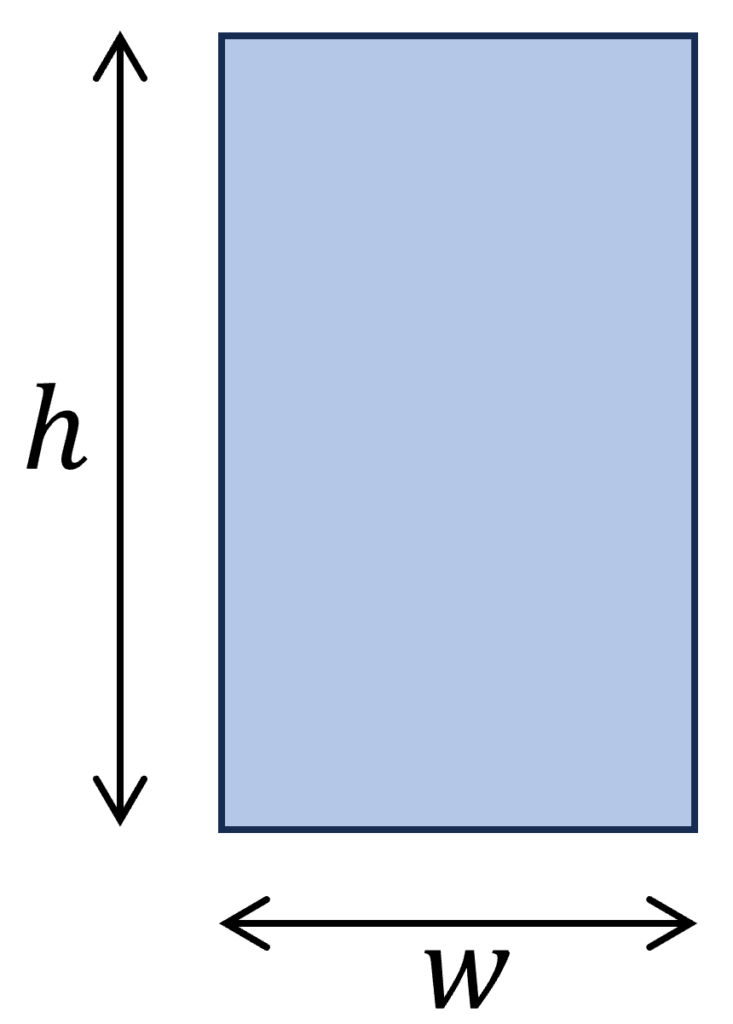
Example calculation

w = 120 mm, h = 240mm

$W_p = \frac{h \cdot w^2}{3 + 1.8 \cdot \frac{w}{h}} = \frac{240mm \cdot (120mm)^2}{3 + 1.8 \cdot \frac{120mm}{240mm}} = 8.86 \cdot 10^5 mm^3$

3. Circle/ Circular Section

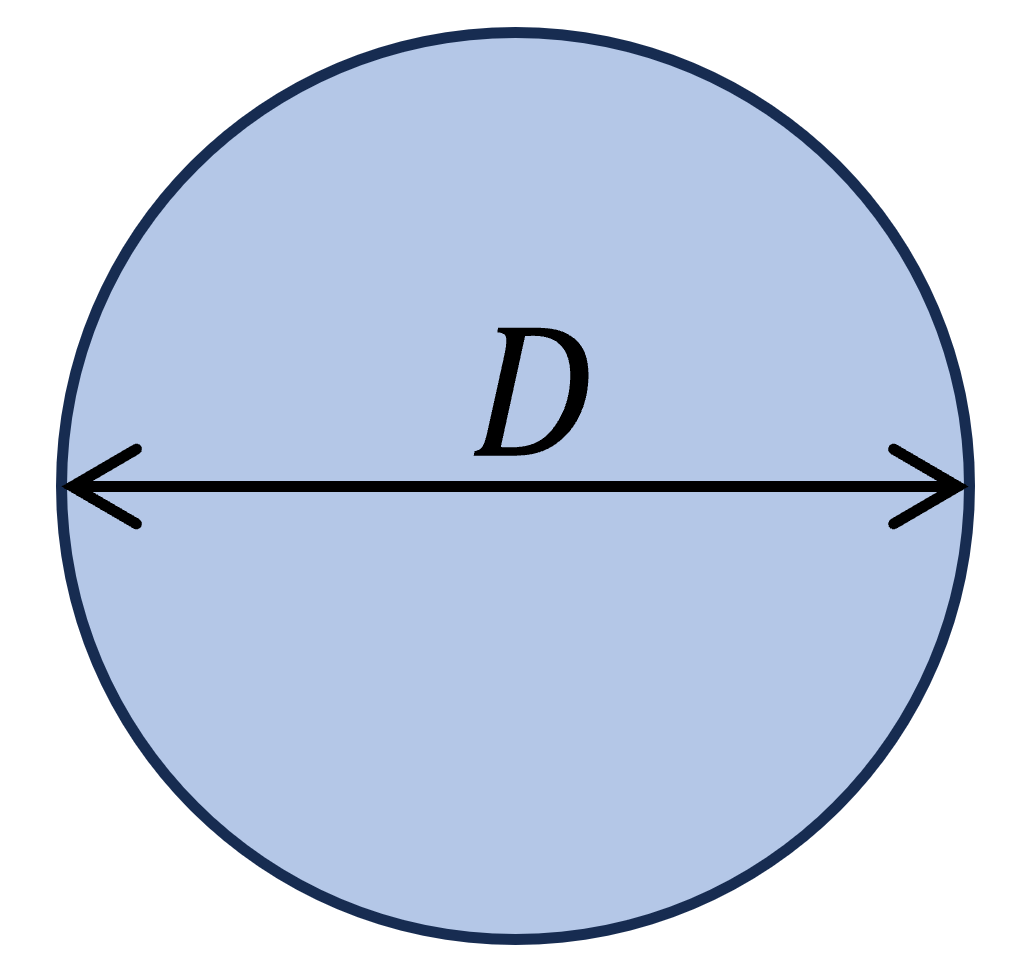
Example calculation

D = 200 mm

$W_p = \frac{\pi \dot D^3}{16} = \frac{\pi \dot (200mm)^3}{16} = 1.57 \cdot 10^6 mm^3$

4. Circular Tube Section

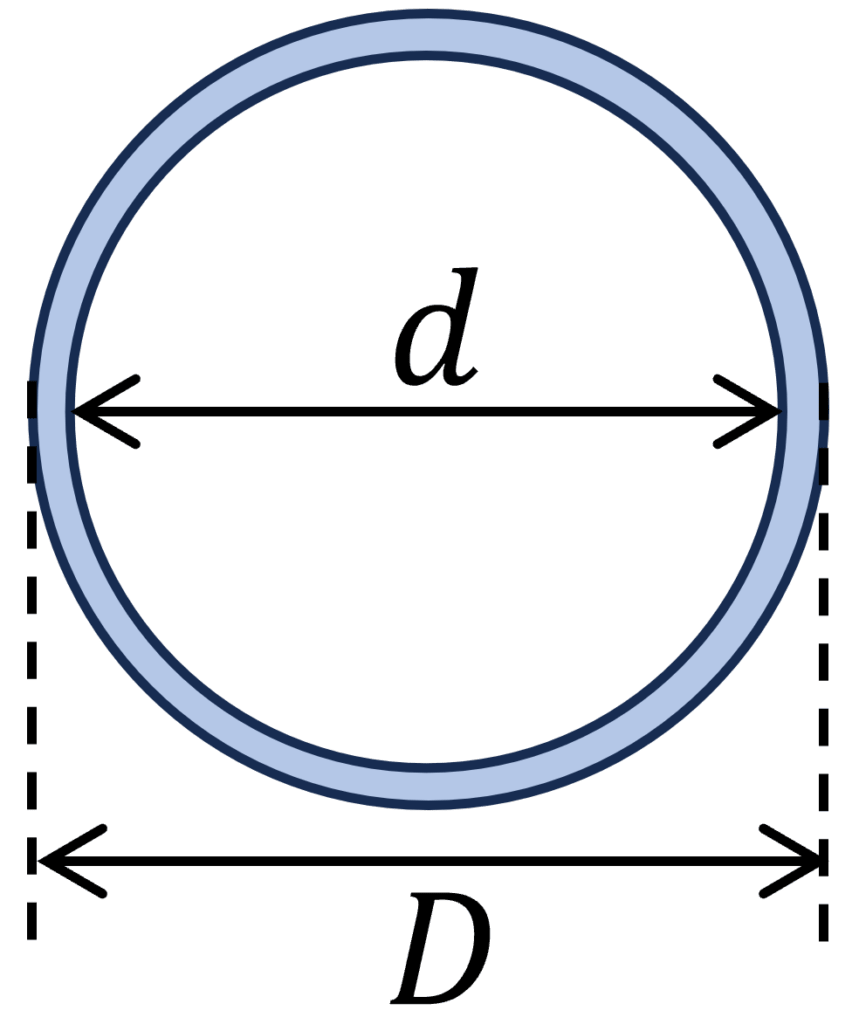
Example calculation

D = 200 mm, d = 180mm

$W_p = \frac{\pi}{16} \cdot (\frac{D^4 – d^4}{D}) = \frac{\pi}{16} \cdot (\frac{(200mm)^4 – (180mm)^4}{200mm}) = 5.4 \cdot 10^5 mm^3$

5. Circular Section With Square Cutout

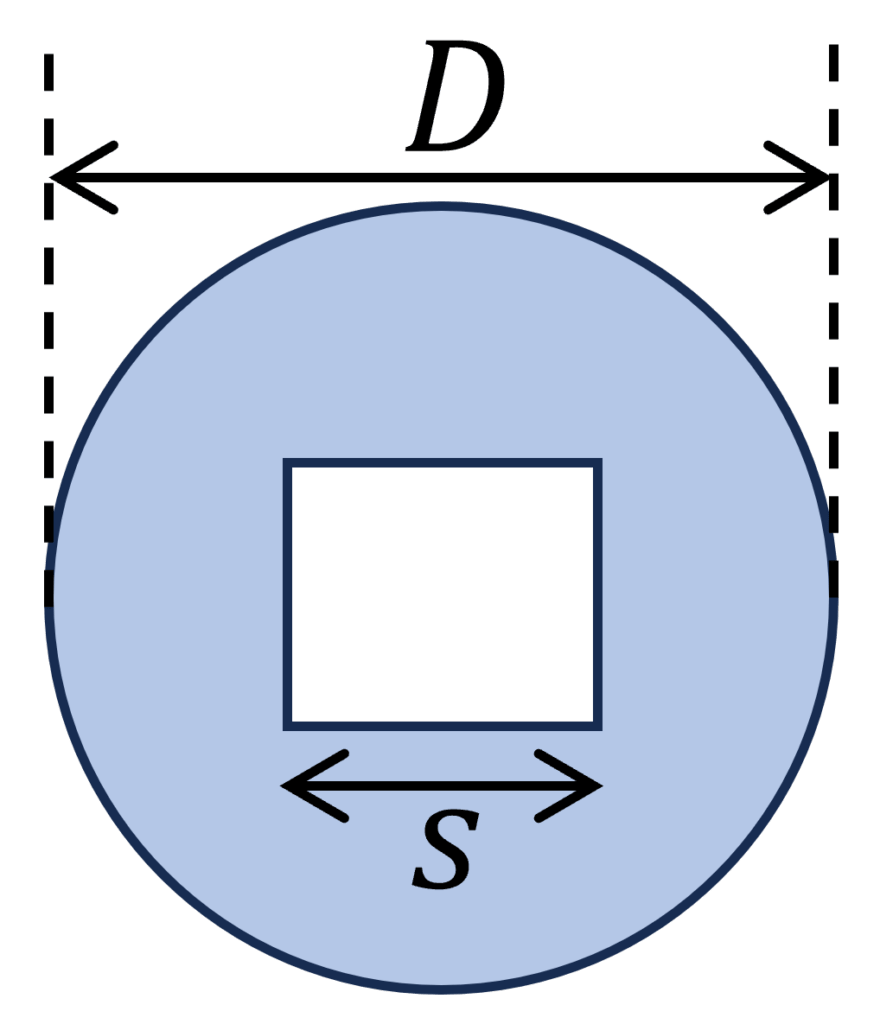
Example calculation

D = 200 mm, s = 100 mm

$W_p = \frac{\pi \cdot D^3}{16} – \frac{s^4}{3D} = \frac{\pi \cdot (200mm)^3}{16} – \frac{(100mm)^4}{3 \cdot 200mm} = 5.2 \cdot 10^6 mm^3$

6. Hexagon Section

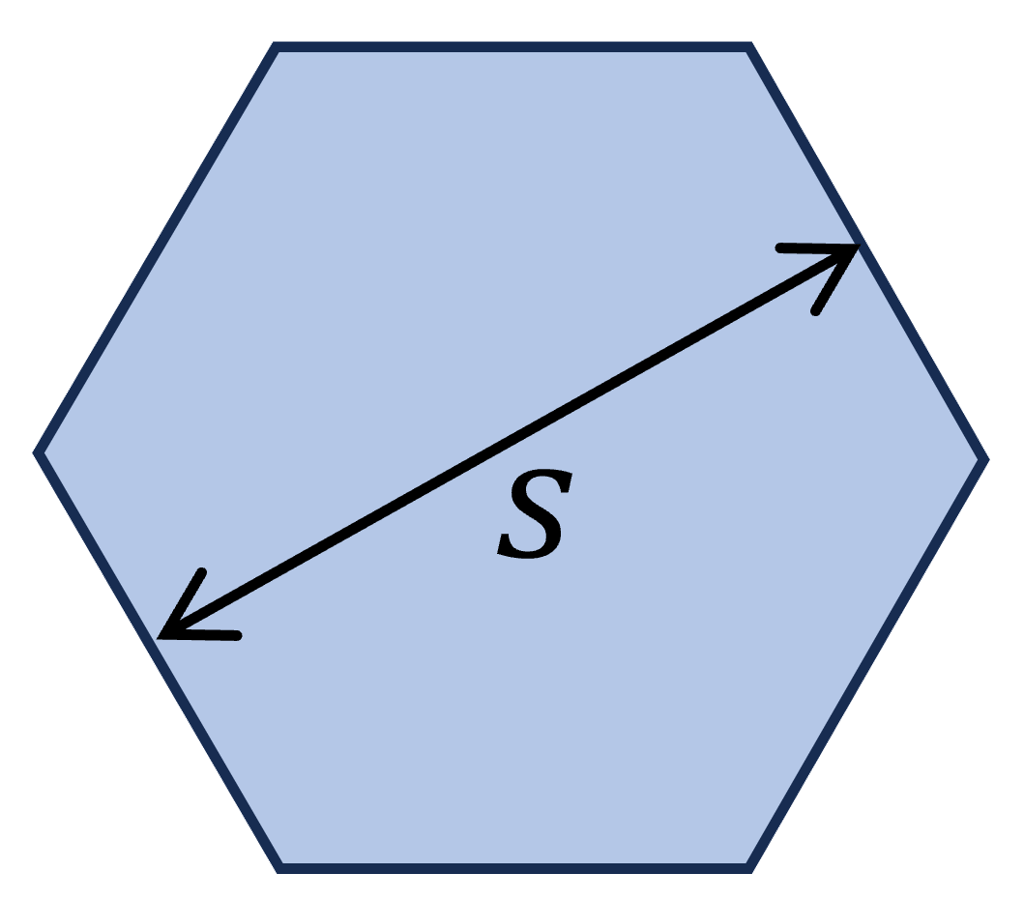
Example calculation

s = 200 mm

$W_p = 0.2 s^3 = 0.2 (200mm)^3 = 1.6 \cdot 10^6 mm^3$

7. Triangular Section

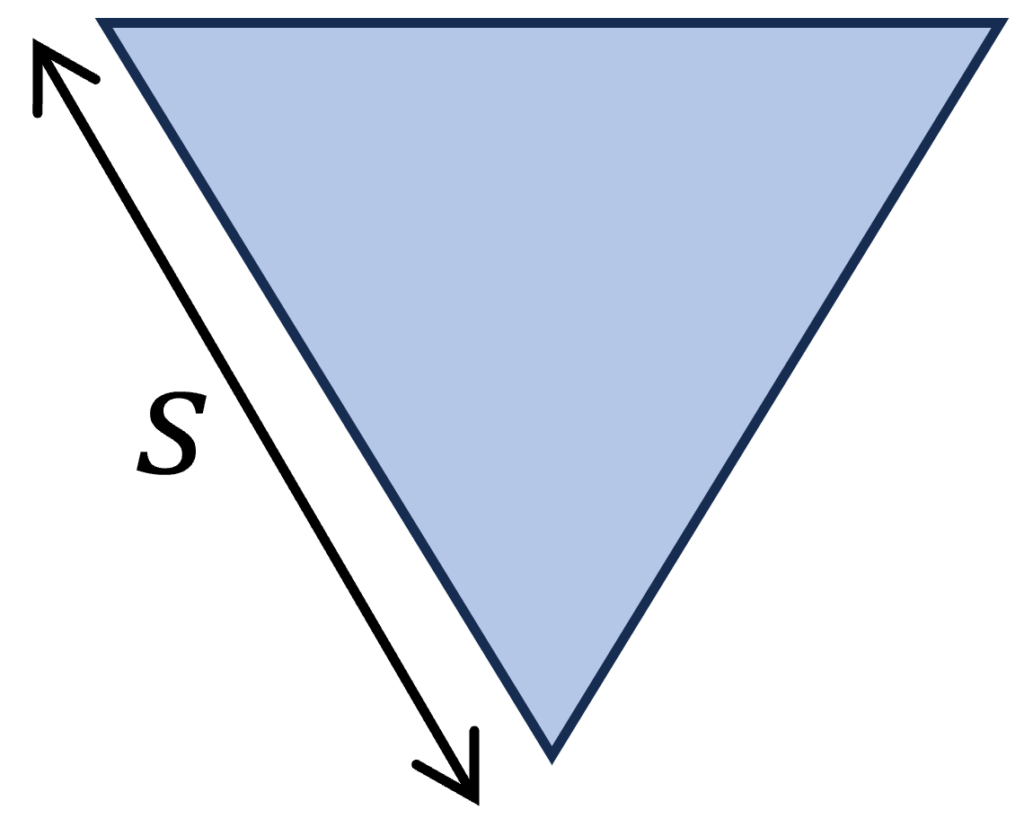
Example calculation

s = 100 mm

$W_p = \frac{s^3}{20} = \frac{s^3}{20} = 5.0 \cdot 10^4 mm^3$

8. Circular Section With Socket Head Cutout

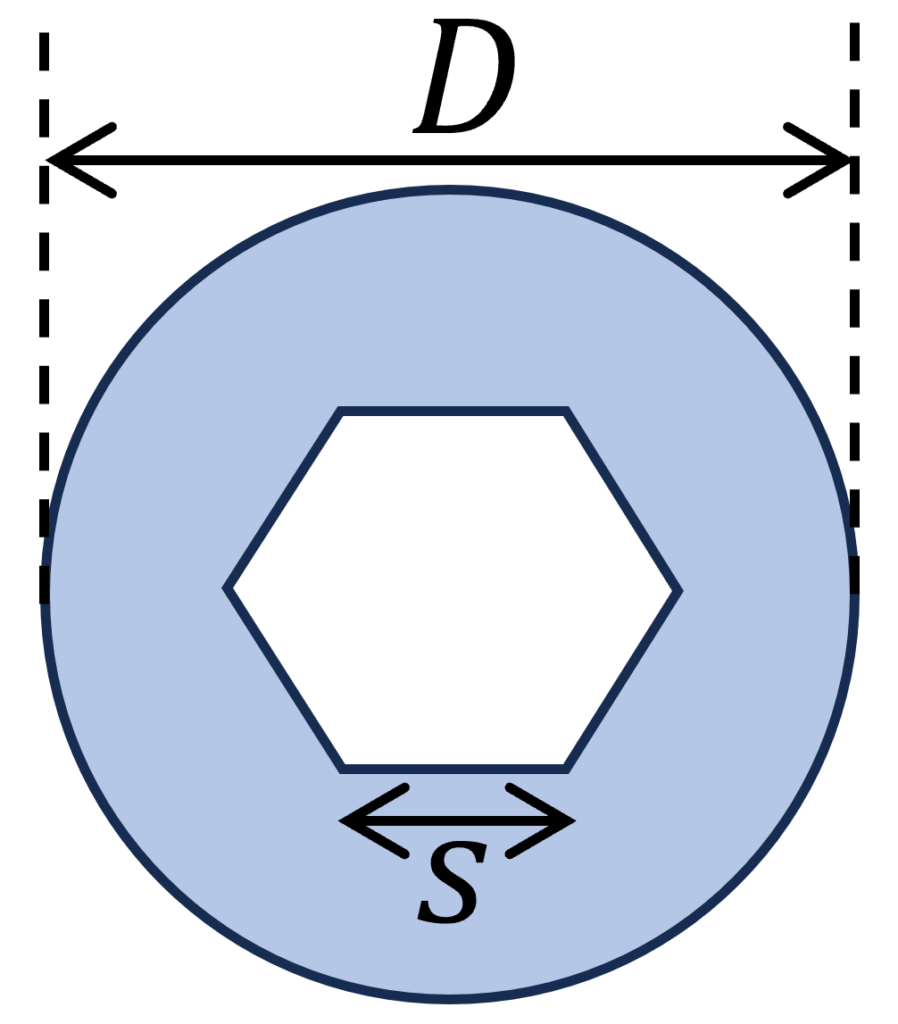
Example calculation

D = 300 mm, s = 100 mm

$W_p = \frac{\pi D^3}{16} – \frac{5 \sqrt{3}}{4D} \cdot s^4$

$W_p = \frac{\pi (300mm)^3}{16} – \frac{5 \sqrt{3}}{4 \cdot 300mm} \cdot (100mm)^4$

$W_p = 4.6 \cdot 10^6 mm^3$

Conclusion

The polar section modulus is an important parameter in structural design of a few elements. Therefore, it’s recommendable to know how to calculate it for different cross-sections.

In the following blog posts, we show step-by-step, how to calculate moments of inertias.

• Moment of inertia of an I-beam
• Moment of inertia calculation

If you are new to structural design, then check out our design tutorials about other structural elements. 👇👇

• Design of timber roof beams
• Buckling design of timber columns
• Buckling design of the collar beam

Do you miss any 2nd polar moment of inertia formula for any shape or cross-section that we forgot in this article? Let us know in the comments. ✍️✍️