How to Calculate The Cross Sectional Area? [A Beginner’s Guide]
Are you struggling with understanding how to calculate the cross-sectional area?
The cross-sectional area is used in many engineering calculations and, therefore, an essential factor in designing components and structures.
In this beginner’s guide, we’ll walk you through the process of calculating the cross-sectional area step-by-step.
We’ll cover different shapes, including circles, rectangles, and more. By the end of this guide, you’ll be able to calculate the cross-sectional area even of complex shapes.
Alright, let’s get started. 🚀🚀
What is The Cross Sectional Area?
The cross-sectional area is the area of the shape created when a 3-dimensional object is cut by a plane. It is used to calculate the amount of material, volume, and strength of an object.
In easy language, it’s the area of a cross-section, and you get this cross-section by cutting through the 3D object.
Let’s look at an example.
In the picture below, a plane cuts through an I beam perpendicular to the length.
Now, if we split the beam into 2 parts at the cutting plane, we get the cross-section of the i beam.
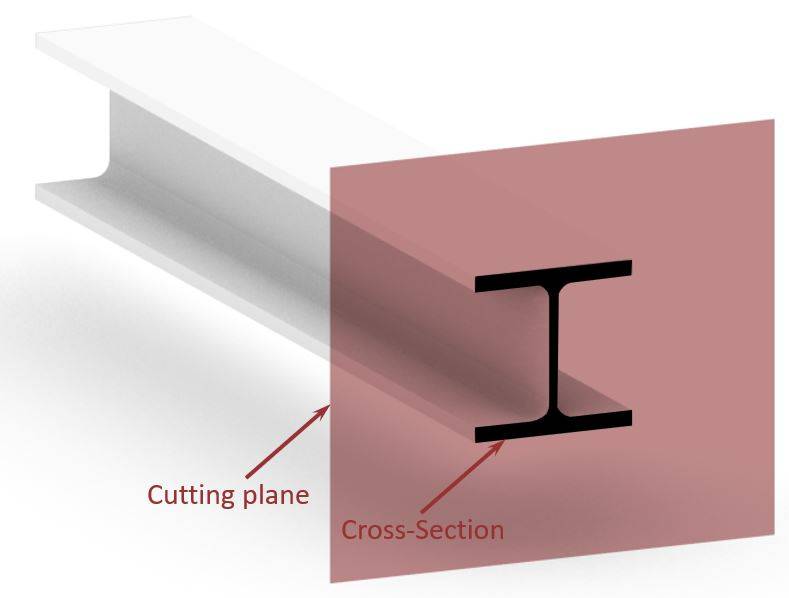
The black area in the picture above is the cross-sectional area of the I beam.
Before we show how to calculate it, it’s important to understand where the cross-sectional area is used. So here are some applications:
Enough talk, let’s get into the calculations.🧮🧮
Calculation of Cross-Sectional Area
As we already learned, the cross-sectional area is a 2D geometry. This means that the normal area formulas apply, utilizing the width, height, etc.
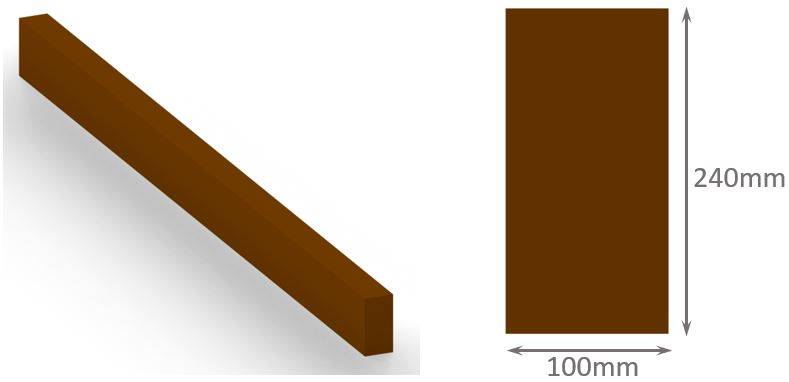
OK, so for example, the cross-section of a timber beam is a rectangle, then the cross-sectional area is calculated as the area of a rectangle:
$$A = w \cdot h$$
With,
w = Width of rectangle
h = Height of rectangle
You can check out this article to see how we used the cross-sectional area of a timber column in the design.
Inserting the values in the equation, the cross-sectional area of the timber beam is calculated as
$$A = 100 mm \cdot 240 mm = 24000 mm^2$$
This was only one example of a cross-section. Let’s have a look at what other sections exist.⬇️⬇️
Types of Cross-Sections
We have already written a Cheat sheet with the cross-sectional area formulas for many different shapes. Make sure to check that out, if you are looking for formulas.
The following cross-sections exist and find use in engineering:
- Rectangular section (Area of a rectangle)
- I or H section (Area of 3 rectangles)
- Circular section (Area of a Circle)
- Hollow circular section (Area of outer circle – Area of inner circle)
- Hollow rectangular section (Area of outer rectangle – Area of inner rectangle)
- C Channel (Area of 3 rectangles)
- T Section (Area of 2 rectangles)
- L Section (Area of 2 rectangles)
Units of Measurement
The unit of the cross-sectional area is mm2 [square milimeter] for most elements. However, if bigger elements such as bridge cross-section are designed, then m2 might be used.
Calculation of Complex Cross-Sectional Areas
In engineering, you sometimes come across complex cross-sections, like in the picture below. In a university course, I had to calculate the cross-sectional area and moment of inertia of that section. It was a beam used on the edge of a cable-stayed bridge deck cross-section.
To be honest with you – who likes to calculate the area of such a profile?
I don’t enjoy that.
Luckily, there is a great tool that can help us to calculate the area.
It’s Rhinoceros and Grasshopper.
1. We simply draw the geometry in Rhinoceros and create a surface from lines.
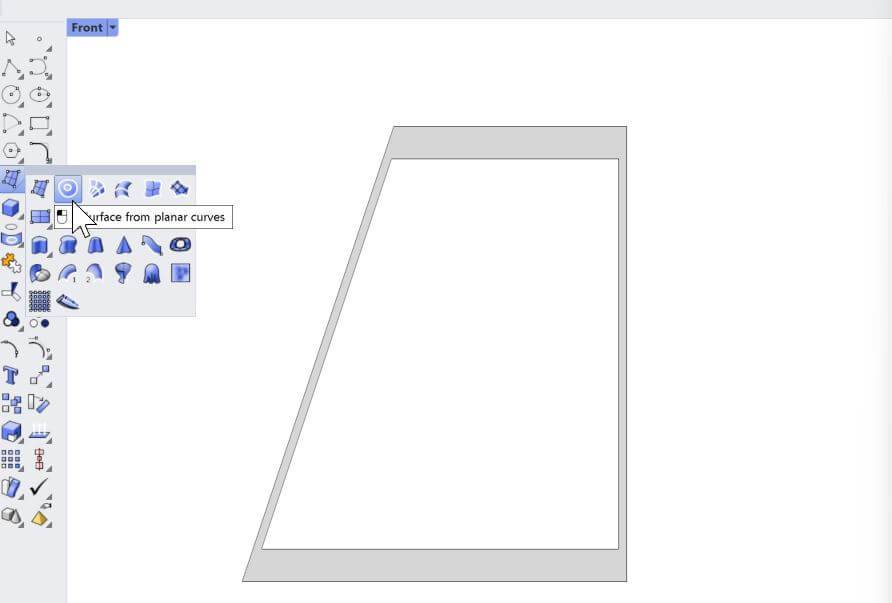
2. We then open Grasshopper.
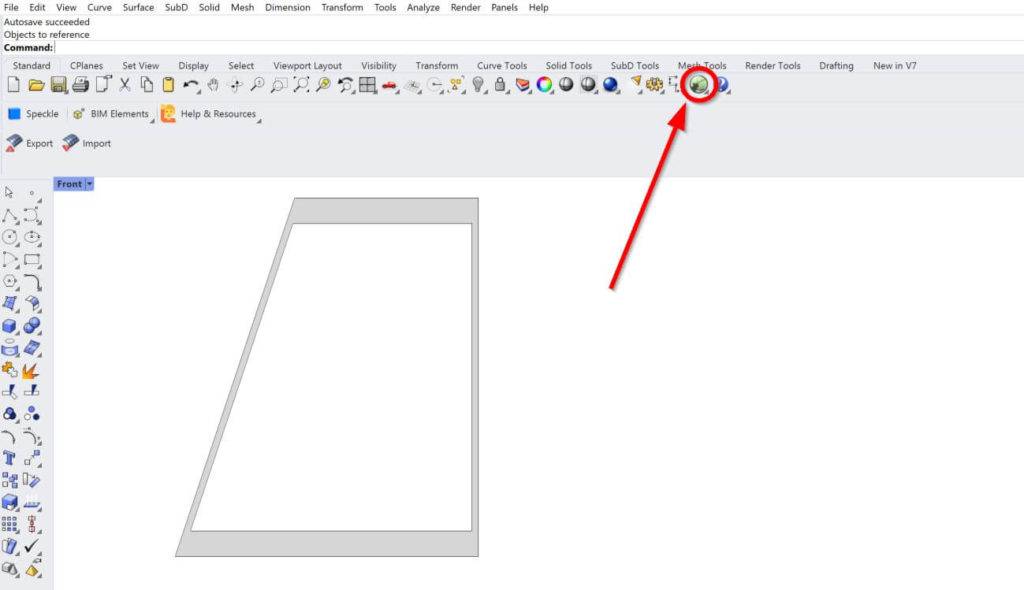
3. In Grasshopper, we click on Surface, Analysis and Area.
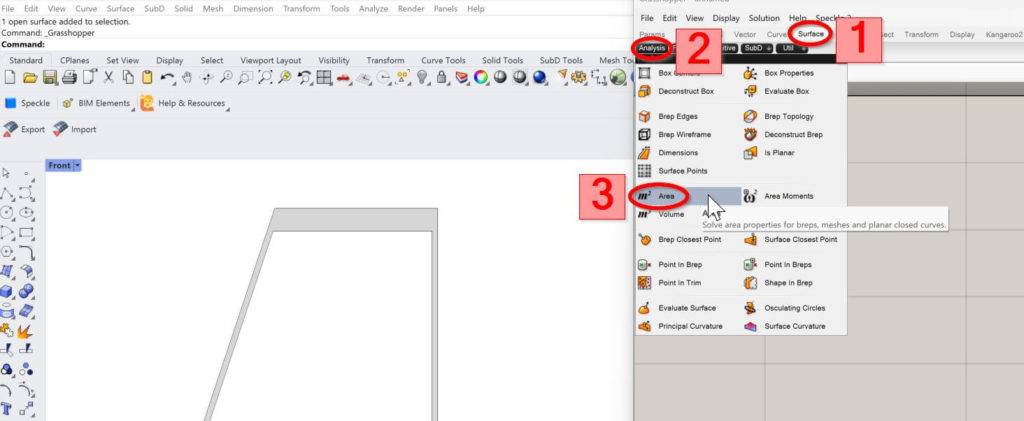
4. Right click on Geometry of the component, click on Set one Geometry and select the surface of the Cross-section.
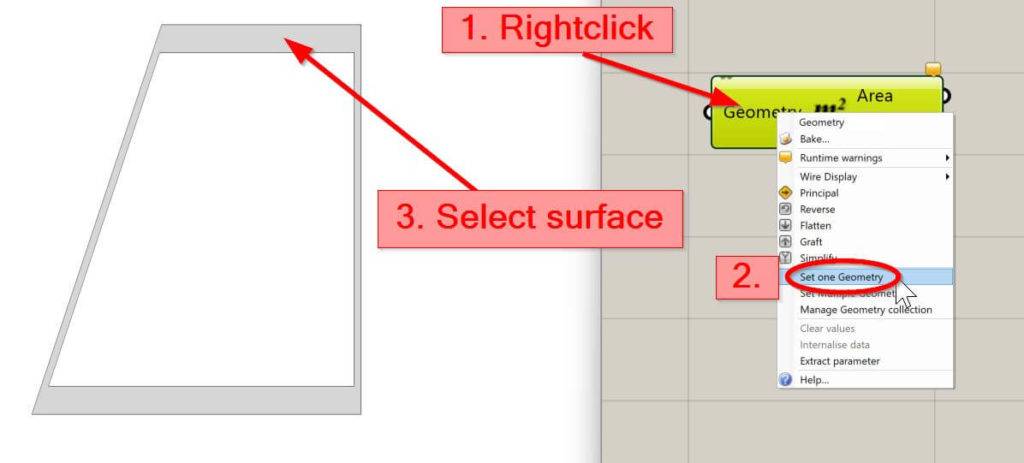
5. Last thing we need to do: Connect a panel with the output of the area component to see the result.
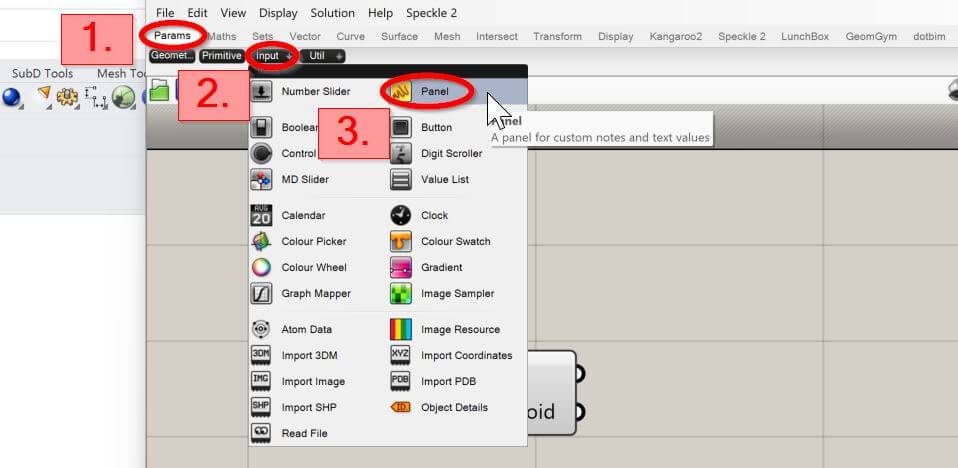
Now, we just connect the area output with the panel input, and we can see the calculated area.
Let us know in the comments below⬇️, if you need a video tutorial for this or if you could follow along.
Conclusion
Now, that you got an understanding of how to calculate the cross-sectional area, you can learn about section modulus and moment of inertia, because these parameters are also cross-sectional properties and used in engineering.
If you want to learn where the cross-sectional area is actually used in structural engineering, then check out the following articles.📖
I hope that this article helped you understand the cross-sectional area and how to go further from here. In case you still have questions.
Let us know in the comments below ✍️.
Cross-Sectional Area FAQ
The cross-sectional area is usually measured in square units, such as square centimeters or square inches. To calculate the cross-sectional area of an object, you would need to cut through the 3D element and then measure the area of the resulting section.
Yes, there are different types of cross-sections depending on the shape of the object. Some common types include circular, rectangular, and H cross-sections.
![How To Find The Centroid [A Step-By-Step Guide]](https://www.structuralbasics.com/wp-content/uploads/2023/04/How-to-find-the-centroid-of-sections-768x439.jpg)