9 Centroid Formulas Of Different Shapes
Are you an engineer, student, or just someone who wants to speed up the calculation of centroid of cross-sections? 🙋♂️🙋♂️
While it’s very important to know how to calculate the centroid of different shapes, it’s much quicker to use formulas. 🚀🚀
In this article, we’ll show, the most important centroid formulas of cross-sections used in structural engineering.
Alright, let’s get started. 🔥🔥
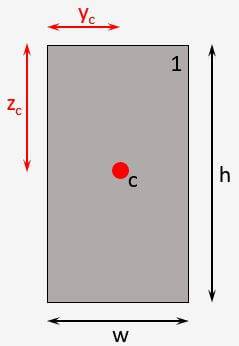
Centroid of Rectangular Section
This is probably the most used cross-section in structural engineering.🔥🔥
Rectangle
Vertical Distance
$z_{c} = \frac{h}{2}$
Horizontal Distance
$y_{c} = \frac{w}{2}$
Here are some practical examples where rectagular cross-sections are used in structural engineering
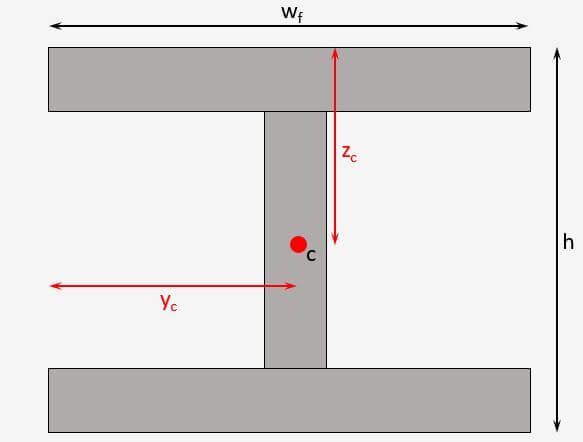
Centroid of Symmetrical I Section
This is the most used cross-section in steel design.🔥🔥
I or H Profile
Vertical Distance
$z_{c} = \frac{h}{2}$
Horizontal Distance
$y_{c} = \frac{w_f}{2}$
Here are some practical examples where I/H cross-sections are used in structural engineering
Centroid of Unsymmetrical I Section
Unsymmetrical I or H Profile
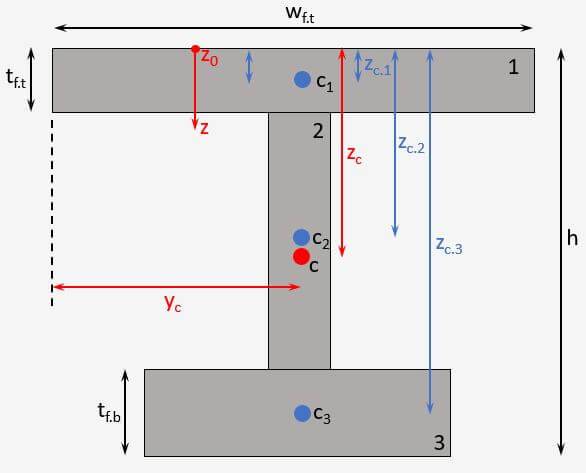
Vertical Distance
$$z_c = \frac{A_1 \cdot z_1 + A_2 \cdot z_2 + A_3 \cdot z_3}{A_1 + A_2 + A_3}$$
Horizontal Distance
$y_{c} = \frac{w_f}{2}$
With,
$A_i$ = Area of the different parts (i = 1, 2, 3)
$c_i$ = Distance from the top edge to the centroids of the different parts (1, 2, 3)
Check out this guide for a full example calculation of the unsymmetrical I section
Centroid of Circular Section
Circle
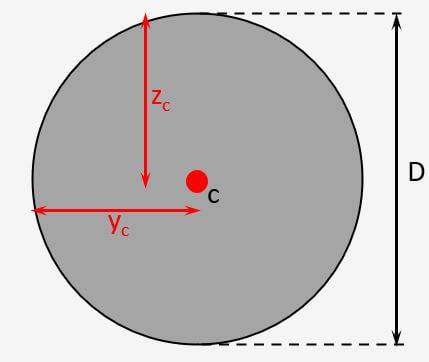
Vertical Distance
$$z_c = \frac{D}{2}$$
Horizontal Distance
$y_{c} = \frac{D}{2}$
Centroid of Hollow Circular Section
Hollow Circle
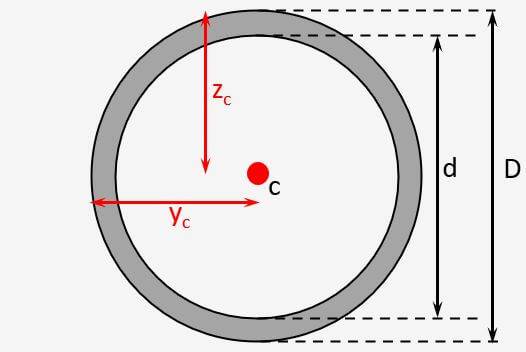
Vertical Distance
$$z_c = \frac{D}{2}$$
Horizontal Distance
$y_{c} = \frac{D}{2}$
Centroid of Unsymmetrical Triangle
Unsymmetrical Triangle
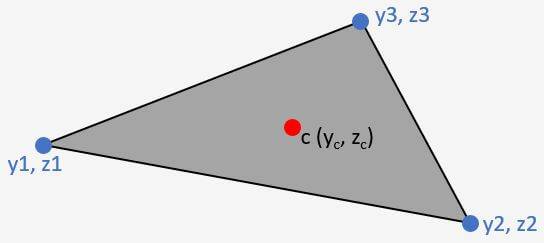
Vertical Coordinate zc
$$z_c = \frac{z_1 + z_2 + z_3}{3}$$
Horizontal Coordinate yc
$y_{c} = \frac{y_1 + y_2 + y_3}{3}$
Centroid of Symmetrical Triangle
Triangle
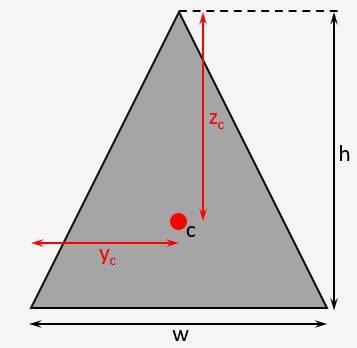
Vertical Distance
$$z_c = \frac{h}{3}$$
Horizontal Distance
$y_{c} = \frac{w}{2}$
Centroid of T Section
T Profile
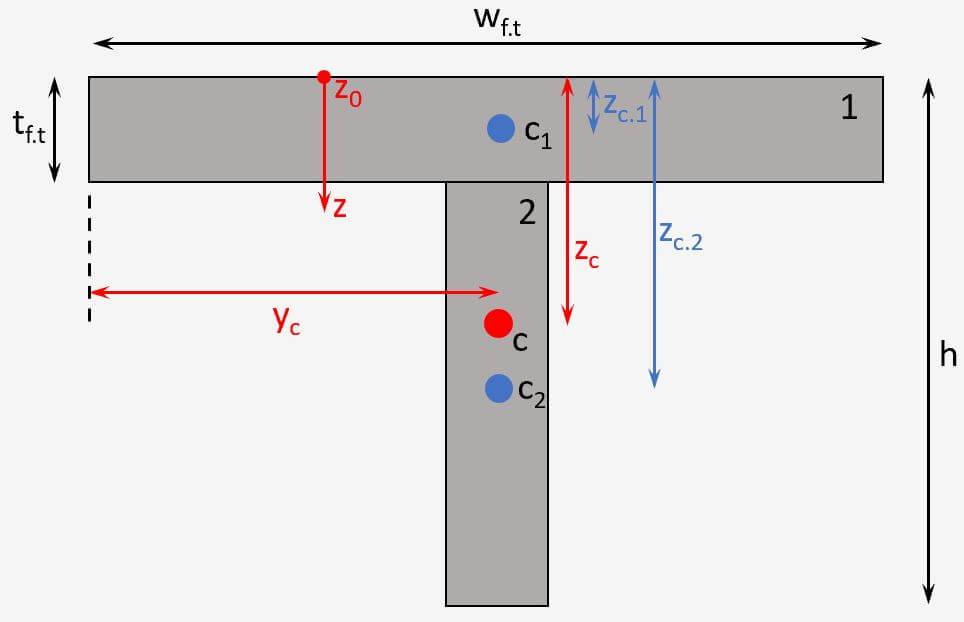
Vertical Distance
$$z_c = \frac{A_1 \cdot z_1 + A_2 \cdot z_2}{A_1 + A_2}$$
Horizontal Distance
$y_{c} = \frac{w_{f.t}}{2}$
With,
$A_i$ = Area of the different parts (i = 1, 2)
$c_i$ = Distance from the top edge to the centroids of the different parts (1, 2)
Centroid of U Section
U Profile
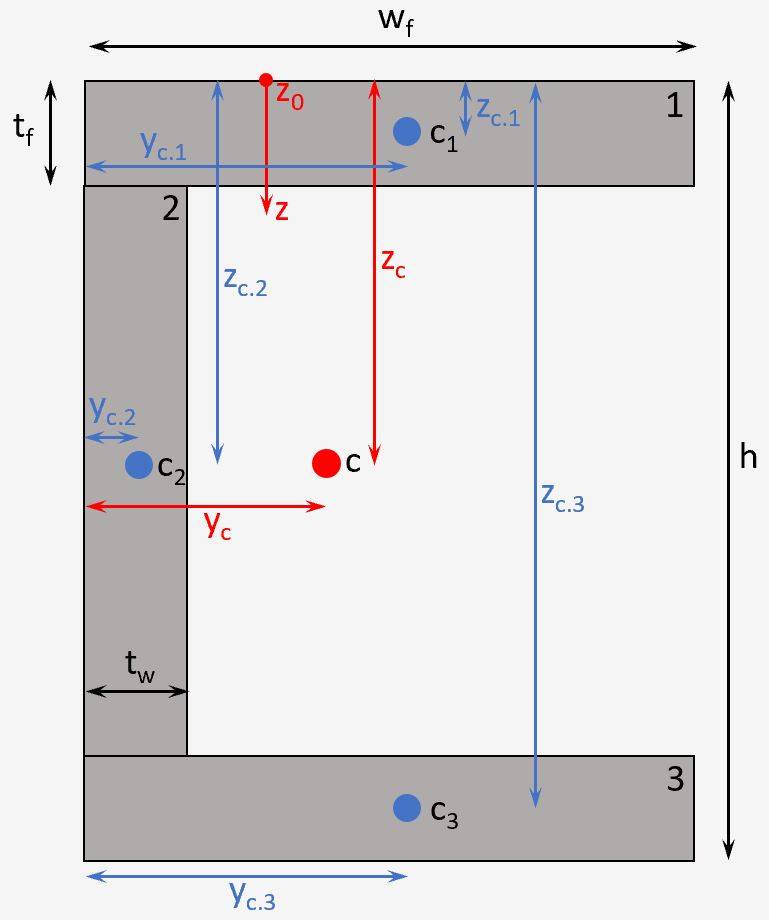
Vertical Distance
$$z_c = \frac{A_1 \cdot z_{c.1} + A_2 \cdot z_{c.2} + A_3 \cdot z_{c.3}}{A_1 + A_2 + A_3}$$
Horizontal Distance
$$y_c = \frac{A_1 \cdot y_{c.1} + A_2 \cdot y_{c.2} + A_3 \cdot y_{c.3}}{A_1 + A_2 + A_3}$$
Conclusion
Calculating the centroid of a cross-section is usually the first step in calculating the moment of inertia or section modulus. Check out those detailed guides. ⬇️⬇️
In case you already know how to calculate moment of inertia and section modulus, here are formula articles to speed up your design calculations.
I hope that this post helps you speed up your engineering calculations.
In case you still have questions.
Let us know in the comments below. ✍️✍️
Centroid Formulas FAQ
Centroid formulas are equations that help you find the coordinates of the centroid of a shape. In other words, the distance from the top, bottom, left and right edges to the centre of mass of a cross-section is calculated.
To use a centroid formula, you need to know the dimensions of the cross-section of the structural element. Then you can insert those values into the formula to find the centroid.
In short: It’s the center of mass or the geometric center of a 2D shape/cross-section.
![Moment of Inertia Calculation [2024]](https://www.structuralbasics.com/wp-content/uploads/2023/01/Moment-of-Inertia-calculation-768x439.jpg)
![How To Find The Centroid [A Step-By-Step Guide]](https://www.structuralbasics.com/wp-content/uploads/2023/04/How-to-find-the-centroid-of-sections-768x439.jpg)
![How to Calculate The Cross Sectional Area? [A Beginner’s Guide]](https://www.structuralbasics.com/wp-content/uploads/2023/01/how-to-calculate-the-cross-sectional-area-768x439.jpg)
