Section Modulus Calculation [Step-By-Step Guide]

Are you an engineer, student, or someone who is looking to understand better how the section modulus is calculated? 🙋‍♂️🙋‍♂️

The section modulus is a crucial parameter in determining the stability and strength of 3D objects such as beams, columns and slabs.

By understanding the section modulus calculation, you are one step closer to designing the most complex engineering elements. 🔥🔥

In this beginner’s guide, we’ll walk you through the process of determining the section modulus step-by-step.

Alright, let’s get started. 🚀🚀

What is The Section Modulus?

The section modulus is a concept in structural design that measures the bending strength of a cross-section. It plays an important role in determining the stability and load-carrying capacity of beams and columns. It depends on cross-sectional dimensions such as height and width.

In easy language, it’s a geometric property used in the design of flexural members.

In general, there are 2 types of section modulus – the elastic and the plastic. When we talk about the section modulus in this post, we mean the elastic section modulus.

Before we look at the calculation of the section modulus, we have to clarify some concepts.

The section modulus is calculated by cross-sectional dimensions (height, width, etc.). The following paragraphs are for everyone who doesn’t know what a cross-section is or how to determine it from 3D objects.

Everyone, who knows about cross-sections, can directly jump into the calculation section.⬇️

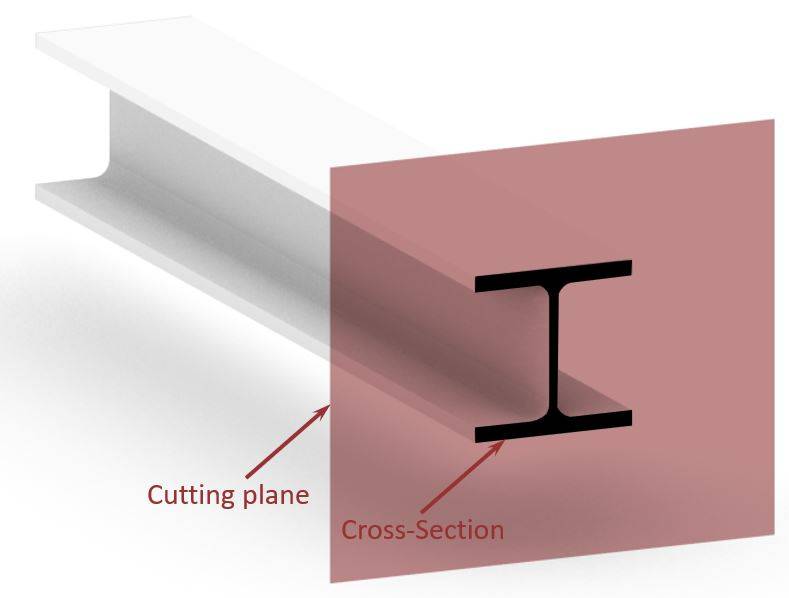
In structural engineering, cross-sections are determined by cutting through a 3D structural object, like a beam, column, slab, etc. perpendicular to its length. This is visualized in the following picture, where the cross-section of an I or H beam is shown.

Before we show how to calculate the section modulus of structural elements, here are some designs where the section modulus is used:

• Bending verification of a steel beam
• Lateral torsional buckling verification of a steel beam

Enough talk, let’s get into the calculations.🧮🧮

Calculation of The Section Modulus

The section modulus is calculated as

Now, let’s clarify that a bit more.

The moment of inertia is a geometric property of a cross-section as much as the section modulus, and you can learn more about it in this post.

A fibre of a cross-section is basically any point in a cross-section. For example, the marked point in the picture below.

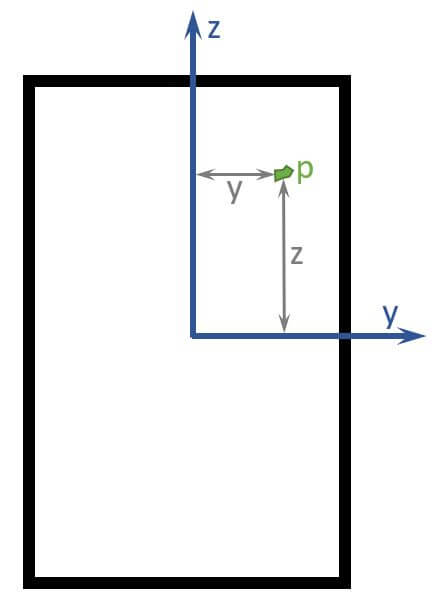
However, in structural design, the fibre with the highest stress is mostly the one farthest away from the neutral axis (y and z) and therefore the section modulus is calculated for that fibre.

For the y-axis of a rectangular cross-section, that would be the bottom or top edge fibres.

And it’s the left and right most outer fibres of a rectangular cross-section for the z-axis.

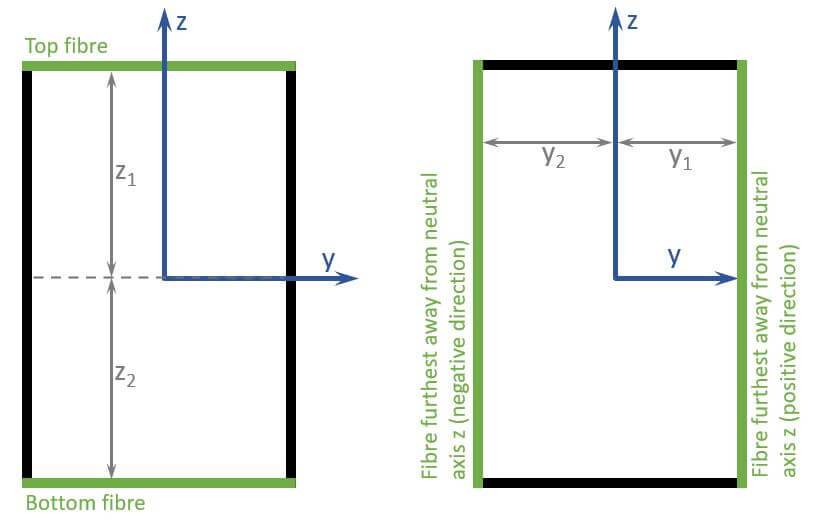
OK! So now let’s calculate the section modulus of a rectangular cross-section. AND as we just saw, we’ll calculate the section modulus of the fibres furthest away from the neutral axis y.🧮🧮

So here are the geometrical properties of the cross-section.

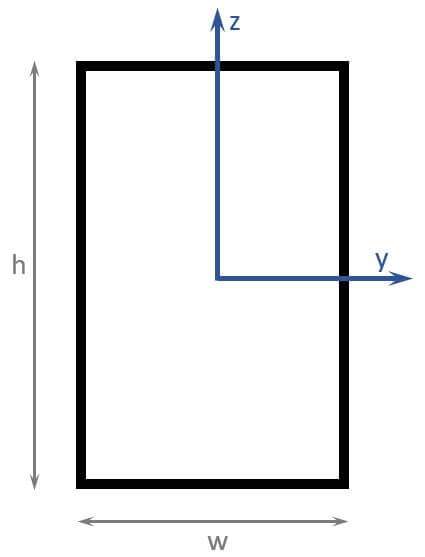
To calculate the section modulus, we need the moment of inertia I_y and the distance from the neutral axis c_z.

We calculated the moment of inertia extensively in this article as

$$I_y = \frac{h^3 \cdot w}{12}$$

So check it out if you wanna see the detailed calculation.

The max. distance from the neutral axis y is in our case half of the cross-section height:

$$c_z = h/2$$

Now, let’s insert those 2 expressions into the formula. ⬇️⬇️

$$W_y = \frac{\frac{h^3 \cdot w}{12}}{\frac{h}{2}}$$

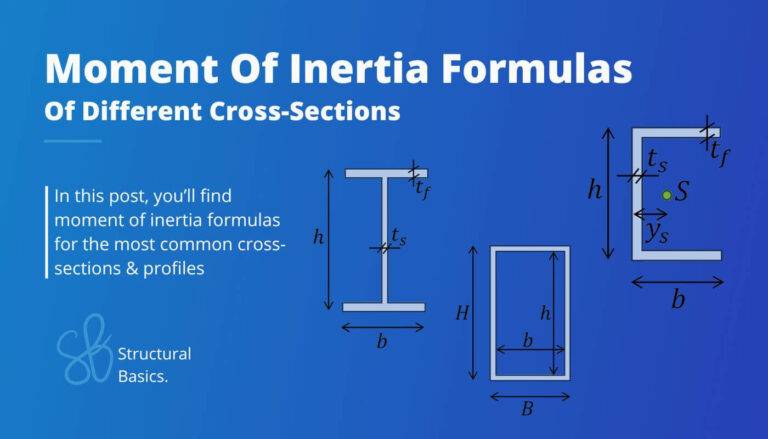
Voilà, this is the section modulus formula for the strong axis of a rectangular cross-section. You can find the formulas of other cross-sections here. ⬅️⬅️

We could do the same now for the weak axis $W_z$ as well.

But let’s safe some space here and use some real dimensions. I guess you have understood the concept. If not, let us know in the comments and we’ll add it. 👍👍

w = 100 mm

h = 240 mm

This results in a section modulus of the strong axis of: ⬇️⬇️

$$W_y = \frac{(240mm)^2 \cdot 100mm}{6} = 9.6 \cdot 10^5 mm^3$$

However, this was only one example of the section modulus of 1 cross-section. Let’s have a look at what other sections exist.⬇️⬇️

Section Modulus for Different Cross-Sections

We have already written a Cheat sheet with the Section Modulus Formulas for many different cross-sections around the strong and weak axis. Make sure to check that out, if you are looking for formulas.

The following cross-sections exist and find use in engineering:

• Rectangular section
• I or H section
• Circular section
• Hollow circular section
• Hollow rectangular section
• C Channel
• T Section
• L Section
• Composite Cross-section (concrete and steel, or concrete and timber)

Units of Measurement

The unit of the section modulus is mm³ [cubic milimeter] for most elements. However, if bigger elements such as bridge cross-section are designed, then m³ might be used.

Calculation of Section Modulus of Complex Cross-Sections

In engineering, you sometimes come across complex cross-sections, like in the picture below. In a university course, I had to calculate the section modulus of that section. It was a beam used on the edge of a deck cross-section of a cable-stayed bridge.

To be honest with you – who likes to calculate the section modulus of such a profile?

It’s time-consuming and prone to errors.❌❌

Luckily, there is a great tool that can help us to calculate the area.

It’s Rhinoceros/Grasshopper.

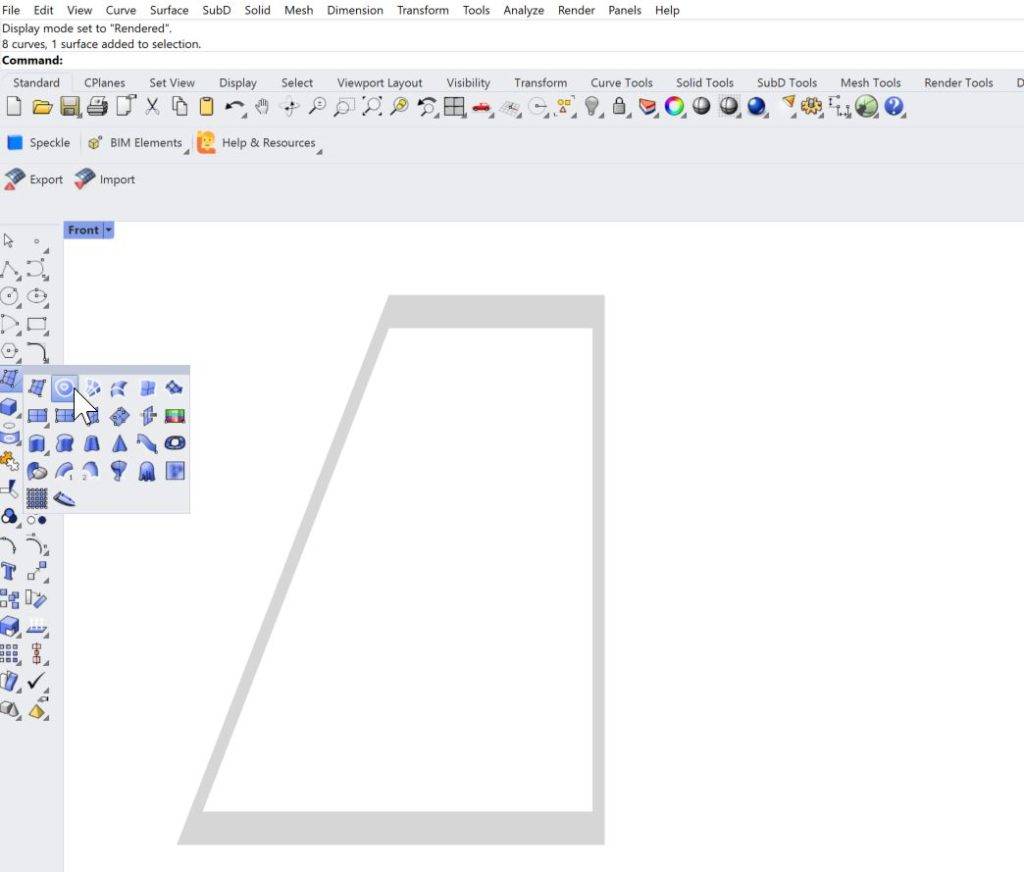
1. We simply draw the geometry in Rhinoceros and create a surface from lines.

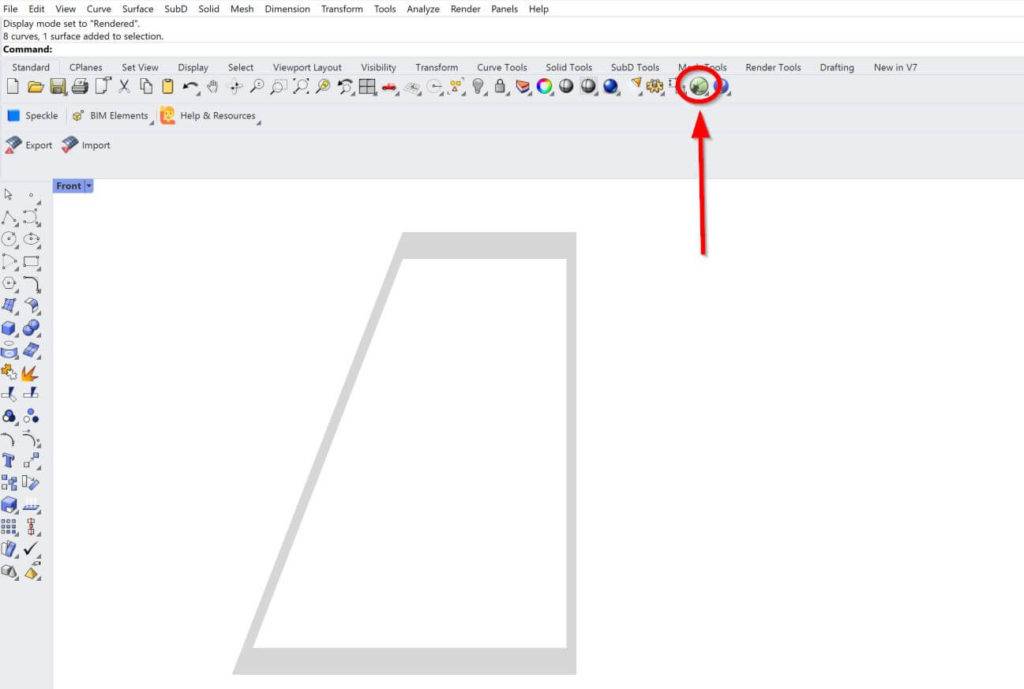
2. We then open Grasshopper.

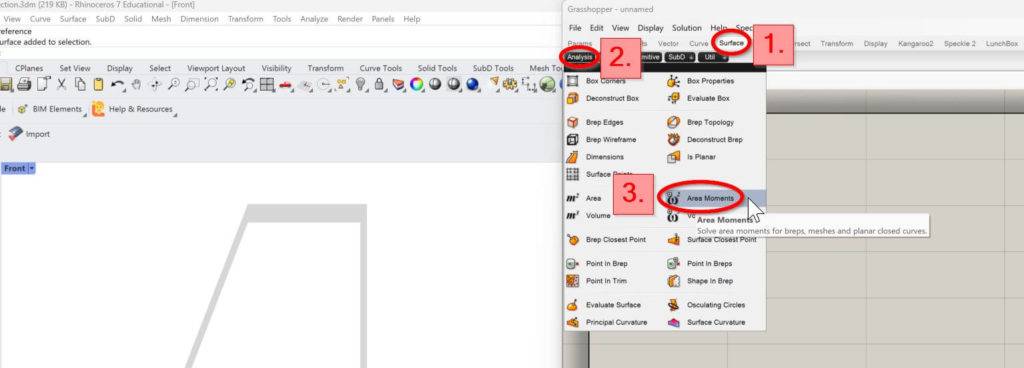
3. In Grasshopper, we click on Surface, Analysis and Area Moments.

4. Right click on Geometry of the component, click on Set one Geometry and select the surface of the Cross-section.

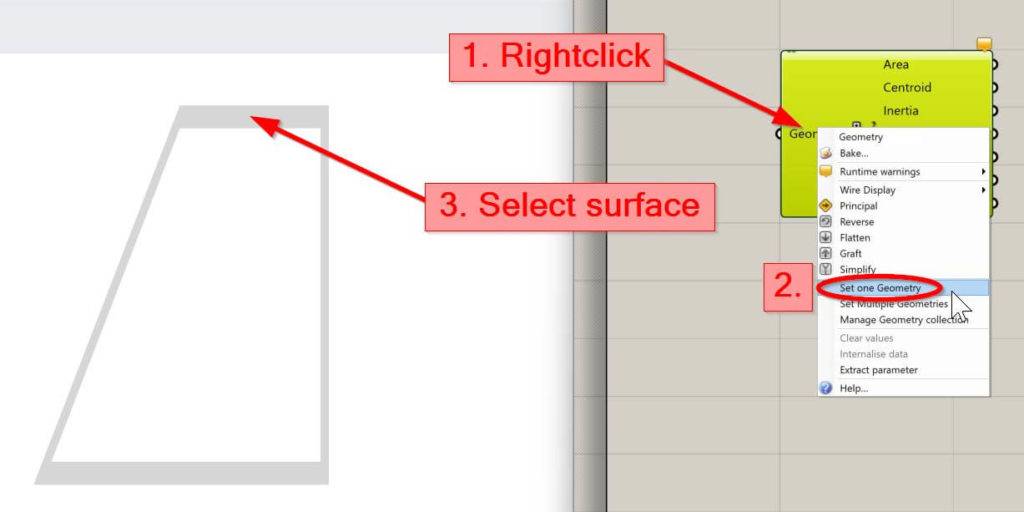
5. Connect a panel with the output of the Area Moments component to see the result.

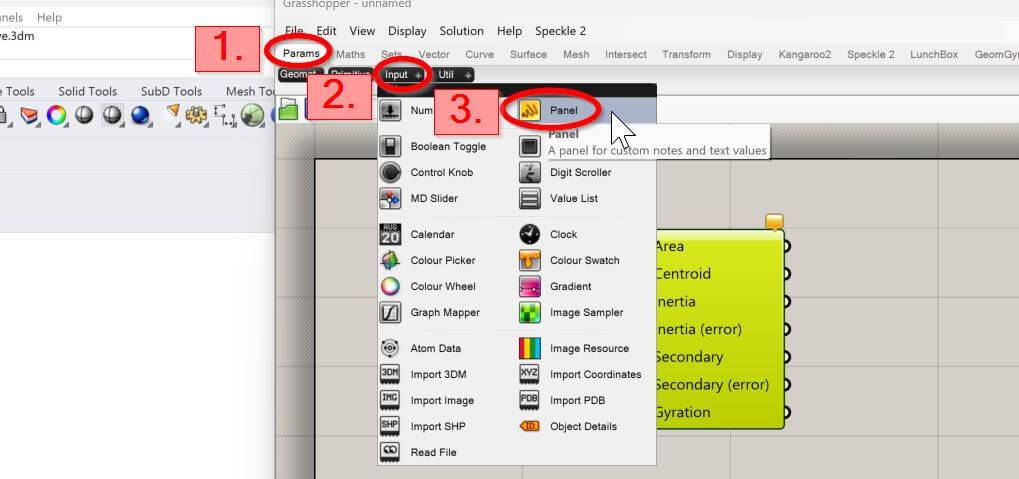
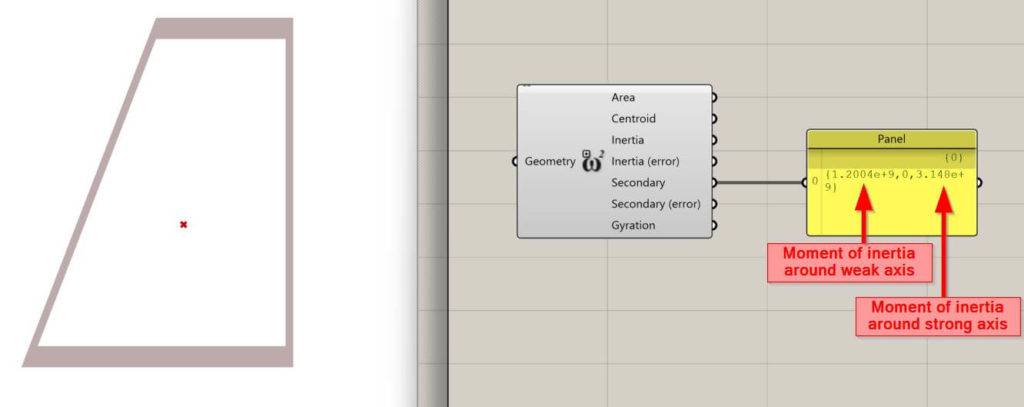
Now, we just connect the area output with the panel input, and we can see the calculated Moment of inertia.

❗Be careful, because the third value is the moment of inertia around the strong axis, while the first value is around the weak axis.

6. Right click on Centroid and click on Bake

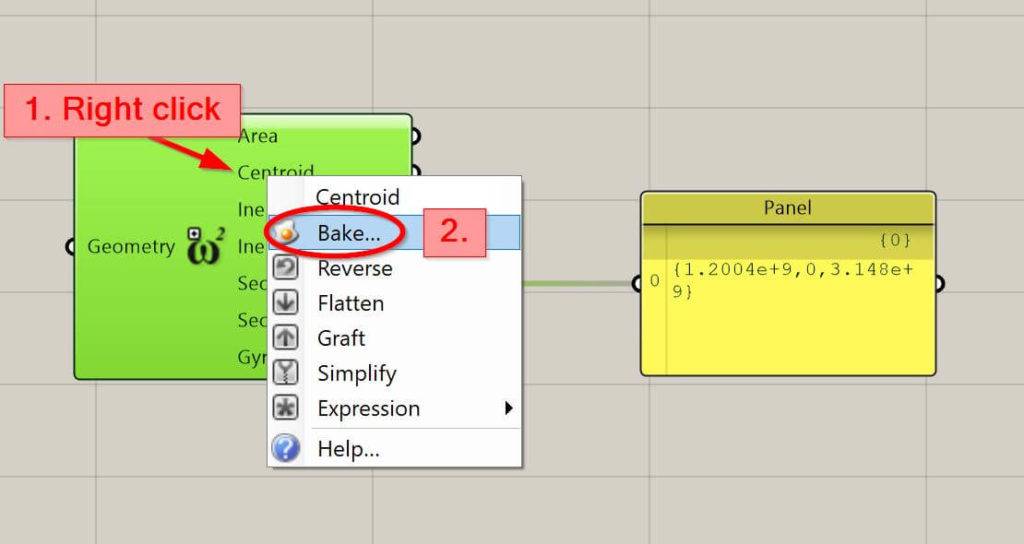
Now, the centroid is a point in Rhino.

7. We can now measure the distance from the centroid to the most outer fibres.

Click on Linear Dimension >> Vertical Dimension

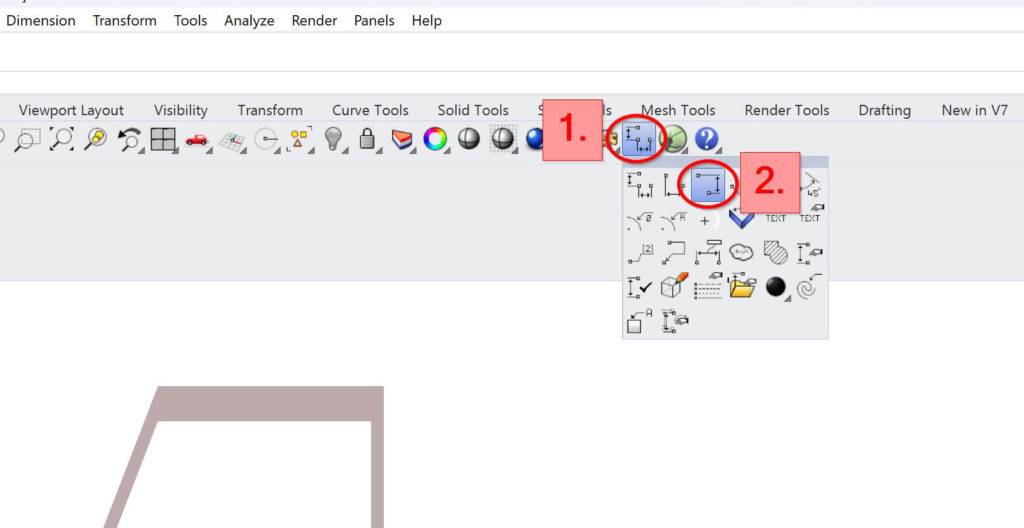
8. Click on the centroid point and a point on the top or bottom edge.

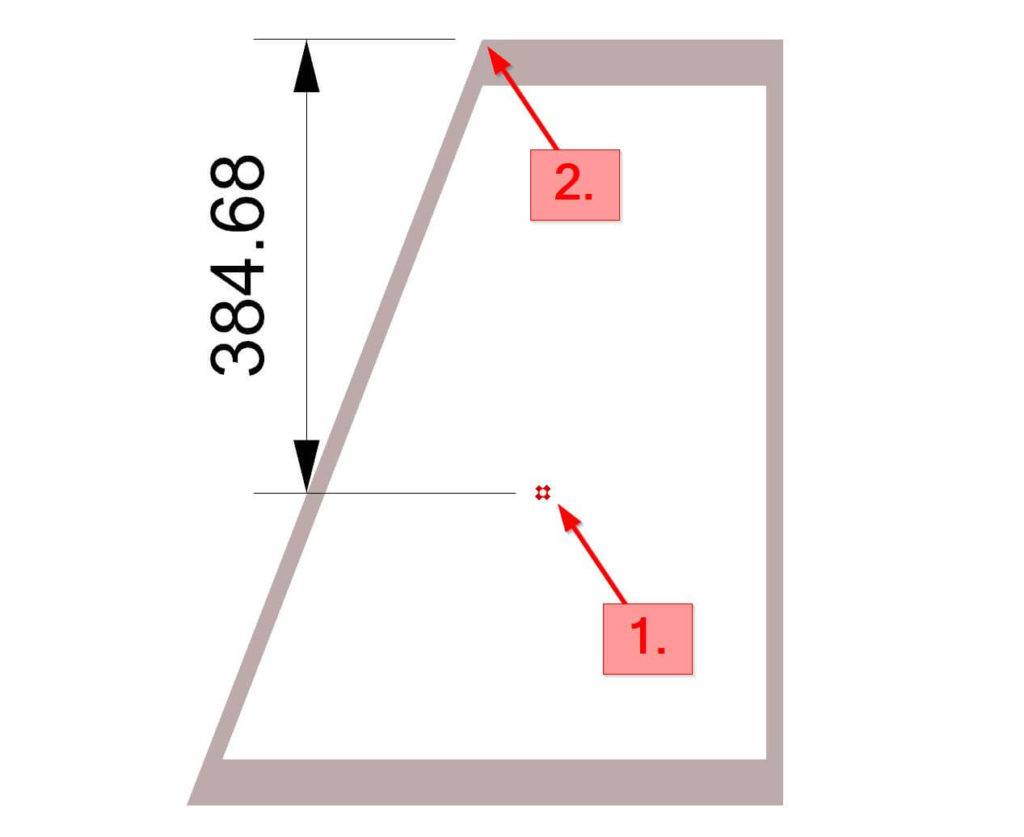
9. A tool like SMath can now be used to calculate the section modulus from the moment of inertia and distance from the neutral axis (384.68mm).⬇️⬇️

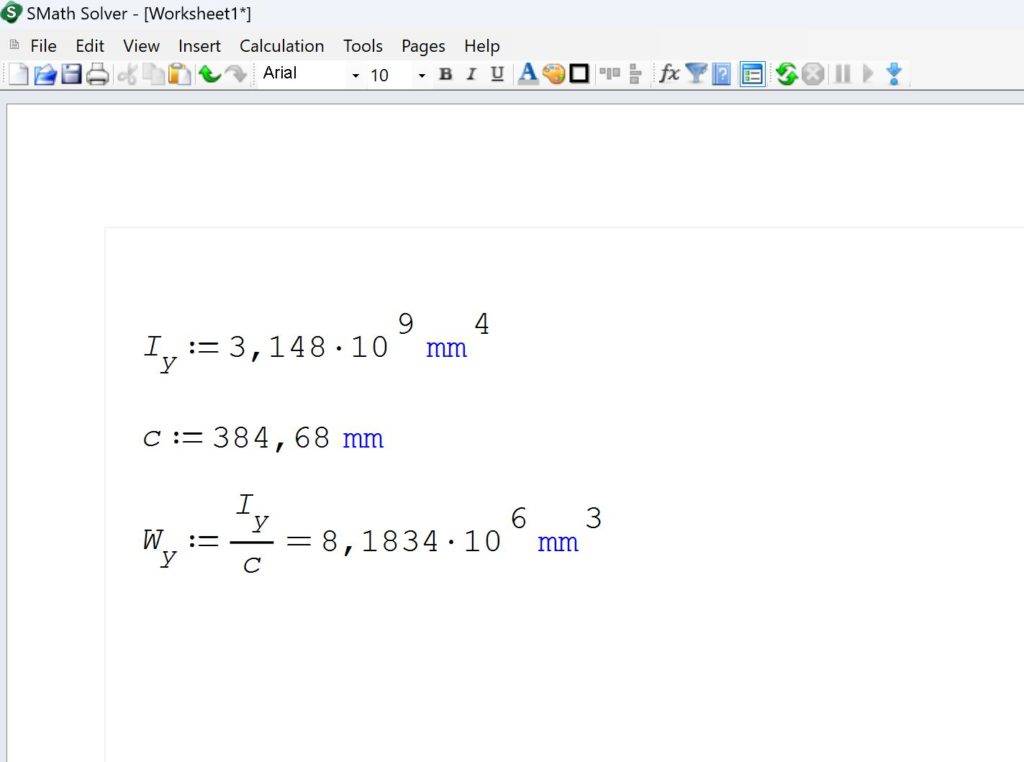
Isn’t that great?! And it would be even better if there was a component in Grasshopper that is able to calculate the section modulus automatically. In case you know of such a component, please let me know in the comments. ✍️✍️

Also, if you need a video tutorial for this, let us know.

Conclusion

Now, that you got an understanding of how to calculate the section modulus, you can learn about moment of inertia and cross-sectional area, because these parameters are also cross-sectional properties and used in engineering.

• Moment of inertia calculation
• Cross-sectional area calculation

If you want to learn where the section modulus and moment of inertia is used in structural engineering, then check out the following articles.📖📖

• Bending verification of a steel beam
• Lateral torsional buckling verification of a steel beam
• Timber flat roof beam design

I hope that this article helped you understand the section modulus calculation and how to go further from here. In case you still have questions.

Let us know in the comments below. ✍️✍️

Section Modulus FAQ