Unreinforced Masonry Shear Wall Design {2024}

Masonry shear walls are commonly used in residential family houses. They resist horizontal loads such as wind and seismic loads and transfer these loads down to the foundation.

In this guide, I’ll show, step-by-step, how you design unreinforced masonry shear walls.

Let’s get started. 🚀🚀

What Are Masonry Shear Walls?

Masonry shear walls or also called stabilizing walls are structural elements that resist lateral loads such as wind and seismic loads and transfer these horizontal loads down to the foundation.

There are 2 types of masonry shear walls:

1. Unreinforced shear walls

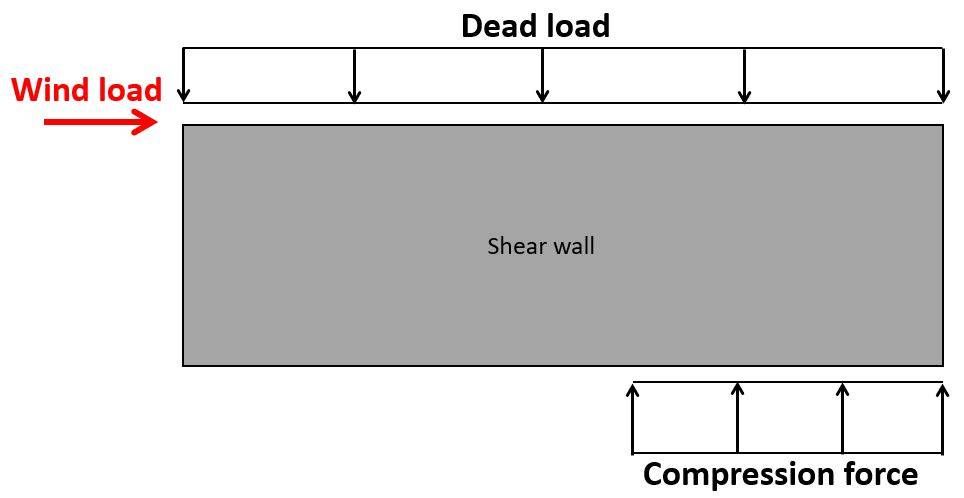
Unreinforced masonry shear walls can resist the horizontal loads by its own dead load. Overturning is verified and a vertical compression force/load is tranfered to the supporting floor. We structural engineers usually try to verify masonry shear walls without reinforcement, because it’s cheaper and easier to construct.

2. Reinforced shear walls

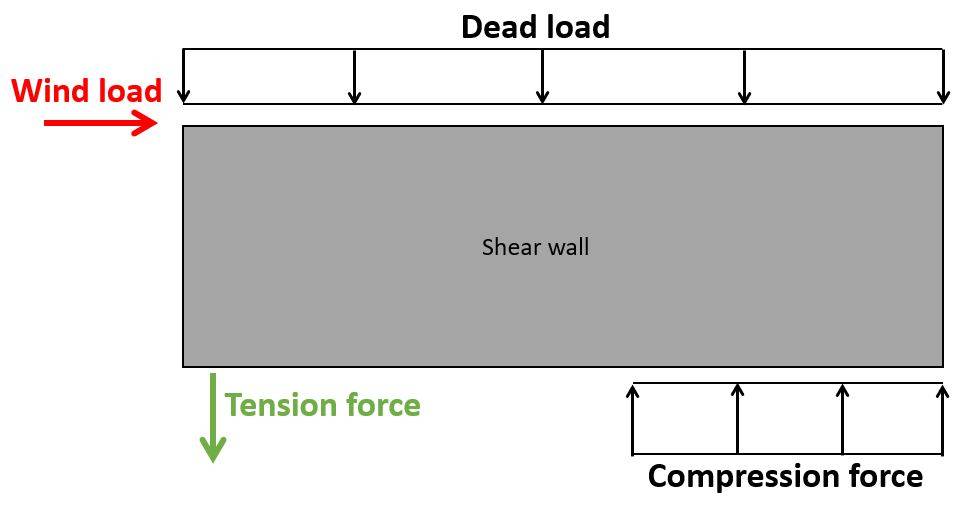
Reinforced masonry shear walls have reinforcement which anchors one side of the wall to the floor or wall below. If reinforcement is missing the wall would overturn.

As already said, we’ll design and verify an unreinforced shear wall in this tutorial.

Process of Unreinforced Shear Wall Design

Before we dive into the nerdy calculations, it’s good to get an overview of the steps that need to be taken in the design. 👇👇

There are many different types of masonry. In this tutorial, we’ll use clay units which are common in most countries.

1. Characteristic Loads

Shear walls have to withstand the horizontal loads acting on a building. However, the self-weight of the structural elements is acting on the walls at the same time, which is beneficial and increasing the resistance of the shear walls.

Therefore, we are also defining the dead load of the structural elements (g_k.inf = lower bound).

Lateral Wind Loads

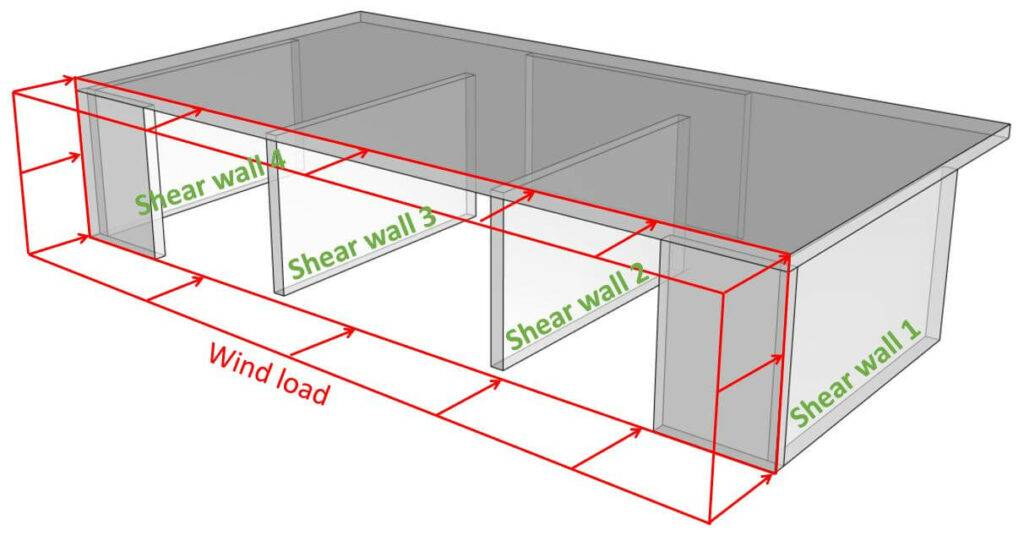
The horizontal loads are transferred from the facades through the floor slabs to the stabilizing walls. The shear walls need to withstand these horizontal wind loads and transfer the loads down to the foundations.

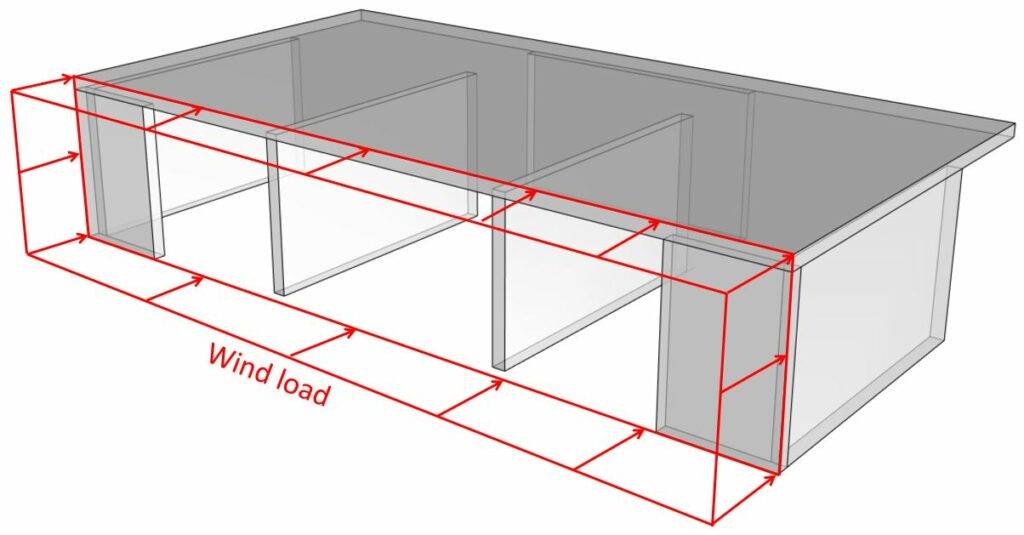
We are not calculating the wind loads in detail in this post, because we have written a step-by-step article that you can follow. 👇👇

Be aware that the following loads are assumptions and we didn’t calculate them.

Characteristic wind load area D	wk.D = 1 kN/m2
Characteristic wind load area E	wk.E = 0.6 kN/m2

The wind loads for areas A, B and C are neglected, because they are of the same magnitude on both transverse facades and therefore don’t influence the stabilizing system for a rectangular building.

Distribution of Wind Loads

1. The horizontal wind loads act perpendicular on the facade (see picture above)
2. The facade elements then transfer the load to the floor diaphragms. The load w_k.l on the floor diaphragm is calculated as:

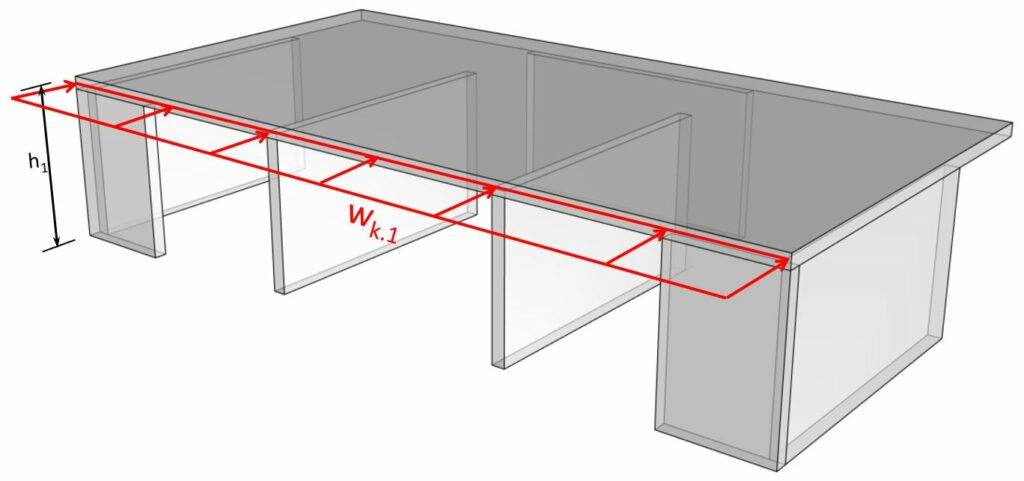
Let’s use the following values for h₁:

h1

4 m

We then find the line loads on the floor diaphragms:

Wind load on 1st floor / roof diaphragm

$w_{k.1} = (w_{k.D} + w_{k.E}) \cdot \frac{h_1}{2} = 3.2 kN/m$

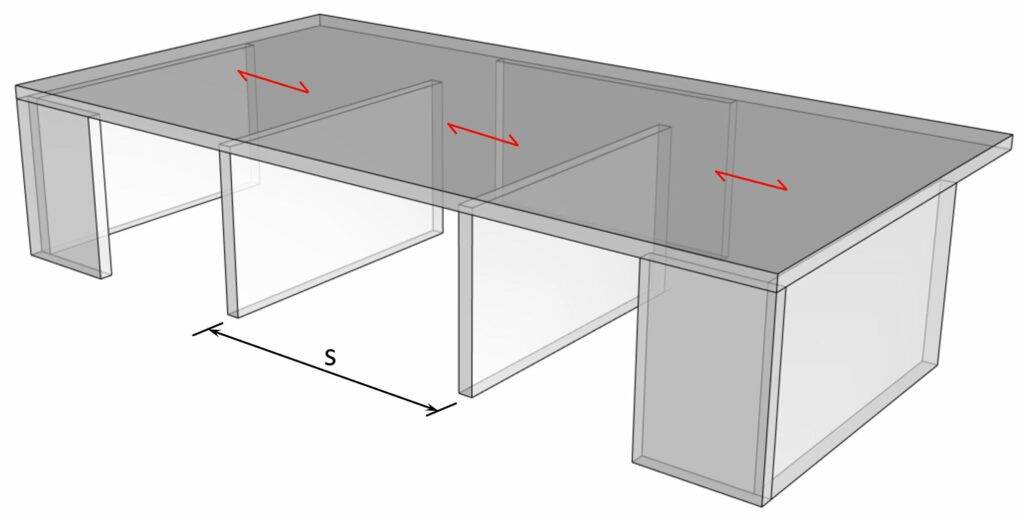
3. The wind loads travel through the floor diaphragm and to the shear walls, assuming the diaphragm is stiff enough. The load distribution is done elastically for in-situ or precast concrete floors with masonry walls. This is, however, a topic for another blog post.
As all 4 transverse shear walls are of the same length and stiffness, each wall takes up 25% of the entire wind load (-> w_k.w).

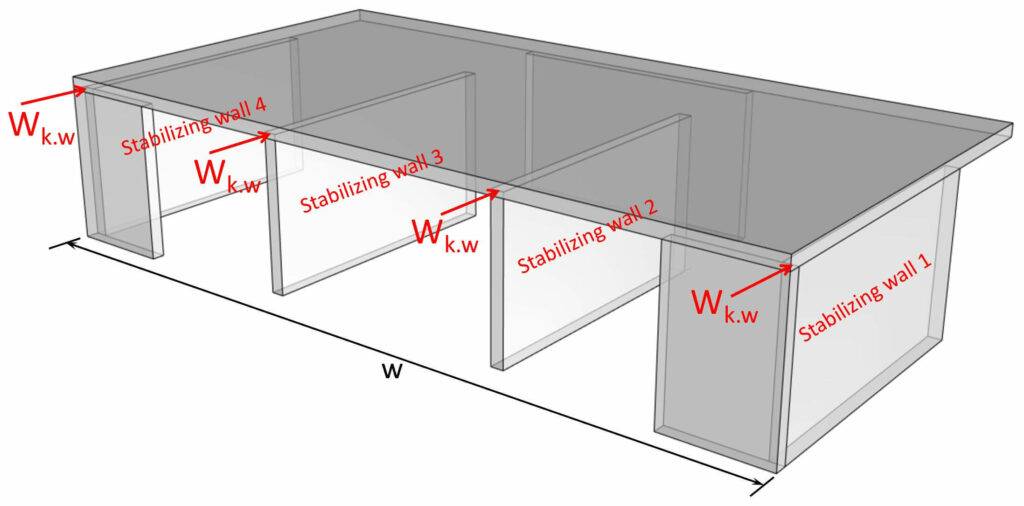
Let’s set the width of the building to: 👇👇

$$w = 15 m$$

Now, this also has to be done for the floor and walls above if there are other floors. In general for every floor and every wall of a building.

Wind point load on walls – ground floor

$W_{k.w.1} = w_{k.1} \cdot \frac{w}{4} = 12.0 kN$

Vertical Dead Load

Additionally, to the horizontal load, the vertical dead load also needs to be considered, as the dead load always acts on the walls.

Later in the calculation, we’ll see that the bigger the dead load, the better the stabilization of the wall.

In our design, the transverse stabilizing walls also support the one-way spanning concrete slabs.

Therefore, we’ll include the dead load of the stabilizing walls itself and the concrete slabs.

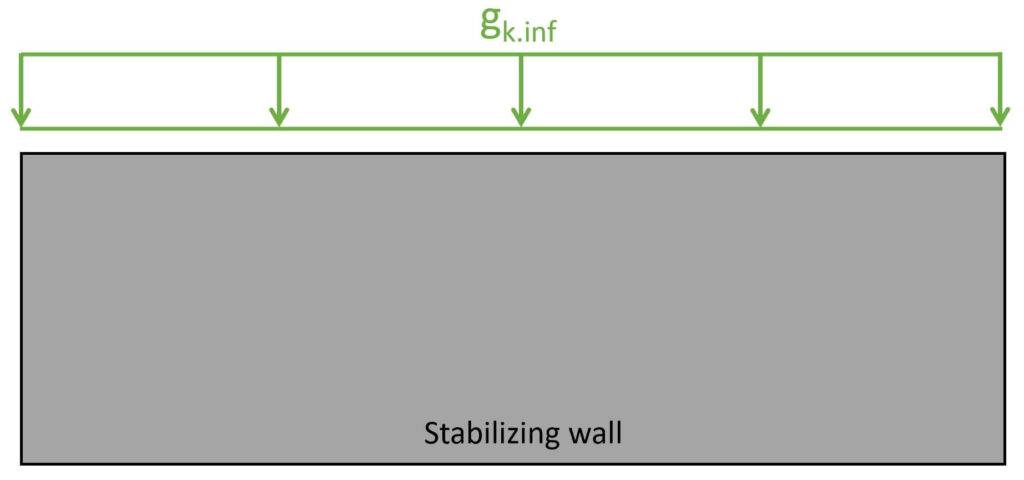
Dead load of concrete slab (t=200 mm)	$g_{k.h} = 25 kN/m^3 \cdot 0.2 m = 5 kN/m^2$
Density of masonry (Porotherm 25-38 EFH)	$\rho_m = 7.45 kN/m^3$
Thickness of walls	$t = 250 mm$
Dead load on stabilizing wall (walls 1 and 4) – ground floor	$g_{k.inf.0} = \rho_m \cdot t \cdot h_1 + g_{k.h} \cdot \frac{5m}{2} = 20.0 kN/m$

2. Load Combinations

Load combinations combine several load cases and multiply the characteristic loads with safety factors.

Luckily, we have already written an extensive article about what load combinations are and how we use them.

In case you need to brush up on it or want to check how we derived the safety factors, you can read the blog post here.

The dead load will not have the typical factor of 1.35 but instead 1.0 according to EN 1990 Table A1.2 (B). This is because the dead load acts favourable, which means that the bigger the dead load, the higher the load bearing capacity.

For the design of the stabilizing wall, we’ll look at the following ULS load combinations. 👇👇

ULS load combinations

LC1	$1.0 \cdot g_{k.inf} + 1.5 \cdot w_k$
LC2	$1.35 \cdot g_{k.sup} + 1.5 \cdot w_k + 1.5 \cdot \psi_0 \cdot q_k$

Now, LC1 will be leading for the verification of the stabilizing wall. That’s why, we’ll continue only with LC1. However, LC2 will lead to compression stresses at the bottom of the walls. So to verify the joint, you should also consider LC2.

Design wind load – ground floor	$W_{d.w.1} = 1.5 \cdot W_{k.w.1} = 18 kN$
Design dead load – ground floor	$g_{d.inf.1} = 1.0 \cdot g_{k.inf.1} = 20.0 kN/m$

3. Geometry Of The Walls

We have already defined the heights of the stabilizing walls as h₁.

We set the length to l = 4m.

4. Masonry Properties

We’ll use clay masonry units (Porotherm 25-38 EFH) and mortar strength class M5.

Initial shear strength (EN 1996-1-1 Table 3.4)	$f_{vk0} = 0.2 N/mm^2$
Group (from Porotherm datasheet)	2
Normalised mean compressive strength (from Porotherm datasheet)	$f_{b} = 10.2 MPa$
Max. shear strength (Danish Annex)	$f_{vk.max} = min(k_m \cdot f_b ; 1.5 MPa) = 0.71 MPa$
Limit value of shear strength (Danish Annex)	$f_{vlt} = 1.5 MPa$
Partial factor for shear strength of masonry (Danish Annex)	$\gamma_{c.v} = 1.7$
Friction coefficient (Danish Annex)	$\mu = 0.6$
Partial factor for friction (Danish Annex)	$\gamma_{c.f} = 1.3$
Partial factor for compressive strength (Danish Annex)	$\gamma_{c.c} = 1.6$
Constant (EN 1996-1-1 Table 3.3)	$K = 0.45$
Compressive strength of mortar M5 (general purpose mortar)	$f_m = 5 MPa$
Characteristic compressive strength of masonry (EN1996-1-1 (3.2))	$f_k = K \cdot f_b^{0.7} \cdot f_m^{0.3} = 3.7 MPa$
Design compressive strength of masonry	$f_d = \frac{f_k}{\gamma_{c.c}} = 2.32 MPa$

5. ULS Verification Of A Wall Subjected To A Concentrated Load

In this verification, we check that the localised compression stresses/forces N in the bottom of the wall can be taken up by the masonry.

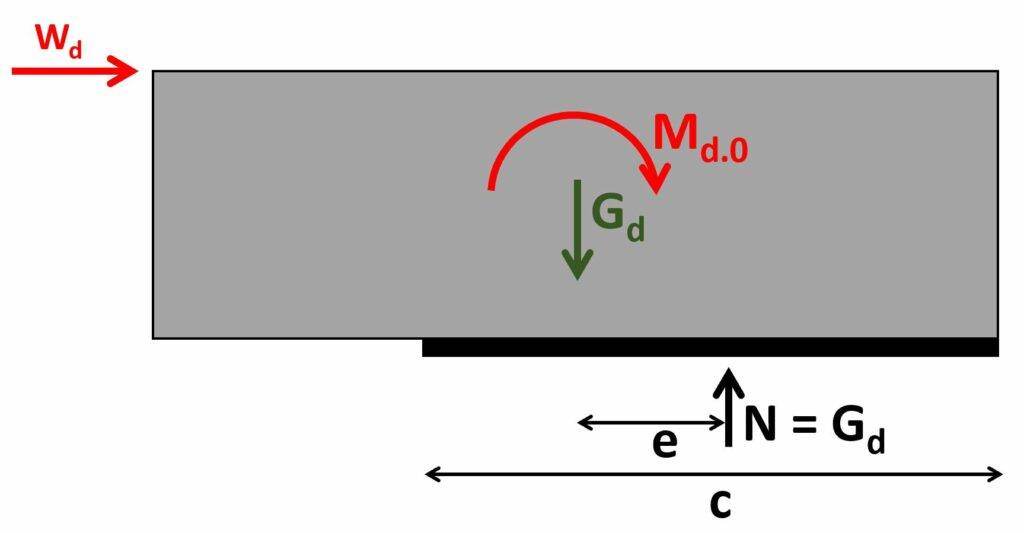
Lateral wind load on wall	$W_{d.1} = 18 kN$
Vertical design load	$p_{d} = g_{d.inf.1} = 20 kN/m$
Design bending moment at the bottom of the wall	$M_d = W_{d.1} \cdot h_1 = 72 kNm$
Eccentricity of load	$e = \frac{M_{d.0}}{p_d \cdot l} = 0.9m$
Check that eccentric load is within the wall	$e < l/2 = 1$
Width of compression zone	$c = 2 \cdot (\frac{l}{2} – e) = 2.2 m$
Compression stress in compression zone	$N_d = \frac{M_d}{c \cdot e \cdot t} = 0.15 MPa$
Utilisation	$\eta = \frac{N_d}{f_d} = 0.06$

6. ULS Verification Of The Shear Strength Of The Wall

Shear strength of shear wall	$f_{vd} = min(\frac{f_{vk0}}{\gamma_{c.v}} + 0.4 \cdot N_d; f_{vd.max}) = 0.18 MPa$
Shear resistance of unreinforced masonry wall (EN 1996-1-1 (6.13))	$V_{Rd} = f_{vd} \cdot t \cdot c = 96.7 kN$
Utilisation	$\eta = \frac{W_d.1}{V_Rd} = 0.19$

7. ULS Verification Of Sliding Of The Wall

Sliding resistance of unreinforced masonry wall	$H_{Rd} = \frac{\mu}{\gamma_{c.f}} \cdot P_d \cdot l = 36.9 kN$
Utilisation	$\eta = \frac{W_d.1}{H_Rd} = 0.49$

Conclusion

Et voilà, the unreinforced masonry shear wall is verified and dimensioned. 💯💯

If you are new to structural design, then check out more of our design tutorials where you can learn how to design elements such as: 👇👇

• Design reinforced concrete beams
• Reinforced concrete column design
• Punching shear design of a flat slab

But now, I would like to hear from you: Are you designing stabilizing walls for a uni project? Or are you renovating your own house? Tell us a bit about the structure, as we all want to learn from each other.✍️