Fillet Weld Design {2024 Engineering Guide}

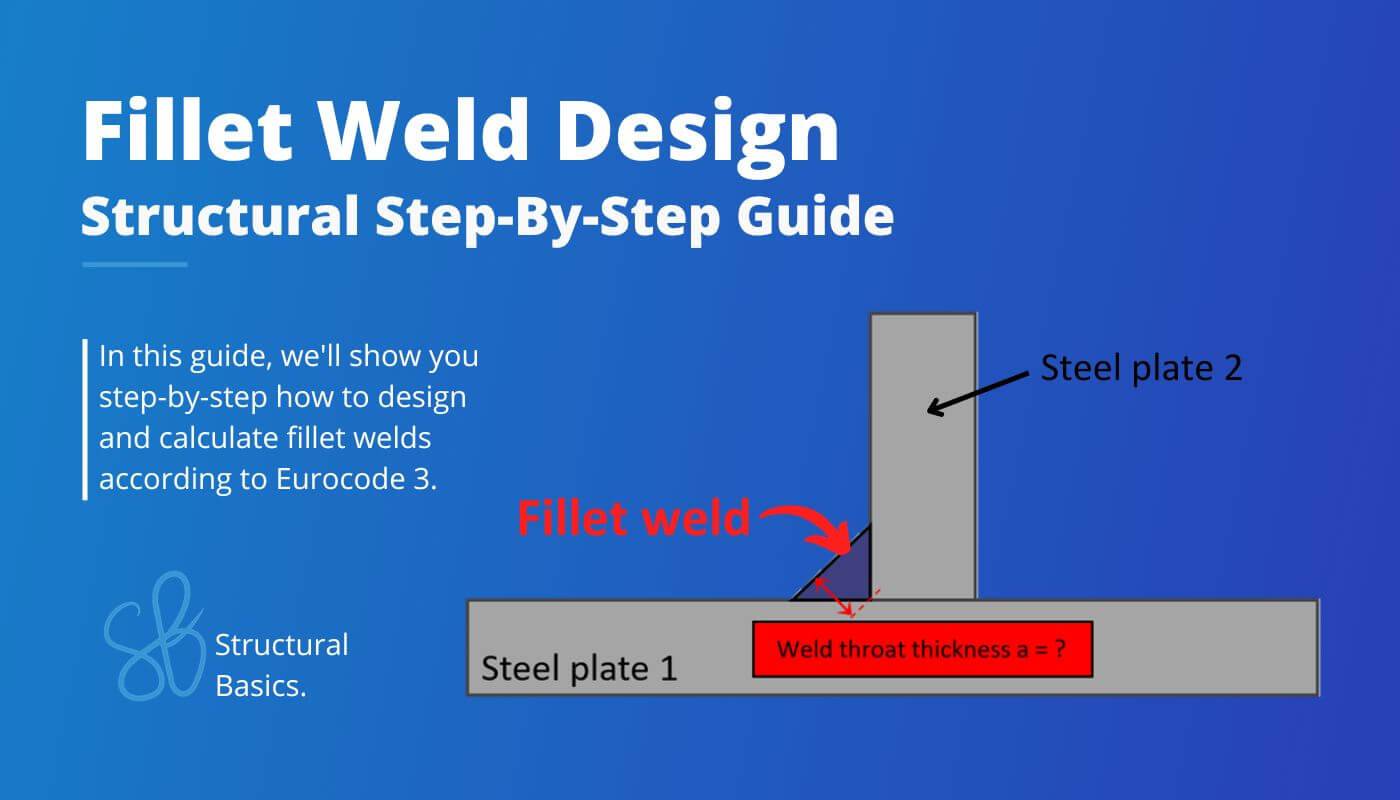
Fillet welds are one of the most common types of welds.

In this article, we’ll show you step-by-step with an example structure how to design and calculate them.

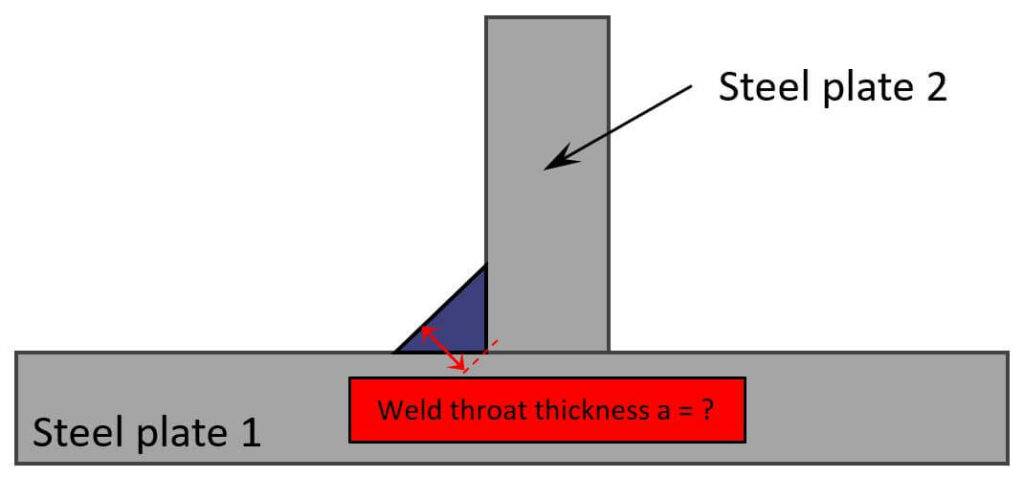
So let’s get started.

Design Resistance Of Fillet Welds

According to Eurocode EN 1993-1-8 4.5.3.1, either the directional method or the simplified method should be used to calculate the bearing capacity of fillet welds.

We’ll explain both in the following.

Directional Method

In the directional method, the forces acting on the weld are translated into force components parallel and transverse to its longitudinal axis and normal and transverse to its throat plane (EN 1993-1-8 4.5.3.2).

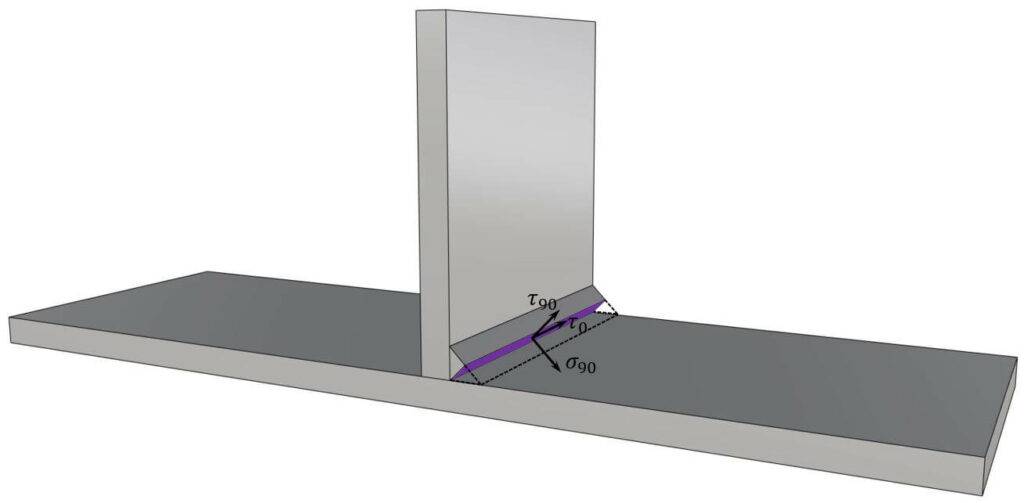
The fillet weld verifies if the following 2 criteria are satisfied (EN 1993-1-8 (4.1):

Criteria 1:

$$\sqrt{\sigma_{90}^2 + 3 (\tau_0^2 + \tau_{90}^2)} \le \frac{f_u}{\beta_w \gamma_{M2}}$$

Criteria 2:

$$\sigma_{90} \le 0.9 \frac{f_u}{\gamma_{M2}}$$

Ok, so now let’s break down its components.

Stresses $\sigma_{90}$, $\tau_{90}$ and $\tau_{0}$

The stresses in the weld are calculated from the internal forces acting in the plate:

• Bending moment M
• Normal force N
• Shear force V

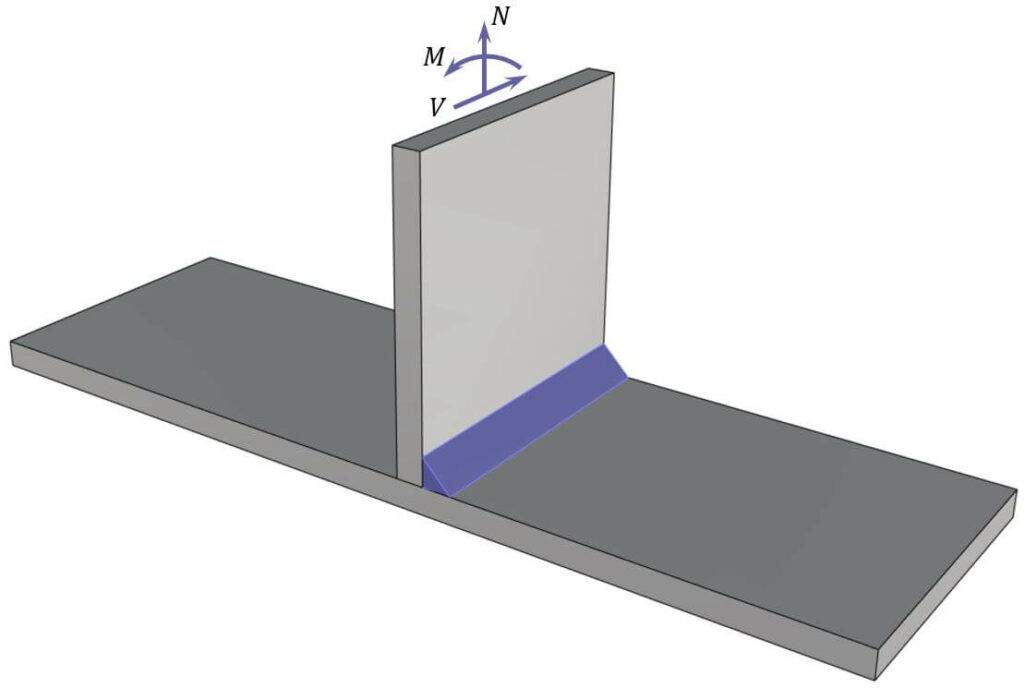
$$\sigma_{90} = \frac{N}{2 \cdot l_{eff} \cdot a \cdot \sqrt{2}} + \frac{M}{2 \cdot l_{eff}^2 \cdot a/6 \cdot \sqrt{2}}$$

$$\tau_{90} = \sigma_{90}$$

$$\tau_{0} = \frac{V}{2 \cdot l_{eff} \cdot a}$$

With,

$l_{eff}$	Effective length of the weld
$a$	Throat thickness

Let’s continue by checking out the steel property parameters that we also need for the verification. 💯💯

Steel Properties

$f_u$	Ultimate tensile strength of the weaker of the 2 steel plates. You can find the ultimate tensile strengths in EN 1993-1-1 Table 3.1. For a S235 steel fu = 360 N/mm2
$\beta_w$	Correlation factor which depends on the steel strength. You can determine the value from EN 1993-1-8 Table 4.1. For a S235 steel $\beta_w$ = 0.8.
$\gamma_{M2}$	Safety factor. You can determine the general value from EN 1993-1-1 6.1. But usually every country has its own values. So make sure to check your national annex.

Later in this article, we’ll show a step-by-step calculation example.

Simplified Method

The second method that Eurocode recommends is the simplified method. In textbooks, it’s said that this method is conservative.

In this method, the following criteria has to be fulfilled:

$$F_{w.Ed} \le \frac{f_u \cdot a}{\sqrt{3} \cdot \beta_w \cdot \gamma_{M2}}$$

With

$F_{w.Ed}$	Resultant of all design forces per unit length
$f_u$	Ultimate tensile strength of the weakest of the 2 steel plates. For more information, see table above.
$\beta_w$	Correlation factor, which depends on the steel strength. For more information, see table above.
$\gamma_{M2}$	Safety factor. For more information, see table above.

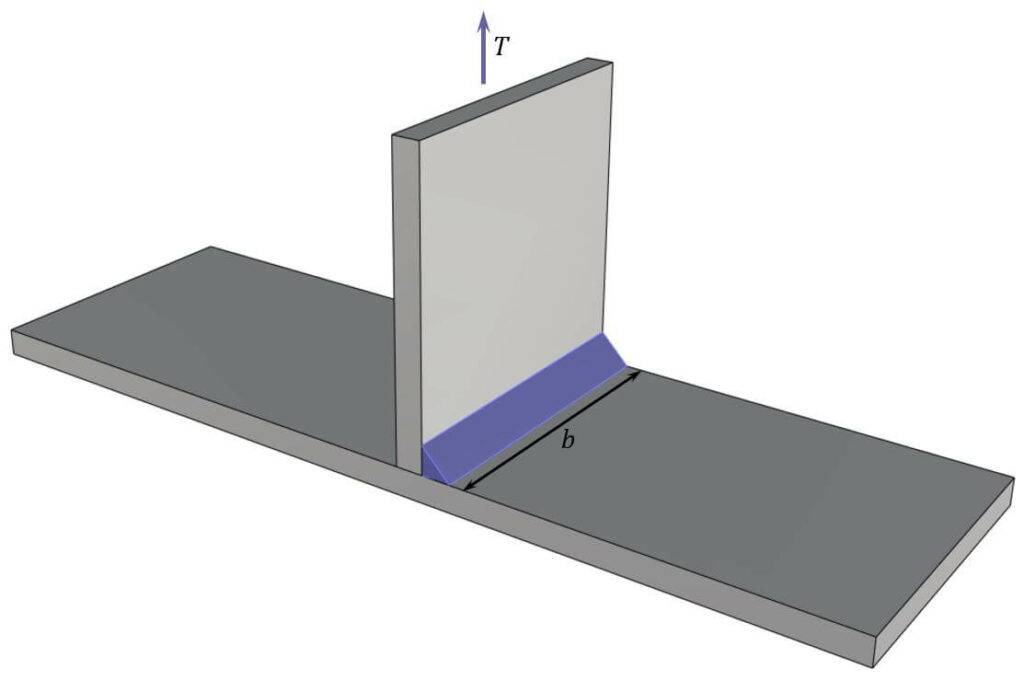
For the following weld that is only exposed to a tension force, $F_{w.Ed}$ is calculated as

$$F_{w.Ed} = \frac{T}{b}$$

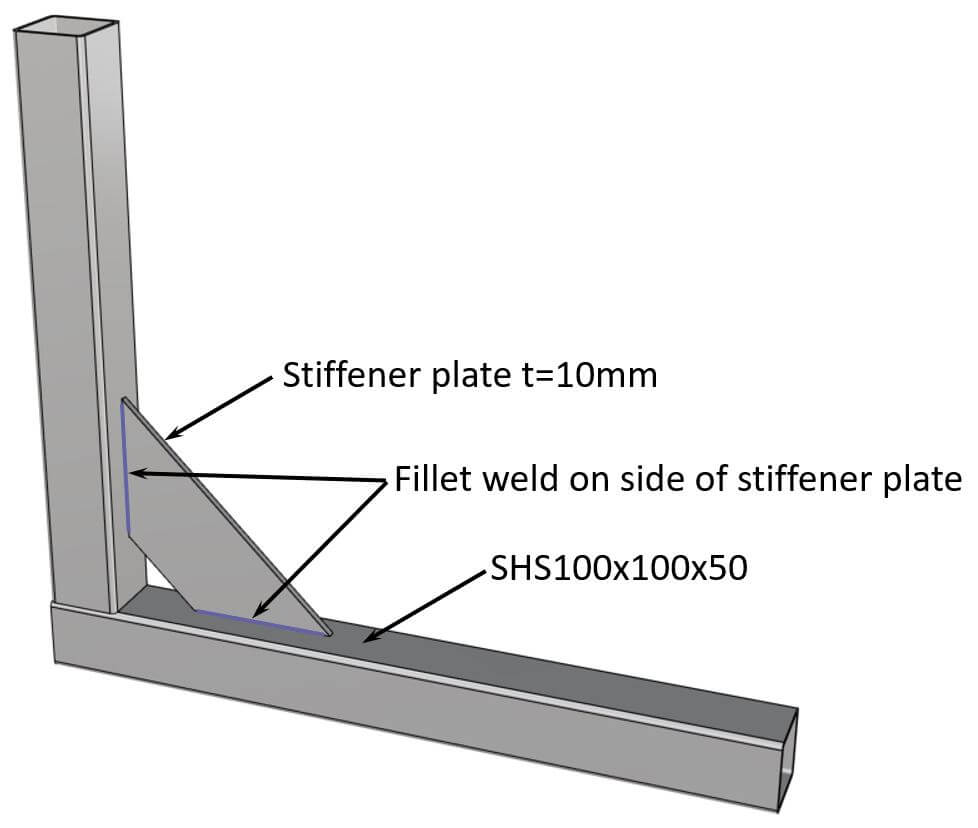
Example Calculation With Directional Method

For the following example structure, a fillet weld makes most sense, because the plates are easy to weld from both sides.

Loads/Internal forces

We calculate the fillet weld for the following internal forces:

Design bending moment	$M_{d} = 0.9 kNm$
Design axial force	$N_{d} = 15 kN$
Design shear force	$V_{d} = 0.4 kN$

Geometry of the fillet weld

Throat thickness	$a = 3 mm$
Length of the weld	$l_w = 80mm$

Material data

Ultimate tensile strength	$f_{u} = 360 MPa$
Correlation factor	$\beta_{w} = 0.8$
Partial safety factor	$\gamma_{M2} = 1.25$

Verification

Stresses in weld	$\sigma_{90} = \frac{N/2}{2 \cdot l_{eff} \cdot a \cdot \sqrt{2}} + \frac{M}{2 \cdot l_{eff}^2 \cdot a/6 \cdot \sqrt{2}} = 145.8 MPa$ $\tau_{90} = \sigma_{90} = 145.8 MPa$ $\tau_{0} = \frac{V/2}{2 \cdot l_{eff} \cdot a} = 0.83 MPa$
Resulting stress	$\sigma_{eff} = \sqrt{\sigma_{90}^2 + 3 \cdot (\tau_{90}^2 + \tau_{0}^2)} = 291.7 MPa$
Resistance stresses	$\sigma_{Rd.1} = \frac{f_u}{\beta_w \cdot \gamma_{M2}} = 360 MPa$ $\sigma_{Rd.2} = 0.9 \frac{f_u}{\gamma_{M2}} = 259.2 MPa$
Utilization	$\eta = \frac{\sigma_{eff}}{\sigma_{Rd.1}} = 81 \%$ $\eta = \frac{\sigma_{90}}{\sigma_{Rd.2}} = 56.3 \%$

Example Calculation With Simplified Method

We’ll use the same example structure as for the directional method.

Loads/Internal forces

The internal forces are the same as for the directional method.

Design bending moment	$M_{d} = 0.9 kNm$
Design axial force	$N_{d} = 15 kN$
Design shear force	$V_{d} = 0.4 kN$

Geometry of the fillet weld

Throat thickness	$a = 3 mm$
Length of the weld	$l_w = 80mm$

Material data

Ultimate tensile strength	$f_{u} = 360 MPa$
Correlation factor	$\beta_{w} = 0.8$
Partial safety factor	$\gamma_{M2} = 1.25$

Verification

Moment of inertia (weld)	$I_y = 2 \cdot \frac{l_w^3}{12} \cdot a = 2.56 \cdot 10^5 mm^4$
Section modulus	$W_y = \frac{I_y}{l_w/2} = 6.4 \cdot 10^3 mm^3$
Stresses in weld	$\sigma_{N} = \frac{N_d}{2 \cdot l_{w} \cdot a} + \frac{M_d}{W_y} = 171.9 MPa$ $\tau_{v} = \frac{V_d}{2 \cdot l_{w} \cdot a} = 0.83 MPa$
Resulting stress	$F_{w.Ed} = \sqrt{\sigma_{N}^2 + \tau_{v}^2} = 171.9 MPa$
Resistance stress	$\sigma_{Rd} = \frac{f_u}{\sqrt{3} \cdot \beta_w \cdot \gamma_{M2}} = 207.9 MPa$
Utilization	$\eta = \frac{F_{w.Ed}}{\sigma_{Rd}} = 82.7 \%$

As we can see, this method has a higher utilization as the directional method.

Conclusion

Et voilà, the fillet weld is verified and dimensioned. 💯💯

That was a quick verification, wasn’t it?

If you are new to structural design, then check out more of our design tutorials where you can also learn how to design other steel, concrete and wood elements such as

• Design of timber roof beams
• Reinforced concrete beam design
• Steel column design

But now, I would like to hear from you: Have you already designed a fillet weld in university or at your work? Tell us a bit about the structure, as we all want to learn from each other.