Statically Determinate & Indeterminate Structures

ByLaurin Ernst Updated
Statically determinate and indeterminate structures differences degree of indeterminancy with examples

Calculating internal forces by hand is one of the first things Civil engineering students learn at university.

But internal forces can only be calculated in the simple way with the 3 equilibrium equations if the structure is Determinate.

If a structure is statically Indeterminate, then more complicated methods need to be used to calculate Moments, reaction, shear and axial forces.

So in this article, we’ll show, what statically determinate and indeterminate structures are and how to calculate the degree of indeterminacy for different structures.

But now, let’s get started.

🙋‍♂️ What’s the difference between Internal and External Determinate Structures?

Before we explain what statically determinate structures are, we first have to mention that when we talk about determinacy & indeterminacy in this post, then we mean Internal Determinacy, instead of External.

Explanation

External (In)determinacy:

The reaction/support forces in an externally statically determinate structure can be calculated by the 3 Equilibrium equations. If the reaction components can’t be calculated, then the structure is externally statically indeterminate.

Internal (In)determinacy:

Compared to External determinacy, the internal forces (Moment, Shear & Normal force) can be calculated by the 3 Equilibrium equations additionally to the reaction/support forces in an Internally Statically Determinate Structure. If the internal forces and reaction components can’t be calculated, then the structure is Internally Indeterminate.

So what’s the Difference?

While in Externally & Internally Determinate structures the reaction forces can be calculated by the 3 Equilibrium equations, the Internal forces can only be calculated in Internally Determinate structures.

When we talk about statically determinate structures in this post, then we mean Internally determinate structures.

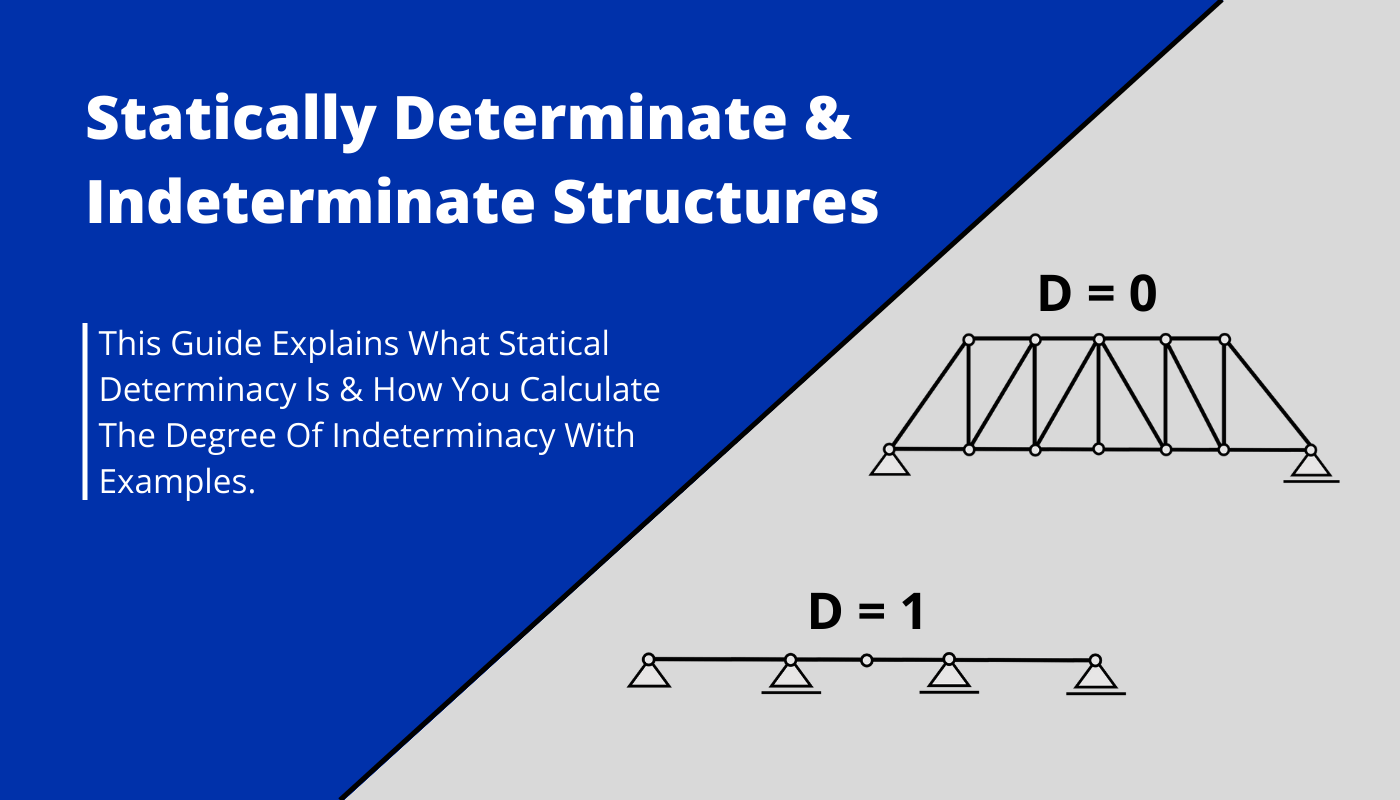
❔ What is a statically determinate structure?

Statically determinate structures are structures in which the reaction forces and the internal forces can be calculated by the 3 Equilibrium equations.

Vertical equilibrium: $\sum V = 0$

Horizontal equilibrium: $\sum H = 0$

Moment equilibrium: $\sum M = 0$

Examples of statically determinate structures are:

  • Simply supported beam
  • Cantilever beam
  • Column (roller + pin support)
  • 3-hinge arch
  • Truss (Not all trusses)
Simply supported beam. Example of a statically determinate structure. 3 Reaction forces.
Simply supported beam. Example of a statically determinate structure. 3 Reaction forces.
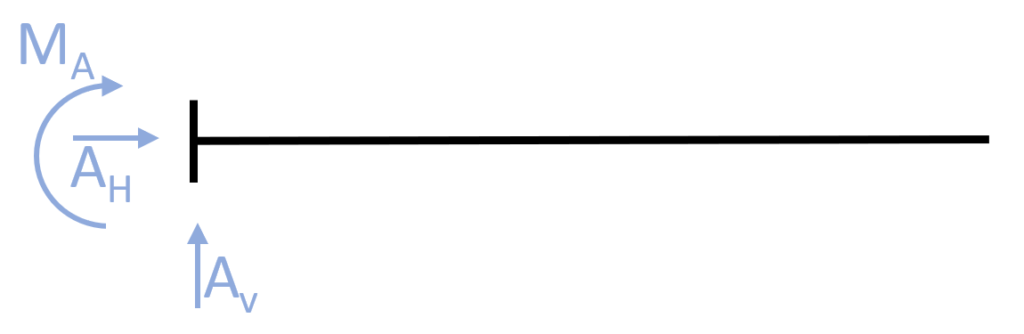
Cantilever beam. Example of a statically determinate structure. 3 Reaction forces.
Cantilever beam. Example of a statically determinate structure. 3 Reaction forces.
Column. Example of a statically determinate structure.

🤔 What is a statically indeterminate structure?

Statically Indeterminate Structures are structures in which the reaction forces and the internal forces CAN NOT be calculated by the 3 Equilibrium equations.

When trying to solve the 3 Equilibrium equations for an indeterminate structure, you will experience that you have 4 or more Unknowns (Reaction & Internal forces) for 3 equations.

Examples of statically indeterminate structures are:

  • Continuous beams
  • Frames
  • Some Trusses
Rigid frame as example of a statically indeterminate structure.
Rigid frame as example of a statically indeterminate structure. 6 Reaction forces.

🧮 Determinacy Equations

Beams & Frames [1]:

The degree of indeterminacy D for beams and frames is calculated as

$$ D = 3n + r – 3j – c$$

Where

  • n = amount of members
  • r = external restraints (number of support reactions)
  • j = number of joints
  • c = number of releases introduced (internal hinges)

Let’s have a look at some examples.

3 span continuous beam

Statical determinacy of a 3 span continuous beam.
Statical determinacy calculation of a 3 span continuous beam.

$$ D = 3 \cdot 3 + 5 – 3 \cdot 4 – 0 = 9 + 5 – 12 = 2 $$

D = 2 means that the structure is statically indeterminate to the 2nd degree. The reaction & internal forces CAN NOT be calculated by the 3 Equilibrium equations.

3 span continuous beam with hinge

Statical determinacy calculation of a 3 span continuous beam with a hinge.

$$ D = 3 \cdot 4 + 5 – 3 \cdot 5 – 1 = 12 + 5 – 15 – 1 = 1 $$

D = 1 means that the structure is statically indeterminate to the 1st degree. The reaction & internal forces CAN NOT be calculated by the 3 Equilibrium equations.

Trusses [1]:

The degree of indeterminacy D for trusses is calculated as

$$ D = n + r – 2j $$

Where

  • n = amount of members
  • r = external restraints (number of support reactions)
  • j = number of joints

Let’s have a look at some examples.

Warren Truss

Statical determinacy of a Warren Truss
Statical determinacy of a Warren Truss

$$ D = 11 + 3 – 2 \cdot 7 = 0 $$

D = 0 means that the structure is statically determinate. The reaction & internal forces can be calculated by the 3 Equilibrium equations.

Howe Truss

Statical determinacy of a Howe Truss

$$ D = 21 + 3 – 2 \cdot 12 = 0 $$

D = 0 means that the structure is statically determinate. The reaction & internal forces can be calculated by the 3 Equilibrium equations.

If you are new to structural design, then check out our design tutorials where you can learn how to use the calculated bending moments and shear forces to design structural elements such as

But now I would like to know from you, have you understood the concept of Bending moment, shear and normal force? Because I remember, it took me almost my entire 1st semester to really understand how to calculate moments. So let us know in the comments✍️, if you want more detailed posts and how you learned the concept of Moments.

📃 References

[1]: Williams A. Ph.D., S.E., C.ENG. (2009) Structural Analysis

Similar Posts