Timber Truss Roof Design [A Structural Guide]

Designing a timber roof truss for a new building project can be challenging.

You not only have to consider all loads acting on the roof (snow, wind, dead and live load) and choose the type of truss.

But you also must know how to design timber elements and ensure the structure is structurally sound.

In this post, we’ll go through, step-by-step, how to calculate the internal forces like moment and axial forces.

We’ll also define a static system and dimension the elements of the truss roof according to the Timber Eurocode EN 1995-1-1:2004.

Not much more talk, let’s dive into it.

🙋‍♀️ What is a timber truss roof?

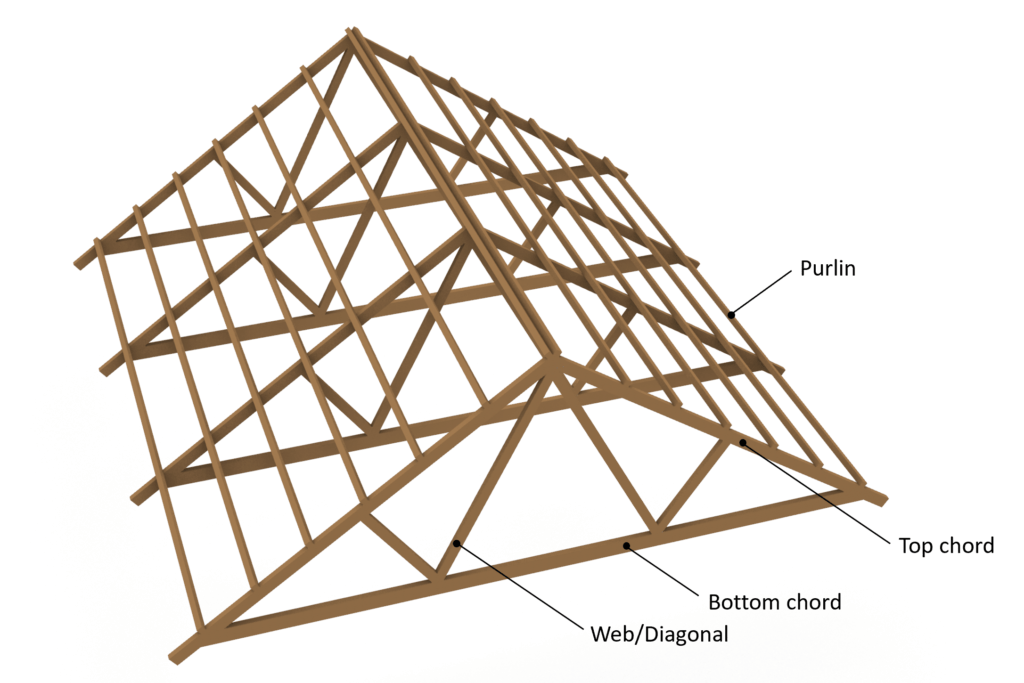
The truss roof is a structural roof system spanning between 2 supports and carrying loads like wind, snow and live load. Compared to other trusses, the truss roof is usually inclined from the supports towards the midpoint. It consists of top chord, bottom chord, diagonals and connections. Statically speaking are the top and bottom chords beams, acting in normal forces, shear forces and bending moments, while the diagonals, usually, act as bars and only take up normal forces.

Doing a little bit of research i found that the diagonals can also be called:

• webs
• tie (when in tension)
• strut (when in compression)

the top chord is sometimes called

• upper chord

and the bottom chord

• lower chord
• tie beam

Have you heard any other names for truss components. Let us all know in the comments below in case you have📝

As already mentioned, there is different types of the truss roof, meaning that the different elements can be built with different materials and systems.

One example of the truss roof type can be seen in the next picture, where a whole timber beams are chosen as top and bottom chords.

The top chords have a little overhang.

The webs/diagonals are connecting top and bottom chords, which leads to an “additional support” of those members because the span is reduced.  

For the wind bracing system can be used either wind bracing steel straps, wooden boards or another solution. This system is however not modelled and shown in the picture.

.. and here is the 3D model because they are an even better visualisation than 2D pictures, aren’t they?

We haven’t covered wind bracing systems yet, – how they work, why we need them – but would you be interested in learning more? Let me know in the comments below.

👆 Choose a Static system of the truss roof

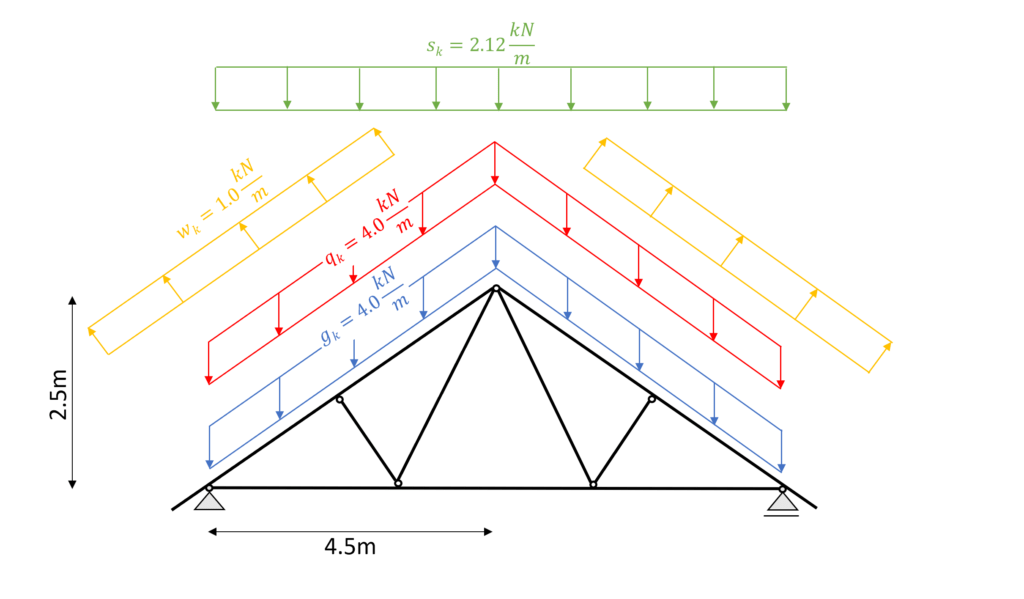
The static system of the truss roof is built up by 2 inclined timber beams and connected to each other at the top with a hinge.

Those beams are supported with a pinned and a roller support at its lowest point or – in case of a cantilevered overhang of the roof – close to the lowest point.

4 diagonals connect top and bottom chords with each other. Those diagonals or webs take up only normal forces and are therefore modelled as bar elements.

The static system of the truss roof is visualized in the next picture.

To not loose context – the 2D static system represents the following rafters. But it can also represent any other section of beams and bars. The spacing between the rafters is set to 4m.

The truss roof can of course also have different layouts with smaller/wider spans or steeper inclination.

⬇️ Characteristic Loads of the Truss roof

The loads will not be derived in this article. We explained the calculation of dead, live, wind and snow loads for pitched roofs thoroughly in previous articles.  

The defined load values are estimations from the previous calculations.

$g_{k}$	1.08 kN/m2	Characteristic value of dead load
$q_{k}$	1.0 kN/m2	Characteristic value of live load
$s_{k}$	0.53 kN/m2	Characteristic value of snow load

As we also discussed in the article about the characteristic snow load, there are 3 different load cases, where only half of the value is applied on one pitched side but the full value on the other.

However, due to simplicity we only consider load case 1 in this tutorial which applies $s_{k} = 0.53 kN/m^2$ on both rafters.

We split up the wind load from the above table due to the complexity of the wind with its wind areas and directions.

In this calculation, we will only focus on the external wind pressure for areas of 10 m2.

Wind direction front

$w_{k.F}$	-0.25(/0.35) kN/m2	Characteristic value of wind load Area F
$w_{k.G}$	-0.25(/0.35) kN/m2	Characteristic value of wind load Area G
$w_{k.H}$	-0.1(/0.2) kN/m2	Characteristic value of wind load Area H
$w_{k.I}$	-0.2(/0.0) kN/m2	Characteristic value of wind load Area I
$w_{k.J}$	-0.25(/0.0) kN/m2	Characteristic value of wind load Area J

Wind direction side

$w_{k.F}$	-0.55 kN/m2	Characteristic value of wind load Area F
$w_{k.G}$	-0.7 kN/m2	Characteristic value of wind load Area G
$w_{k.H}$	-0.4 kN/m2	Characteristic value of wind load Area H
$w_{k.I}$	-0.25 kN/m2	Characteristic value of wind load Area I

The following picture presents the static system of the truss roof with its line loads applied.

The section that is presented in Figure: Truss roof | 2D static system representing beams and bars is used for this example.

Due to simplicity, this tutorial looks only at the wind load from the side. Therefore, the wind load $w_{k.I} = -0.25 kN/m^2$ is applied to both rafters.

$g_{k}$	1.08 kN/m2 * 4.0m = 4.32 kN/m
$q_{k}$	1.0 kN/m2 * 4.0m = 4.0 kN/m
$s_{k}$	0.53 kN/m2 * 4.0m = 2.12 kN/m
$w_{k}$	-0.25 kN/m2 * 4.0m = -1.0 kN/m

➕ Load combinations of the Truss roof

Luckily we have already written an extensive article about what load combinations are and how we use them. In case you need to brush up on it you can read the blog post here.

We choose to include $w_{k.I.}$ = -0.25 kN/m2 as the wind load in the load combinations, as this is the wind load that is applied to the section we look at, and to keep the calculation clean.

In principle, you should consider all load cases.

However, with a bit more experience, you might be able to exclude some of the values.

In modern FE programs, multiple values for the wind load can be applied and load combinations automatically generated. So the computer is helping us a lot.

Just keep in mind that you should include all wind loads, but because of simplicity we do only consider 1 value in this article😁.

ULS Load combinations

I know you might not understand what that means when you do load combinations the first time, but we did a whole article about what loads exist and how to apply them on a pitched roof 😎.

LC1	$1.35 * 4.32 \frac{kN}{m} $
LC2	$1.35 * 4.32 \frac{kN}{m} + 1.5 * 4.0 \frac{kN}{m}$
LC3	$1.35 * 4.32 \frac{kN}{m} + 1.5 * 4.0 \frac{kN}{m} + 0.7 * 1.5 * 2.12 \frac{kN}{m}$
LC4	$1.35 * 4.32 \frac{kN}{m} + 0 * 1.5 * 4.0 \frac{kN}{m} + 1.5 * 2.12 \frac{kN}{m}$
LC5	$1.35 * 4.32 \frac{kN}{m} + 1.5 * 4.0 \frac{kN}{m} + 0.7 * 1.5 * 2.12 \frac{kN}{m} + 0.6 * 1.5 * (-1.0 \frac{kN}{m}) $
LC6	$1.35 * 4.32 \frac{kN}{m} + 0 * 1.5 * 4.0 \frac{kN}{m} + 1.5 * 2.12 \frac{kN}{m} + 0.6 * 1.5 * (-1.0 \frac{kN}{m}) $
LC7	$1.35 * 4.32 \frac{kN}{m} + 0 * 1.5 * 4.0 \frac{kN}{m} + 0.7 * 1.5 * 2.12 \frac{kN}{m} + 1.5 * (-1.0 \frac{kN}{m}) $
LC8	$1.35 * 4.32 \frac{kN}{m} + 1.5 * 2.12 \frac{kN}{m} $
LC9	$1.35 * 4.32 \frac{kN}{m} + 1.5 * (-1.0 \frac{kN}{m}) $
LC10	$1.35 * 4.32 \frac{kN}{m} + 1.5 * 4.0 \frac{kN}{m} + 0.6 * 1.5 * (-1.0 \frac{kN}{m}) $
LC11	$1.35 * 4.32 \frac{kN}{m} + 1.5 * (-1.0 \frac{kN}{m}) + 0.7 * 1.5 * 2.12 \frac{kN}{m} $
LC12	$1.35 * 4.32 \frac{kN}{m} + 1.5 * 2.12 \frac{kN}{m} + 0.6 * 1.5 * (-1.0 \frac{kN}{m})$

Characteristic SLS Load combinations

LC1	$4.32 \frac{kN}{m} $
LC2	$4.32 \frac{kN}{m} + 4.0 \frac{kN}{m}$
LC3	$4.32 \frac{kN}{m} + 4.0 \frac{kN}{m} + 0.7 * 2.12 \frac{kN}{m}$
LC4	$4.32 \frac{kN}{m} + 4.0 \frac{kN}{m} + 0.6 * (-1.0 \frac{kN}{m})$
LC5	$4.32 \frac{kN}{m} + 4.0 \frac{kN}{m} + 0.7 * 2.12 \frac{kN}{m} + 0.6 * (-1.0 \frac{kN}{m}) $
LC6	$4.32 \frac{kN}{m} + 0 * 4.0 \frac{kN}{m} + 2.12 \frac{kN}{m} + 0.6 * (-1.0 \frac{kN}{m}) $
LC7	$4.32 \frac{kN}{m} + 0 * 4.0 \frac{kN}{m} + 0.7 * 2.12 \frac{kN}{m} + (-1.0 \frac{kN}{m}) $
LC8	$4.32 \frac{kN}{m} + 2.12 \frac{kN}{m}$
LC9	$4.32 \frac{kN}{m} + (-1.0 \frac{kN}{m}) $
LC10	$4.32 \frac{kN}{m} + 4.0 \frac{kN}{m} + 0.6 * (-1.0 \frac{kN}{m}) $
LC11	$4.32 \frac{kN}{m} + (-1.0 \frac{kN}{m}) + 0.7 * 2.12 \frac{kN}{m} $
LC12	$4.32 \frac{kN}{m} + 0 * 4.0 \frac{kN}{m} + 2.12 \frac{kN}{m}$
LC13	$4.32 \frac{kN}{m} + 0 * 4.0 \frac{kN}{m} + (-1.0 \frac{kN}{m})$

👉 Define timber material properties

🪵 Truss timber material

For this blog post/tutorial we are choosing a Structural timber C24. More comments on which timber material to pick and where to get the properties from were made here.

The following characteristic strength and stiffness parameters were found online from a manufacturer.

Bending strength $f_{m.k}$	24 $\frac{N}{mm^2}$
Tension strength parallel to grain $f_{t.0.k}$	14 $\frac{N}{mm^2}$
Tension strength perpendicular to grain $f_{t.90.k}$	0.4 $\frac{N}{mm^2}$
Compression strength parallel to grain $f_{c.0.k}$	21 $\frac{N}{mm^2}$
Compression strength perpendicular to grain $f_{c.90.k}$	2.5 $\frac{N}{mm^2}$
Shear strength $f_{v.k}$	4.0 $\frac{N}{mm^2}$
E-modulus $E_{0.mean}$	11.0 $\frac{kN}{mm^2}$
E-modulus $E_{0.g.05}$	9.4 $\frac{kN}{mm^2}$

⌚ Modification factor $k_{mod}$

If you do not know what the modification factor $k_{mod}$ is, we wrote an explanation to it in a previous article, which you can check out.

Since we want to keep everything as short as possible, we are not going to repeat it in this article – we are only defining the values of $k_{mod}$.

For a residential house which is classified as Service class 1 according to EN 1995-1-1 2.3.1.3 we extract the following load durations for the different loads.

Self-weight/dead load	Permanent
Live load, Snow load	Medium-term
Wind load	Instantaneous

From EN 1995-1-1 Table 3.1 we get the $k_{mod}$ values for the load durations and a structural wood C24 (Solid timber).

			$k_{mod}$
Self-weight/dead load	Permanent action	Service class 1	0.6
Live load, Snow load	Medium term action	Service class 1	0.8
Wind load	Instantaneous action	Service class 1	1.1

🦺 Partial factor for material properties $\gamma_{M}$

According to EN 1995-1-1 Table 2.3 the partial factor $\gamma_{M}$ is defined as

$\gamma_{M} = 1.3$

📏 Assumption of width and height of truss beams and diagonals

We are defining the width w and height h of the C24 structural wood beam top chord Cross-section as

Width w = 120 mm
Height h = 220 mm

.. the values for the compression diagonal are defined as

Width w = 60 mm
Height h = 120 mm

.. the cross-sectional dimensions of the tension diagonal are defined as

Width w = 60 mm
Height h = 100 mm

.. and lastly the dimensions of the tension bottom chord are

Width w = 100 mm
Height h = 160 mm

💡 We highly recommend doing any calculation in a program where you can always update values and not by hand on a piece of paper! I made that mistake in my bachelor.

In any course and even in my bachelor thesis, I calculated everything except the forces (FE program) on a piece of paper.

Now that we know the width and the height of the top chord Cross-section, we can calculate the Moment of inertias $I_{y}$ and $I_{z}$.

$I_{y} = \frac{w \cdot h^3}{12} = \frac{120mm \cdot (220mm)^3}{12} = 1.065 \cdot 10^8 mm^4 $

$I_{z} = \frac{w^3 \cdot h}{12} = \frac{(120mm)^3 \cdot 220mm}{12} = 3.17 \cdot 10^7 mm^4 $

.. for the compression diagonal

$I_{y} = \frac{w \cdot h^3}{12} = \frac{60mm \cdot (120mm)^3}{12} = 8.64 \cdot 10^6 mm^4 $

$I_{z} = \frac{w^3 \cdot h}{12} = \frac{(60mm)^3 \cdot 120mm}{12} = 2.16 \cdot 10^6 mm^4 $

.. and for the bottom chord

$I_{y} = \frac{w \cdot h^3}{12} = \frac{100mm \cdot (160mm)^3}{12} = 3.413 \cdot 10^7 mm^4 $

$I_{z} = \frac{w^3 \cdot h}{12} = \frac{(100mm)^3 \cdot 160mm}{12} = 1.33 \cdot 10^7 mm^4 $

🆗 ULS Design

In the ULS (ultimate limit state) Design we verify the stresses in the timber members due to bending, shear and normal forces.

In order to calculate the stresses of the rafters, we need to calculate the Bending Moments, Normal and Shear forces due to different loads. An FE or beam program is used to execute this task.

🧮 Calculation of bending moment, normal and shear forces

We use a FE programm to calculate the bending moments, normal and shear forces. Load combination 3 with live load as leading and snow load as reduced load leads to the highest results which we visualize.

Load combination 3

Load combination 3 – Bending moments

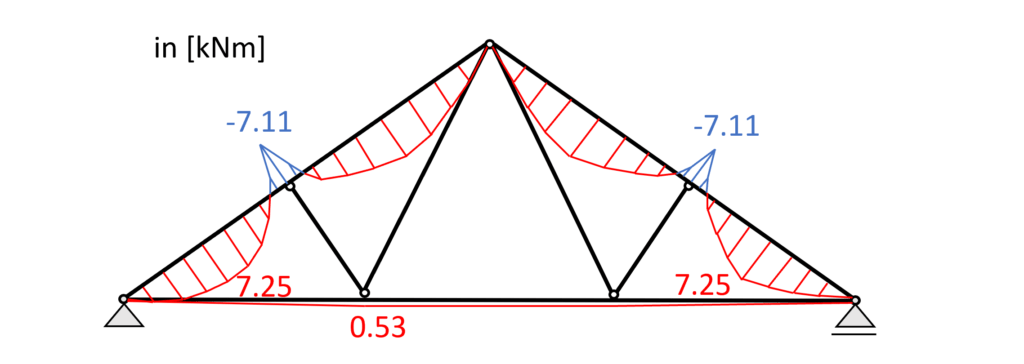
Does the moment distribution of the top chords remind you of something…?🤔

Maybe the one from a continuous beam?😀

Load combination 3 – Shear forces

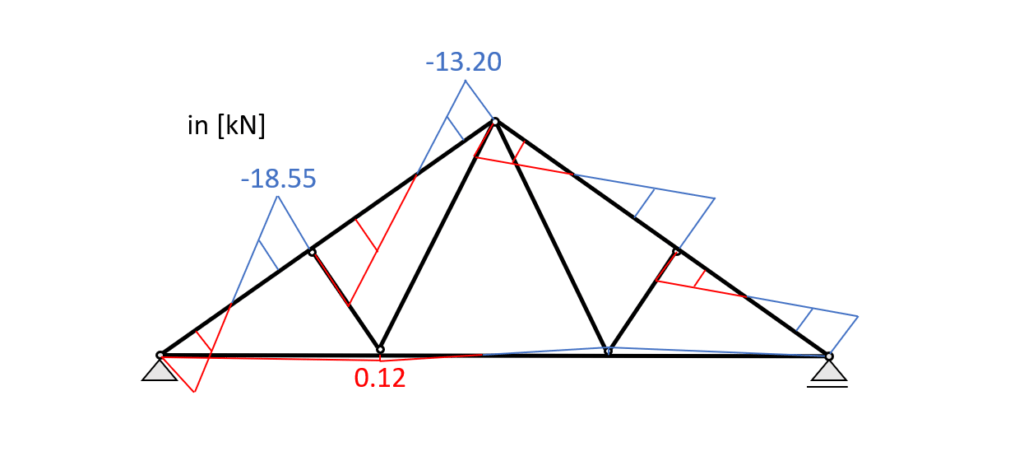
Load combination 3 – Normal forces

🔎 Bending and Compression Verification

Top chords

From the max. bending moment in the span (7.25 kNm) and the compression force (117.2kN) in the same point we can calculate the stress in the most critical cross section.

Bending stress:

$\sigma_{m} = \frac{M_{d}}{I_{y}} \cdot \frac{h}{2} = \frac{7.25 kNm}{1.065 \cdot 10^{-4}} \cdot \frac{0.22m}{2} = 7.49 MPa$

Compression stress:

$\sigma_{c} = \frac{N_{d}}{w \cdot h} = \frac{117.2 kN}{0.12m \cdot 0.22m} = 4.44 MPa$

Resistance stresses of the timber material:

$ f_{d} = k_{mod} \cdot \frac{f_{k}}{\gamma_{m}} $

LC3 (M-action)	$k_{mod.M} \cdot \frac{f_{m.k}}{\gamma_{m}} $	$0.8 \cdot \frac{24 MPa}{1.3} $	$14.77 MPa $
LC3 (M-action)	$k_{mod.M} \cdot \frac{f_{c.k}}{\gamma_{m}} $	$0.8 \cdot \frac{21 MPa}{1.3} $	$12.92 MPa $

Utilization according to EN 1995-1-1 (6.19)

$\eta = (\frac{\sigma_{c}}{f_{c.d}})^2 +  \frac{\sigma_{m}}{f_{m.d}} = 0.625 < 1.0$

Diagonal – Compression only

Now let’s do the same for the compression diagonal/web, and let’s remember that we modelled the elements as bars.

We have therefore only Normal forces. From the max. compression force (37.04kN) in the diagonal, we can calculate the most critical stress.

Compression stress:

$\sigma_{c} = \frac{N_{d}}{w \cdot h} = \frac{37.04 kN}{0.06m \cdot 0.12m} = 5.14 MPa$

Utilization according to EN 1995-1-1 (6.19)

$\eta = \frac{\sigma_{c}}{f_{c.d}} = 0.4 < 1.0$

👍 Shear Verification – Top chords

From the max. shear force (midsupport: 18.55 kN) we can calculate the shear stress in the most critical cross section.

Shear stress:

$\tau_{d} = \frac{3V}{2 \cdot w \cdot h} =  \frac{3 \cdot 18.55 kN}{2 \cdot 0.12m \cdot 0.22m} = 1.05 MPa$

Resistance stresses of the timber material:

$ f_{v} = k_{mod.M} \cdot \frac{f_{v}}{\gamma_{m}} $

$ f_{v} = 0.8 \cdot \frac{4 MPa}{1.3} = 2.46 MPa$

Utilization according to EN 1995-1-1 (6.13)

$\eta = \frac{\tau_{v}}{f_{v}} = 0.43 < 1.0$

👨‍🏫Buckling Verification

Top chords

We assume that buckling out of the plane (z-direction) can be neglected because the rafters are held on the sides. Therefore we can define the buckling length $l_{y}$ as

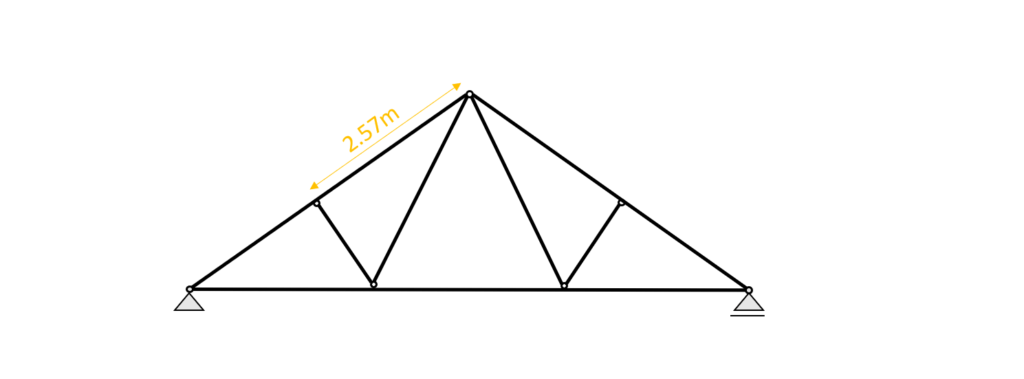
$l_{y} = 2.57m$

Radius of inertia

$i_{y} = \sqrt{\frac{I_{y}}{w \cdot h}} = 0.064m$

Slenderness ratio

$\lambda_{y} = \frac{l_{y}}{i_{y}} = 40.47$

Relative slenderness ratio (EN 1995-1-1 (6.21))

$ \lambda_{rel.y} = \frac{\lambda_{y}}{\pi} \cdot \sqrt{\frac{f_{c.0.k}}{E_{0.g.05}}}  = 0.61$

$\beta_{c}$ factor for solid timber (EN 1995-1-1 (6.29))

$\beta_{c} = 0.2$

Instability factor (EN 1995-1-1 (6.27))

$k_{y} = 0.5 \cdot (1+ \beta_{c} \cdot (\lambda_{rel.y} – 0.3) + \lambda_{rel.y}^2) = 0.72$

Buckling reduction coefficient (EN 1995-1-1  (6.25))

$k_{c.y} = \frac{1}{k_{y} + \sqrt{k_{y}^2 – \lambda_{rel.y}^2}} = 0.915$

Utilization (EN 1995-1-1 (6.23))

$\frac{\sigma_{c}}{k_{c.y} \cdot f_{c.d}} + \frac{\sigma_{m}}{f_{m.d}} = 0.88 < 1$

Diagonal – Compression only

Buckling out of plane is assumed to have the same buckling length as in plane. Therefore we can define the buckling lengths $l_{y}$ and $l_{z}$ as

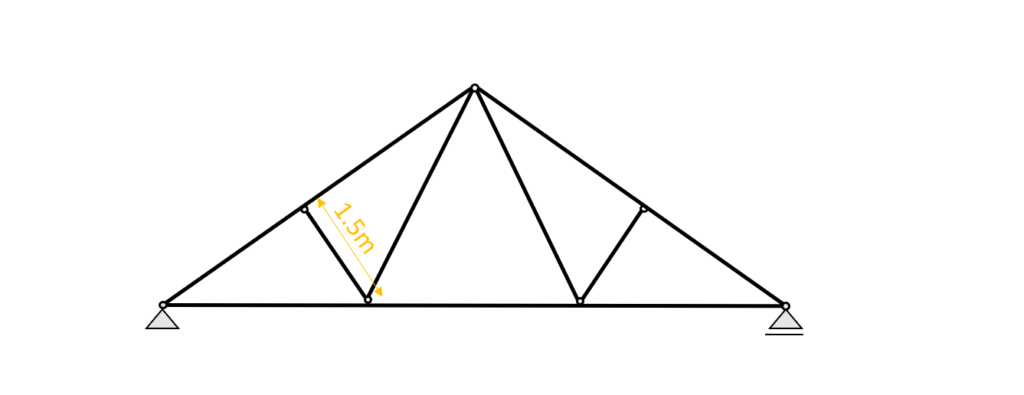
$l_{y} = 1.5m$

$l_{z} = 1.5m$

Radius of inertia

$i_{y} = \sqrt{\frac{I_{y}}{w \cdot h}} = 0.035m$

$i_{z} = \sqrt{\frac{I_{z}}{w \cdot h}} = 0.017m$

Slenderness ratio

$\lambda_{y} = \frac{l_{y}}{i_{y}} = 43.3$

$\lambda_{z} = \frac{l_{z}}{i_{z}} = 86.6$

Relative slenderness ratio (EN 1995-1-1 (6.21))

$ \lambda_{rel.y} = \frac{\lambda_{y}}{\pi} \cdot \sqrt{\frac{f_{c.0.k}}{E_{0.g.05}}}  = 0.651$

$ \lambda_{rel.z} = \frac{\lambda_{z}}{\pi} \cdot \sqrt{\frac{f_{c.0.k}}{E_{0.g.05}}}  = 1.303$

$\beta_{c}$ factor for solid timber (EN 1995-1-1 (6.29))

$\beta_{c} = 0.2$

Instability factor (EN 1995-1-1 (6.27))

$k_{y} = 0.5 \cdot (1+ \beta_{c} \cdot (\lambda_{rel.y} – 0.3) + \lambda_{rel.y}^2) = 0.747$

$k_{z} = 0.5 \cdot (1+ \beta_{c} \cdot (\lambda_{rel.z} – 0.3) + \lambda_{rel.z}^2) = 1.449$

Buckling reduction coefficient (EN 1995-1-1  (6.25))

$k_{c.y} = \frac{1}{k_{y} + \sqrt{k_{y}^2 – \lambda_{rel.y}^2}} = 0.898$

$k_{c.z} = \frac{1}{k_{z} + \sqrt{k_{z}^2 – \lambda_{rel.z}^2}} = 0.48$

Utilization (EN 1995-1-1 (6.23))

$\frac{\sigma_{c}}{k_{c.y} \cdot f_{c.d}}= 0.443$

$\frac{\sigma_{c}}{k_{c.z} \cdot f_{c.d}}= 0.828$

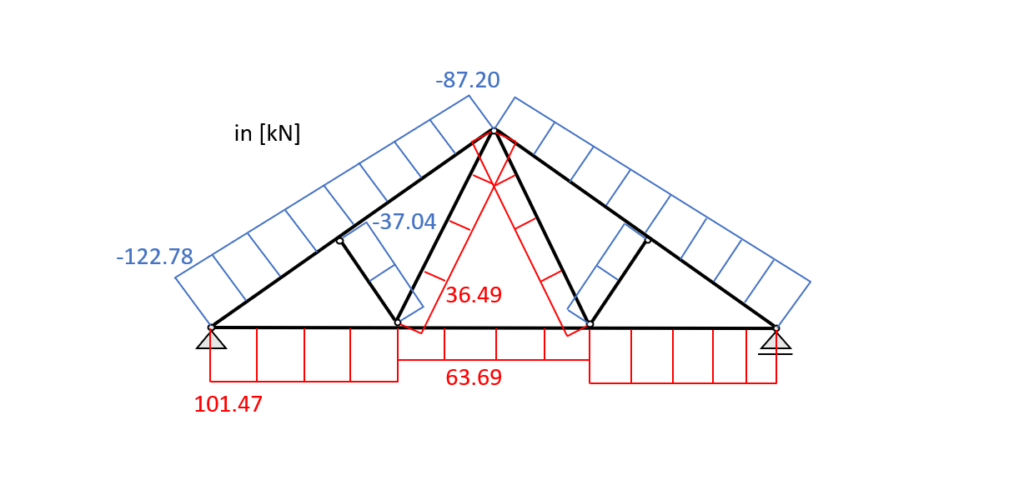
📋Bending and Tension Verification

Bottom chord

From the max. bending moment in the bottom chord beam (0.53 kNm) and the tension force (101.47 kN) in the same point we can calculate the stress in the most critical cross section.

Bending stress:

$\sigma_{m} = \frac{M_{d}}{I_{y}} \cdot \frac{h}{2} = \frac{0.53 kNm}{3.41 \cdot 10^{-5}} \cdot \frac{0.16m}{2} = 1.24 MPa$

Tension stress:

$\sigma_{t} = \frac{N_{d}}{w \cdot h} = \frac{101.47 kN}{0.1m \cdot 0.16m} = 6.34 MPa$

Resistance stresses of the timber material:

$ f_{d} = k_{mod} \cdot \frac{f_{k}}{\gamma_{m}} $

LC3 (M-action)

$k_{mod.M} \cdot \frac{f_{t.k}}{\gamma_{m}} $

$0.8 \cdot \frac{14 MPa}{1.3} $

$8.62 MPa $

Utilization according to EN 1995-1-1 (6.17)

$\eta = \frac{\sigma_{t}}{f_{t.d}} +  \frac{\sigma_{m}}{f_{m.d}} = 0.82 < 1.0$

Diagonal – Tension only

The maximum tension force in the diagonals is 36.5 kN

Tension stress:

$\sigma_{t} = \frac{N_{d}}{w \cdot h} = \frac{36.5 kN}{0.06m \cdot 0.1m} = 6.05 MPa$

Utilization according to EN 1995-1-1 (6.17)

$\eta = \frac{\sigma_{t}}{f_{c.d}} = 0.7 < 1.0$

👩‍🏫 SLS Design – Truss roof

We also discussed the SLS design a bit more in detail in a previous article. In this blog post we are not explaining too much but rather show the calculations😊

🖋️Instantaneous deformation $u_{inst}$

$u_{inst}$ (instantaneous deformation) of our beam can be calculated with the load of the characteristic load combination.

As for the bending moments, shear and axial forces we are using a FE program to calculate the deflections due to our Load combinations.

LC 3 of the characteristic SLS load combinations leads to the largest deflection u.

$u_{inst}$ = 9.2 mm

Unfortunately EN 1995-1-1 Table 7.2 recommends values for $w_{inst}$ only for “Beams on two supports” and “Cantilevering beams” and not for a truss system like in this case.

However, the limits of the deflection can be agreed upon with the client and the structure is not collapsing due to too large deflections if the rafter is verified for all ULS calculations.

The moment and shear distribution of the top chord are similar to a continuous beam, but because the “middle support” is a compression member which is translating downwards because it’s connected to the bottom chord which deflects downwards, the limits for a simply supported beam for the whole top chord length is assumed in this tutorial (EN 1995-1-1 Table 7.2).

❓But my question to you: What limit would you use in this case? Let me know in the comments below.

$w_{inst}$ = l/300 = 5.15m/300 = 17.17 mm

Utilization

$\eta = \frac{u_{inst}}{w_{inst}} =  \frac{9.2mm}{17.17mm} = 0.536 < 1$

🏇Final deformation $u_{fin}$

$u_{fin}$ (final deformation) of our beam/rafter can be calculated by adding the creep deformation $u_{creep}$ to the instantaneous deflection $u_{inst}$.

Therefore, we will calculate the creep deflection with a FE program.

This might be a bit quick, but we have already covered the basics in the article about the timber beam dimensioning.

So check that out if you want to know exactly how to calculate $u_{creep}$ by hand. Let me know in the comments below if you struggle with calculating the creep deformation.

The creep deformation of LC3 is calculated as

$u_{creep}$ = 2.64mm

Adding the creep to the instantaneous deflection leads to the final deflection.

$u_{fin} = u_{inst} + u_{creep} = 9.2mm + 2.64mm= 11.84mm$

Limit of $u_{fin}$ according to EN 1995-1-1 Table 7.2

$w_{fin}$ = l/150 = 5.15m/150 = 34.3 mm

Utilization

$\eta = \frac{u_{fin}}{w_{fin}} =  \frac{11.84mm}{34.3mm} = 0.35$

Now that the truss is verified for compression, bending, buckling, tension and deflection we can finally say that the cross-section heights and widths are verified – check✔️.

After designing rafter, purlin, collar beam roof, it’s very interesting to see the difference in cross-sectional areas for each of the roof, right?

I am curious to hear from you: Which is your favourite roof system? Which truss layout have you already used in a design? Let me know in the comments✍️.

❓ Timber Truss Roof FAQ