Warren Truss: What is it? And How to Calculate it?

Warren Trusses are commonly used in railway bridges.

But why is that? Why is in some designs the Warren Truss favoured over the Pratt or Howe Truss?

To get an answer to those questions, we need to understand the structural system and how the loads travel through its different members.

So in this post, we’ll show what the Warren Truss is, its static system(s), which members act in compression or tension and how to calculate the internal forces.

Without further ado. Let’s talk WARREN TRUSSES. 🚀🚀

What Is the Warren Truss?

The Warren truss is a structural system which can carry loads with relatively long spans compared to beams. It was patented by engineers James Warren and Willoughby Monzoni in 1946.

The Warren truss is characterized by having tension and compression members, which we’ll calculate later in this article.

Let’s have a look at the Warren Truss and its different members. In the picture, you can see the names of the members of a Warren Truss.

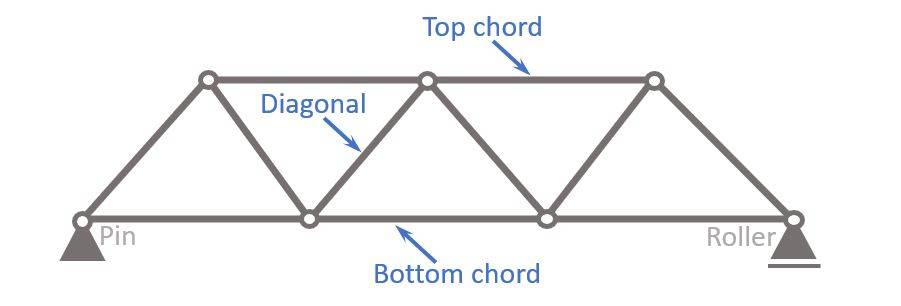
• Top chord
• Bottom chord
• Diagonals (sometimes called strut or tie depending on compression or tensions)

What is the Warren Truss used for?

The main application where Warren Trusses are used are Bridge Structures.

In most cases, steel is the main material for Warren trusses, however timber and concrete can also be an option.

A mix of different elements is also an option. For example, the diagonals and top chord can be built in steel, while the bottom chord is integrated into the deck and built in concrete.

Let’s look at the static system to get a better understanding of the structural behaviour of the Warren Truss.🚀🚀

Static System

Most truss structures are designed with hinge connections, mainly due to 2 reasons:

• Easier to calculate: Trusses with hinge connections make the structure statically determinate, which means that the internal forces can be calculated by hand. Especially until advanced Finite element software programs weren’t widely available, this was the main reason for using hinge connections. If fixed connections are used, but no software is available, advanced methods like the method of consistent deformation can be used. However, these methods are complicated and susceptible to calculation failures.
• Cost: Hinge connections are cheaper to build than fixed connections.

It definitely makes sense to be aware of the differences of a truss with hinges and fixed connections. In the picture below, you can see the “normal” Warren truss with hinge connections.

We summarize the characteristics of the truss with fixed connections a bit further below.

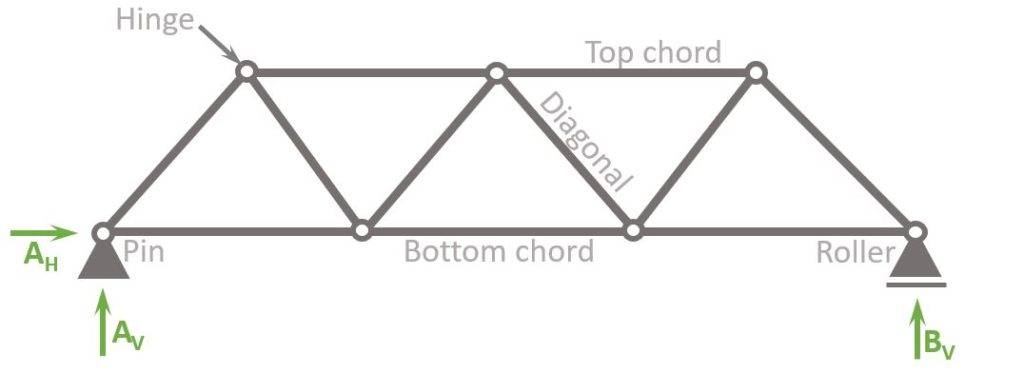
The static system of the Warren truss is characterized by having

• hinge connections at all nodes
• a pin and roller support, which makes the system statically determinate. Therefore, the internal forces can be calculated with the 3 equilibrium equations.

Warren Truss with fixed connections

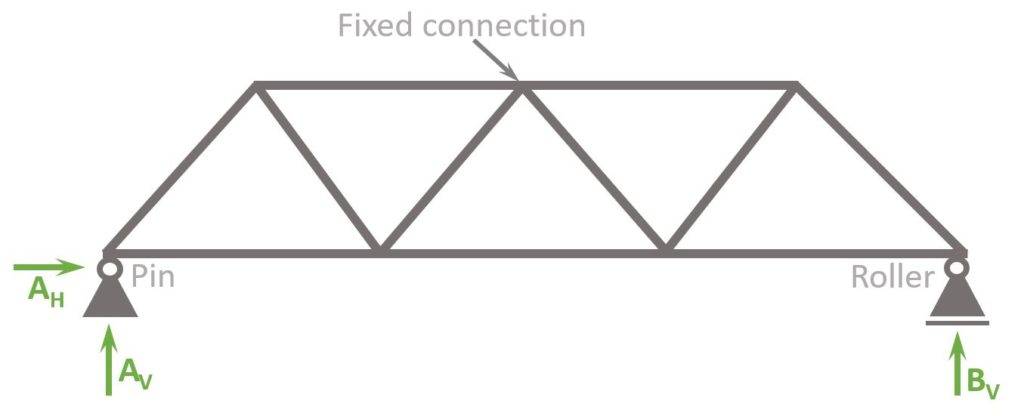
The Warren truss with fixed connections has the following differences to hinge connections:

• Bending moments in the connections
• More rigidity -> more robustness
• Smaller vertical deflection

Alright, now that we have learned how to set up our static system, we are ready to calculate the internal compression and tension forces of the truss.🎉🎉

Warren Truss Analysis

Let’s say our Warren Truss is a bridge structure. Therefore, the truss is exposed to dead and traffic load mainly on the bridge deck, which transfers the loads to the bottom chord.

We also simplify and say that the design load (Load combination of dead and traffic load) is 200 kN/m.

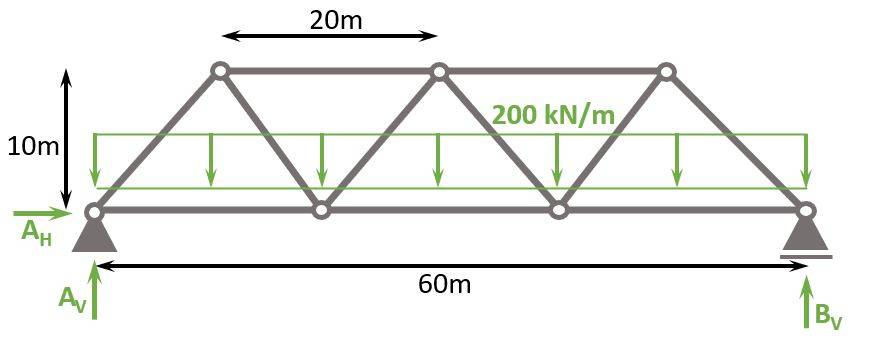
To calculate the compression and tension forces of the truss members with the 3 equlibrium equations, we do another approximation.

The Line load of 200 kN/m is approximated as point loads in the nodes, because otherwise the bottom chord members would be beams, which makes the calculation a lot more difficult.

The point load applied to nodes (a) and (d) is calculated as

$$200 kN/m \cdot 10m = 2000 kN$$

while the point loads applied to nodes (b) and (c) is calculated as

$$200 kN/m \cdot 20m = 4000 kN$$

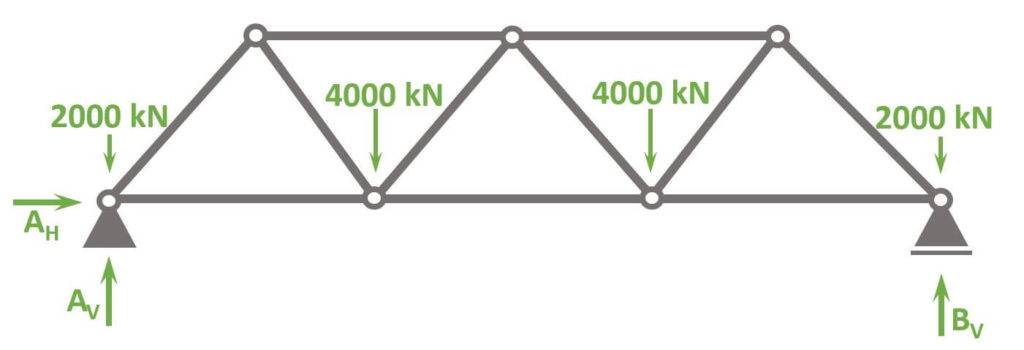
Before we start with the calculations, let’s give the nodes 🔵 and bars 🔴 some indices, so the identification is easier later in the internal force calculation.

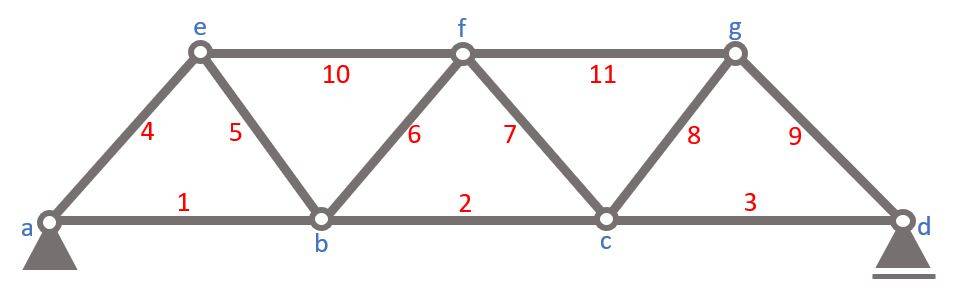
Let’s calculate. 🚀🚀

Calculation of Reaction Forces

As the structure is statically determinate, the reaction forces can be calculated with the 3 Equilibrium equations.

In our case, we are calculating the support forces A_H, A_V and B_V.

$\sum H = 0: A_H = 0$

$\sum V = 0: A_V + B_V \, – 2 \cdot 2000 \, \mbox{kN} – 2 \cdot 4000 \, \mbox{kN} = 0 $ -> $V_a = V_b = \frac{12000}{2} \mbox{kN} = 6000 \mbox{kN}$

$\sum M = 0: M_a = 0$

Calculation of the internal forces

Node a

Alright, now that we know the reaction forces, we can calculate the normal force of the first bar elements 1 and 4.

To do that, we only look at node 1 and its point loads/normal forces A_V, 2000 kN, N₁ and N₄.

$$ \alpha = 45 ° $$

Vertical Equilibrium:

$$ \sum V = 0: A_v – 2000 kN + N_4 \cdot sin(\alpha) = 0$$

Let’s solve that for N₄.

$$ N_4 = \frac{2000 kN – 6000 kN}{sin(\alpha)} = -5656.85 kN$$

Horizontal Equilibrium:

$$ \sum H = 0: N_4 \cdot cos(\alpha) + N_1 = 0$$

Let’s solve that for N₁.

$$ N_1 = – N_4 \cdot cos(\alpha) = 4000 kN$$

Node e

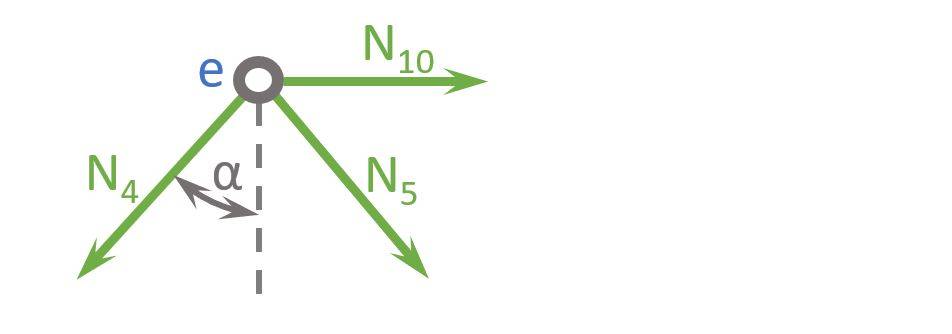
$$ \alpha = 45 ° $$

Vertical Equilibrium:

$$ \sum V = 0: N_4 \cdot cos(\alpha) + N_5 \cdot cos(\alpha) = 0$$

Let’s solve that for N₅.

$$ N_5 = – N_4 = 5656.85 kN$$

Horizontal Equilibrium:

$$ \sum H = 0: -N_4 \cdot sin(\alpha) + N_5 \cdot sin(\alpha) + N_{10} = 0$$

Let’s solve that for N₁₀.

$$ N_{10} = N_4 \cdot sin(\alpha) – N_5 \cdot sin(\alpha) = -8000 kN$$

Node b

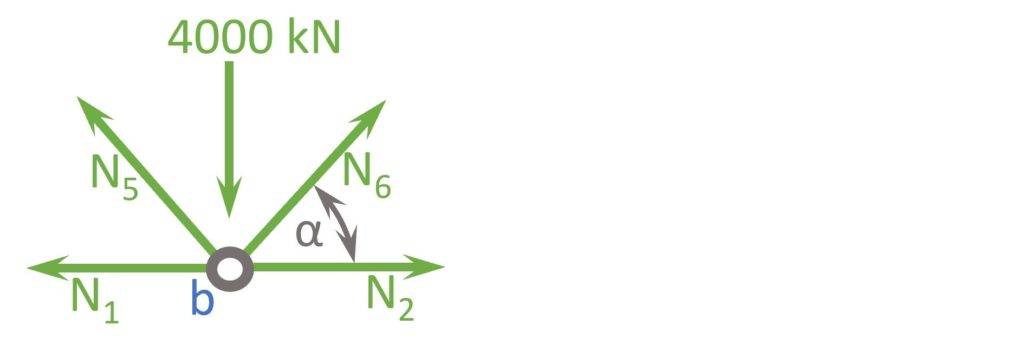
$$ \alpha = 45 ° $$

Vertical Equilibrium:

$$ \sum V = 0: N_5 \cdot sin(\alpha) + N_6 \cdot sin(\alpha) – 4000 kN= 0$$

Let’s solve that for N₆.

$$ N_6 = – N_5 + \frac{4000 kN}{sin(\alpha}= 0$$

Horizontal Equilibrium:

$$ \sum H = 0: -N_1 + N_2 – N_5 \cdot cos(\alpha) = 0$$

Let’s solve that for N₂.

$$ N_{2} = N_1 + N_5 \cdot cos(\alpha) = 8000 kN$$

Well done! Now we have calculated the normal forces of ALL bars.

What all? But we are missing half of the bars?

Yes! But due to symmetry we know that N₁ = N₃, N₄ = N₉, N₅ = N₈, N₆ = N₇, N₁₀ = N₁₁.

So, to summarize it, a normal force diagram helps to understand how the loads travel through the truss.

Normal force diagram

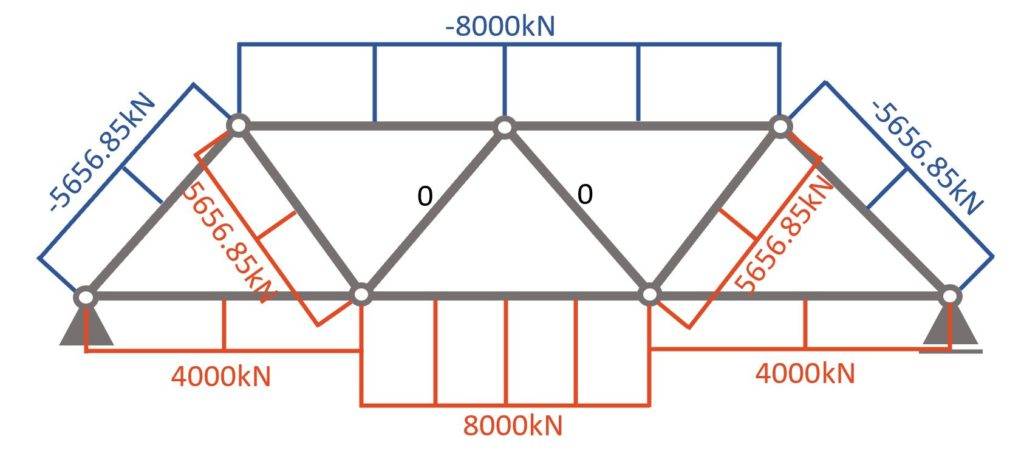
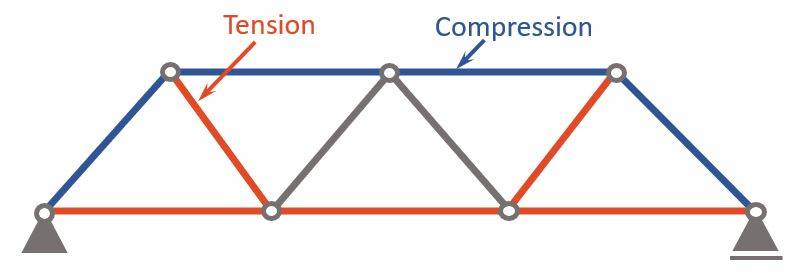
Compression and Tension Members

Now, as you can see in the normal force diagram, some members have a positive (+) and some have a negative (-) normal force.

A negative (-) normal force means that the member is under compression 🔵, while a positive (+) normal force means that the member acts in tension 🔴.

Advantages and Disadvantages

Pros

• Cost-effective due to their efficient design
• Widely accepted around the world
• Easy to construct
• Very stable structure: Good buckling resistance as compression members are not too long

Cons

• Warren Truss doesn’t spread concentrated loads such as point loads evenly to all members. Most of the load is taken by the closest members. If this is considered in the design, the cross-section of the members taking up the concentrated load increases.
• Big deflection for long spans

Conclusion

Now, that you got an overview of the Warren Truss, and how we calculate its internal forces, you can learn about loads, because every truss is exposed to loads.

1. Snow load on a flat roof
2. Wind load on a flat roof
3. Wind load on walls

Because there are always multiple loads acting on Warren Trusses, considering these different loads in the structural design is done by setting up Load Combinations with safety factors.🦺

Once all load cases and combinations are set up, the structural elements can be designed. We have already written a guide on how to design a timber truss. Check it out!

• Timber truss roof design

I hope that this article helped you understand the Warren Truss and how to go further from here. In case you still have questions.

Let us know in the comments below ✍️.

Warren Truss FAQ