What Is a Beam? And 7 Types of Beams
Have you heard somebody mentioning the word beam a few times but didn’t really know what it is? 🤔🤔
Well, experts such as structural engineers or teachers often assume that everyone knows what a beam is, as we humans are surrounded by beams every day.
But it’s a very technical term, and beams have certain characteristics that only engineers are aware of.
So what’s a beam? 🙋♂️🙋♂️
Short answer: A horizontal element carrying floors and other loads such as people. Beams are material independent. So timber, concrete and steel are common materials of beams.
But there’s much more to it.
Stick for the long answer and learn about the 7 different types of beams that are used in structural engineering.
Or in case you enjoy videos more than text, then check out our YouTube video. 📺📺
So, let’s get into it.
What Is a Beam?
Beams are horizontal elements which carry loads mostly perpendicular to its axis to distribute them to its supports. One characteristic of beams is that they act in bending, which occurs when loads act perpendicular to the element axis.
In most cases, beams take up vertical loads such as dead and live loads of floors in buildings and distribute them to columns or walls.
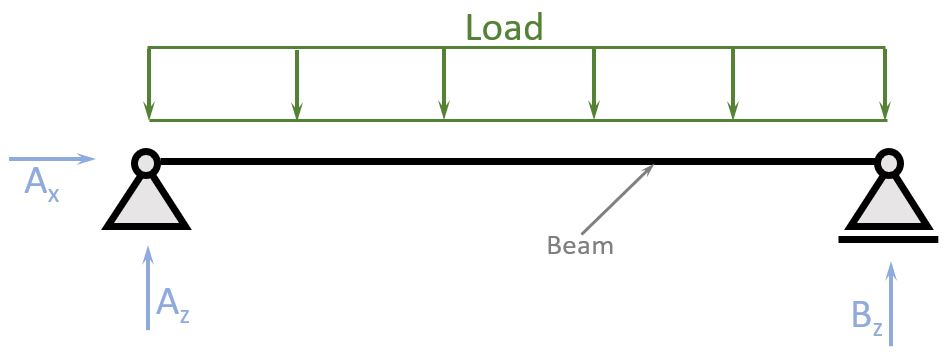
Supports basically determine the type of beam. So let’s have a quick look at the different types of supports.
- Pin
- Roller
- Fixed support
- Spring
Real-world examples of beams are
- Timber roof rafters🪵
- Concrete/steel beams in parking garages supporting the deck🚗
- Timber purlins
- Horizontal elements of a steel framing
- Concrete deck of a suspension bridge
- And many more.
Let’s have a closer look at the types of static systems of beams that we use in structural engineering.
Types of Beams
The following 7 types of beams are the most common static systems of beams used in structural engineering.
We attached real-world examples to those static systems.
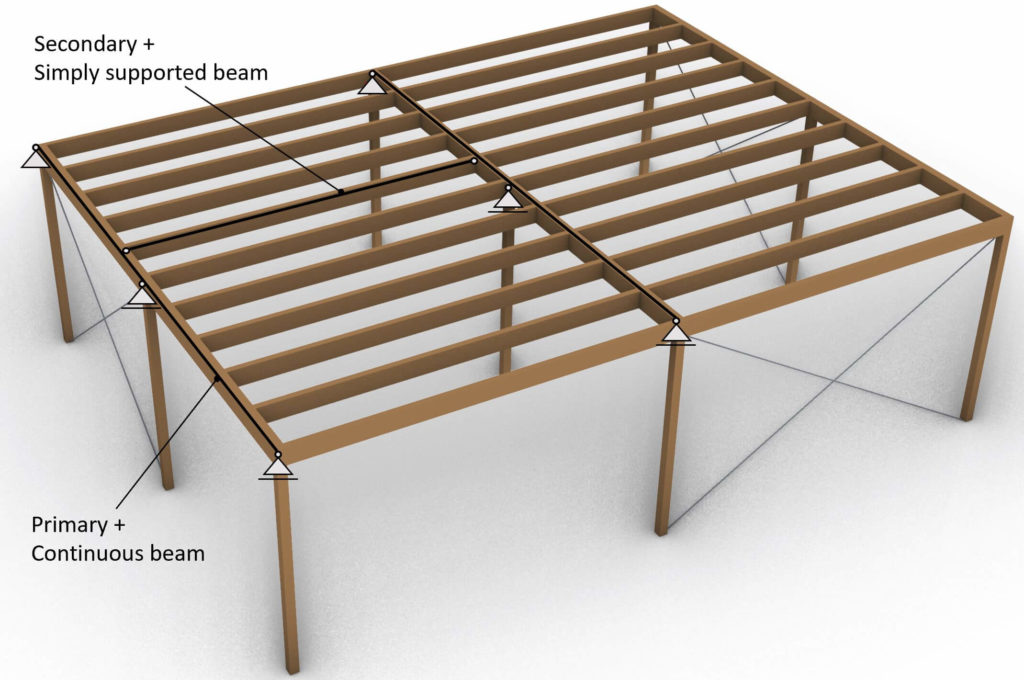
Simply Supported Beam
Static System
Simply supported beams are the most used static system. It’s usually the first static system that is introduced in university, for a good reason. Calculating the internal and reaction forces due to loads is very easy because the static system is statically determinate. This means that all forces can be calculated by hand with the 3 equilibrium equations.
Supports
1 Pin, 1 Roller
Reactions
Pin = Horizontal Ax + Vertical Az, Roller = Vertical Bz
Examples
Timber beam
Steel beam
Timber flat roof
Hand calculation of internal forces of a simply supported beam
Cantilever Beam
Static System
Cantilever beams are, after simply supported beams, the 2nd most used static system in structural engineering. There are plenty of cantilever beams in our daily lives, such as balconies, cranes or high-rise buildings. Calculating the internal and reaction forces due to loads is very easy because the static system is statically determinate. This means that all forces can be calculated by hand with the 3 equilibrium equations.
Supports
1 Fixed support
Reactions
Fixed support = Horizontal Ax + Vertical Az, Moment MA
Examples
Hand calculation of internal forces of a cantilever beam
2-Span Continuous Beam
Static System
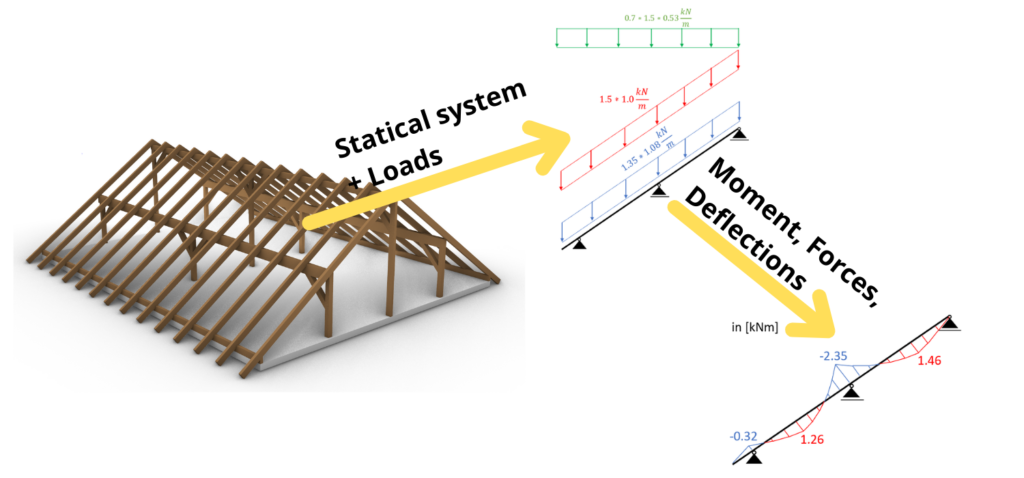
2-span continuous beams are not as common any more as simply supported or cantilever beams. This static system is characterized by its 3 supports – 2 on the ends and one in between. Calculating the internal and reaction forces can also not be done easily with the equilibrium equations. Either formulas or FEM programs are used to calculate the forces. An example of a 2-span continuous beam is a rafter of a roof which is supported by 3 purlins.
Supports
1 Pin, 2 Roller
Reactions
Pin = Horizontal Ax + Vertical Az, Roller = Vertical Bz
Example
Design of rafter supported by 3 purlins
3-Span Continuous Beam
Static System
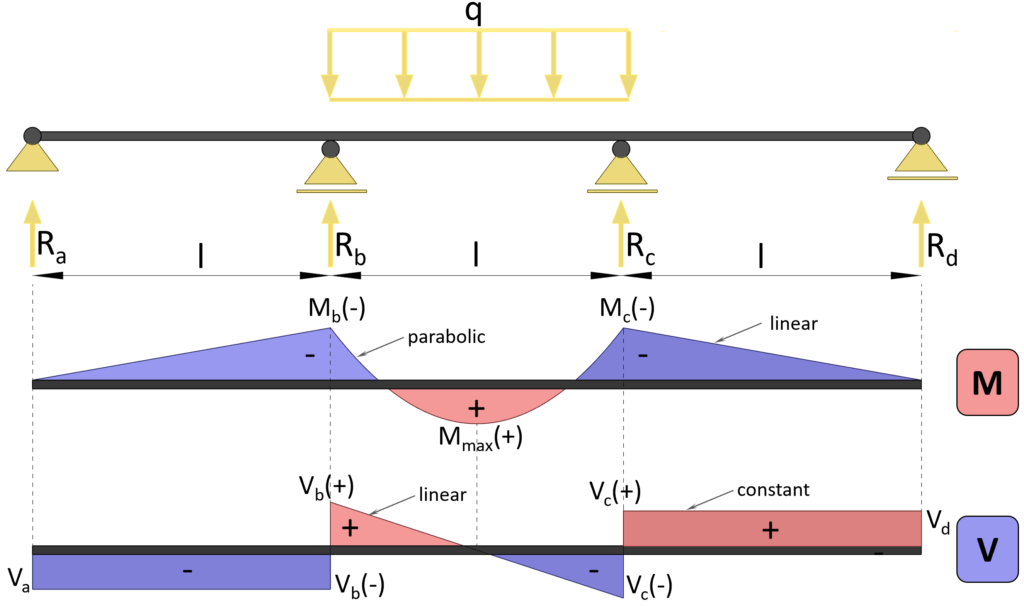
The 3-span continuous beam is characterized by its 4 supports – 2 on the ends and 2 in between. Calculating the internal and reaction forces can also not be done easily with the equilibrium equations. Either formulas or FEM programs are used to calculate the forces.
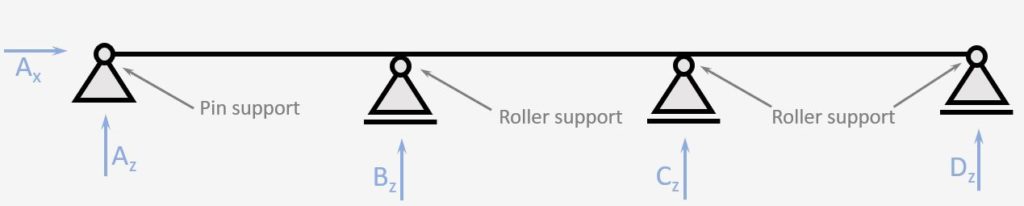
Supports
1 Pin, 3 Roller
Reactions
Pin = Horizontal Ax + Vertical Az, Roller = Vertical Bz
Example
Formula cheat sheet of internal forces of a 3-span continuous beam
X-Span Continuous Beam
Static System
Now, a beam can have as many continuous supports as required. The x in x-span continuous beam stand for a number. This static system has 1 pin and x-1 roller supports. Calculating the internal and reaction forces can also not be done easily with the equilibrium equations. Either formulas or FEM programs are used to calculate the forces. An example of an x-span continuous beam is a very first approximation of the deck of a cable stayed bridge.
Supports
1 Pin, X Roller
Reactions
Pin = Horizontal Ax + Vertical Az, Roller = Vertical Bz
Example
Static system of 2D cable stayed bridge
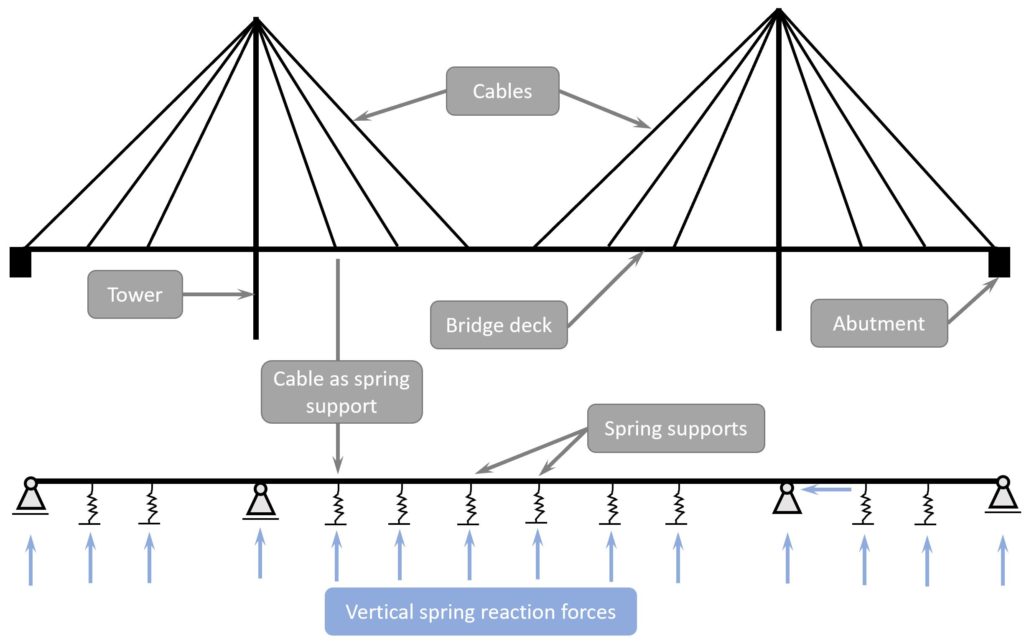
Please note, that in an even earlier approximation the spring supports are modelled as rollers. Based on the vertical reaction forces of those rollers, the spring stiffness is calculated.
Fixed Beam
Static System
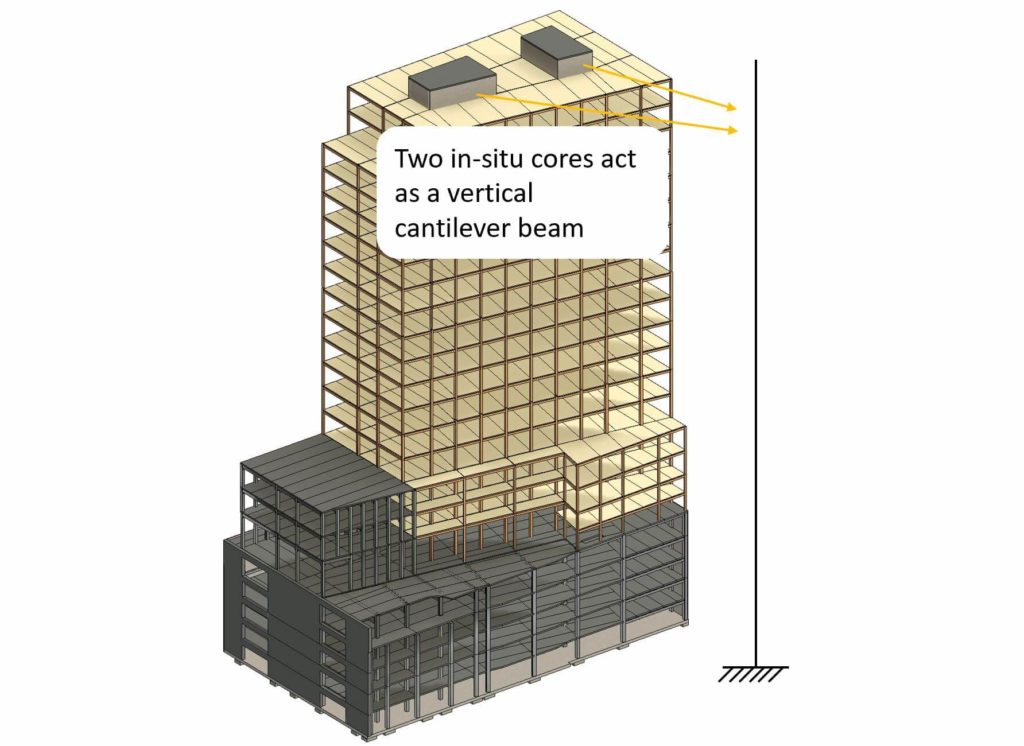
A beam with 2 fixed supports is a rarely used static system. One use case is when 2 concrete cores of a high-rise building need to be connected to make the building more rigid. These beams could be designed with concrete or steel beams. Calculating the internal and reaction forces can also not be done easily with the equilibrium equations. Either formulas or FEM programs are used to calculate the forces, as this static system is statically indeterminate.
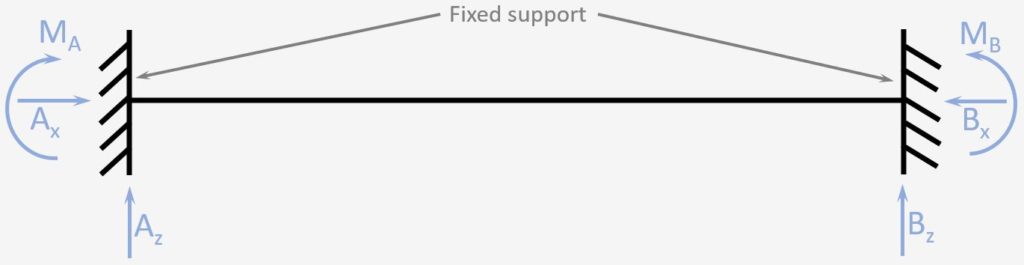
Supports
1 Pin, 2 Roller
Reactions
Fixed support = Horizontal Ax + Vertical Az, Moment MA
Beam with Roller & Fixed Support
Static System
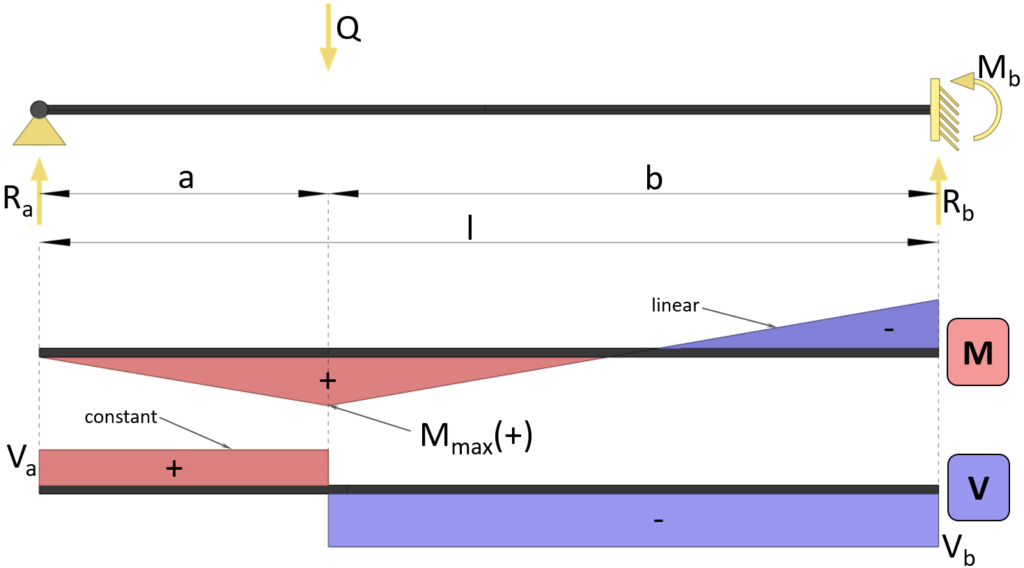
A beam with roller and fixed support is rarely used. Use cases of this static system are for example an in-situ concrete beam supported on one side by an in-situ concrete core/wall and on the other side by a concrete column. The designer could choose the fixed connection so that the structure is more rigid and robust.
Supports
1 Fixed Support, 1 Roller
Reactions
Fixed support = Horizontal Ax + Vertical Az, Moment MA, Roller = Vertical Bz
Example
Formula cheat sheet of internal forces of a beam with a fixed and roller support
Conclusion
Now, that you got an understanding of what type of beams we use in structural engineering, you can learn about loads, because every beam is exposed to load.
Because there are always multiple loads acting on a beam. Considering these different loads in the structural design is done by setting up Load Combinations with safety factors.🦺
Once all load cases and combinations are set up, the structural elements can be designed. We have already written a lot of guides on how to design beams. Check them out.
I hope that this article helped you understand the different types of beams and how to do further from here. In case you still have questions.
Let us know in the comments below ✍️.
Beam Structure FAQ
Beams are horizontal elements which carry loads mostly perpendicular to its axis to distribute them to its supports. One characteristic of beams is that they act in bending, which occurs when loads act perpendicular to the element axis.
The 3 most common beams are
– Cantilever beam
– Simply supported beam
– Continuous beam
![Howe Truss [A Structural Guide]](https://www.structuralbasics.com/wp-content/uploads/2022/12/Howe-truss-768x439.jpg)