Dead Load – What Is It And How To Calculate It?

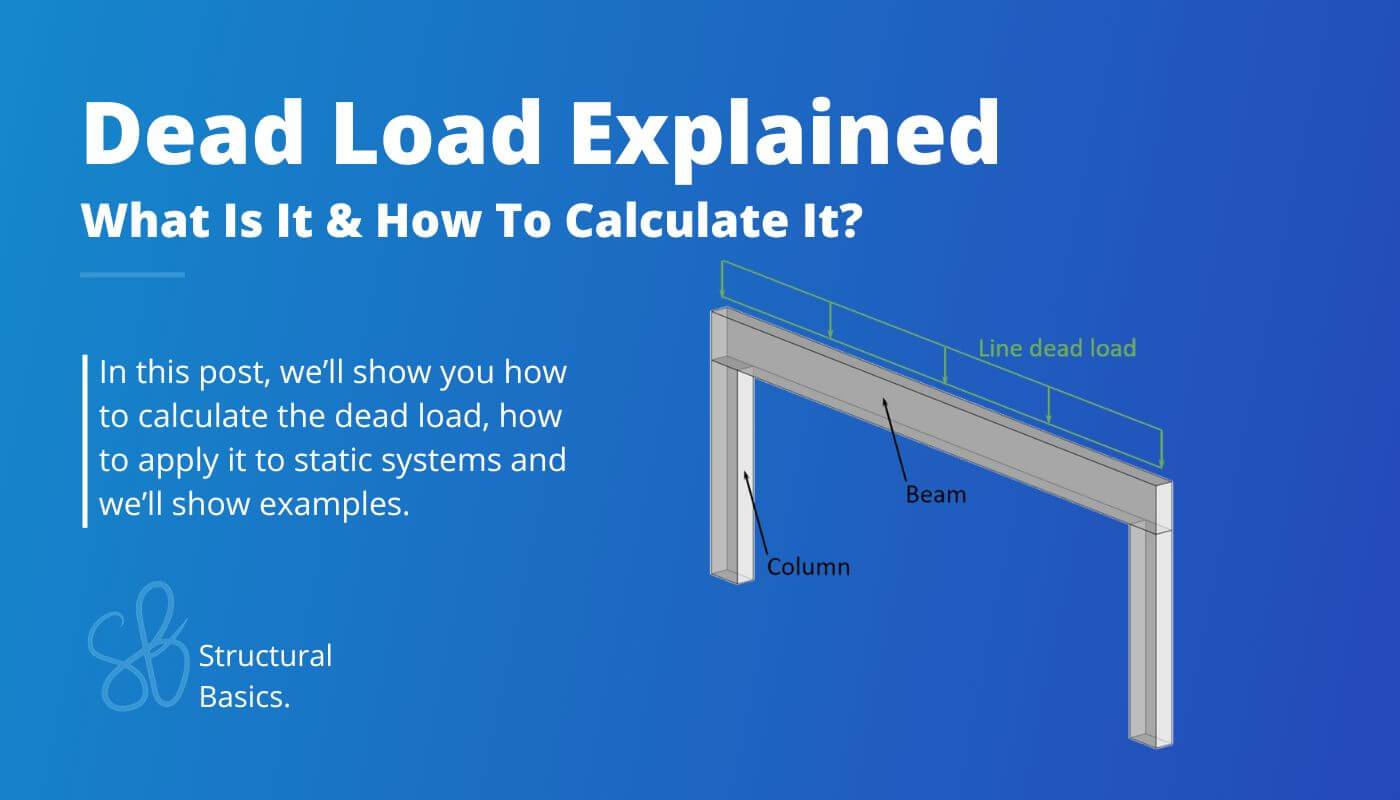
In short: The dead load is the self-weight of all elements of a building or structure, such as a concrete beam, flooring or the roof. The dead load is one of many structural loads that needs to be considered in a structural design.

Being a structural engineer myself, I am calculating dead loads for every project.

So in this article, I’ll show you, what the dead load is, examples of the dead load and how to calculate the dead load.

If you prefer video, then you can also watch our YouTube tutorial.

Let’s get started. 🚀🚀

What Is The Dead Load?

The dead load refers to permanent loads which act on a building, such as the self-weight of structural elements (like concrete slabs and steel beams) and non-structural building components (like roofing, windows and flooring). The weight is calculated and then applied to the structural member that carries it.

In structural design, this weight – the dead load – is a constant factor to make the calculation more straightforward. Each element in a building contributes to the dead load.

So, if you’re doing a renovation project and you, for example, increase the weight of your floor, you should consult with a structural engineer whether the slab can resist the additional load.

Calculation of Dead Load

How the dead load is calculated depends on the structural element that needs to withstand the load.

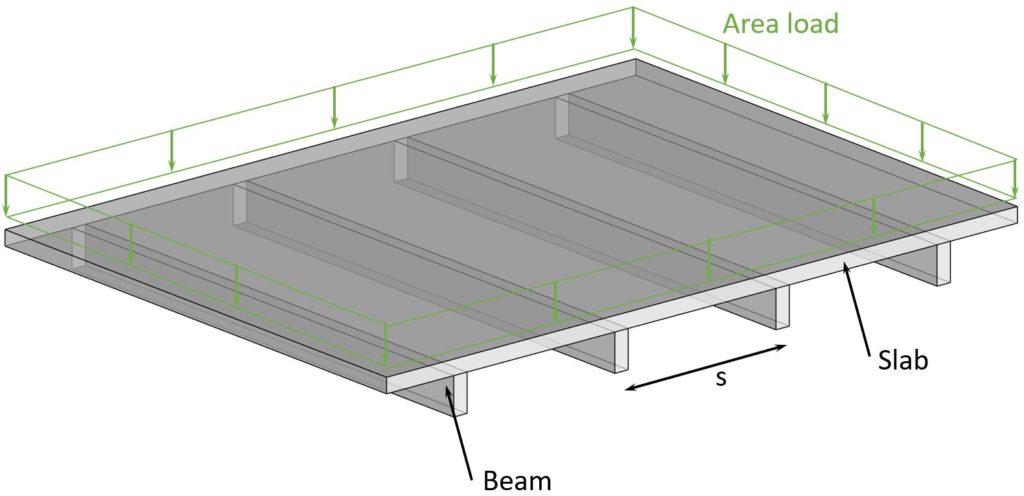
For example, the dead load of a slab is usually calculated as an area load (kN/m²) because the slab itself – 2D static element – needs to carry the load.

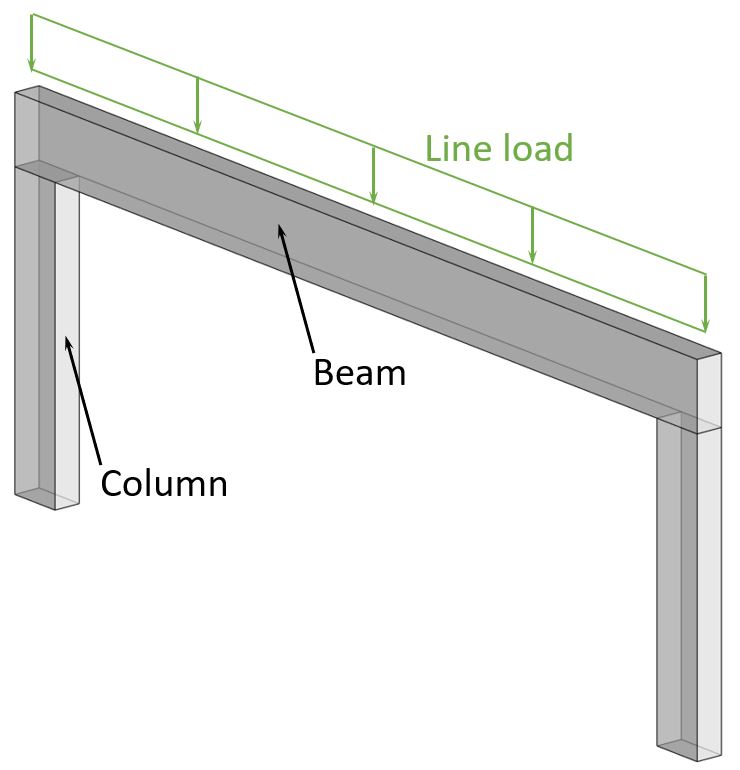
On the other hand, the dead load applied on 1D static elements like beams, columns, rods, etc. are usually either line (kN/m) or point loads (kN).

So let’s have a look at how to calculate the different dead load types. 👇👇

Area dead load

Example

The Area dead load of a concrete slab with a density of 2400 kg/m³ and a thickness of 18 cm is calculated as

$$g_k = 2400 \frac{kg}{m^3} \cdot 0.18m = 432 \frac{kg}{m^2} $$

Now, as engineers don’t use kg in their calculations any more, the unit needs to be transferred from kg to kN [Kilonewton].

To get kN you need to multiply the result by 0.0098. Or if you are a bit lazier, in most structural engineering cases it’s enough to multiply it by 0.01

$$g_k = 432 \frac{kg}{m^2} = 4.24 \frac{kN}{m^2}$$

Line dead load

The dead load is used as a line load for beams.

Example

The line dead load of a wooden GL24h beam with a density of 420 kg/m³, cross-section width of 10cm and a cross-section height of 20cm is calculated as:

$$g_k = 420 \frac{kg}{m^3} \cdot 0.2m \cdot 0.1m = 8.4 \frac{kg}{m} $$

As for the Area load, the line load also has to be transferred from kg to kN.

$$g_k = 8.4 \frac{kg}{m} = 0.08 \frac{kN}{m}$$

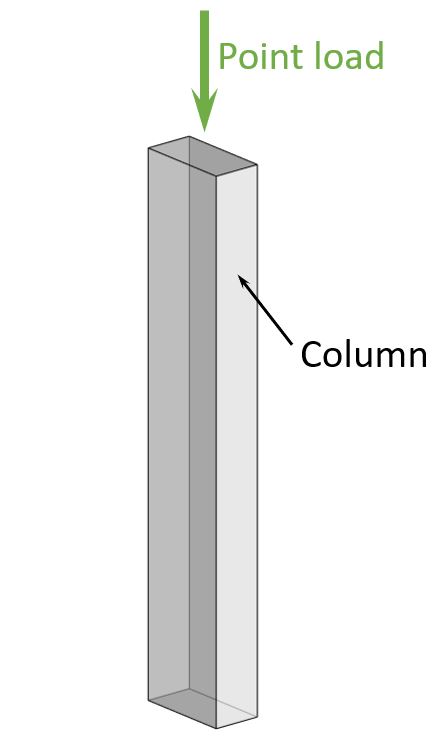
Point dead load

Example

An example where the dead load is calculated as a point load ($kN$) are columns. So in this case, we are calculating the dead load of a wood column.

The point dead load of a wooden GL24h column with a density of 420 $\frac{kg}{m^3}$, Cross-section width of 50cm, a Cross-section height of 50cm and a length of 3m is calculated as

$$g_k = 420 \frac{kg}{m^3} \cdot 0.5m \cdot 0.5m \cdot 3m = 315 kg $$

As for the line load, the point load also has to be transferred from kg to kN.

$$g_k = 315 kg = 3.1 kN$$

Example Calculation Of The Dead Load Of A Floor

In this section, I’ll show you how I as a structural engineer calculate the dead load of a floor. The floor layers are usually given by the architect.

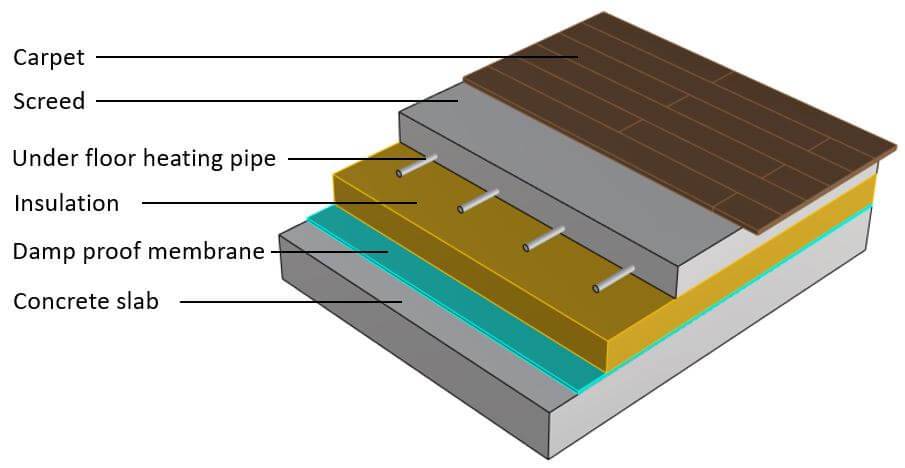
To calculate the dead load of each layer, I advise you to google either the density of the material or check if the product specifies its weight.

For example, by googling, I found that Rockwool insulation varies from 22 kg/m3 to 1000 kg/m3 in density. So pick a specific product and find its density. Or if you don’t know yet which product you use, it’s always a good idea to find 3 values from different manufacturers and use the highest density in your calculation.

You calculate the dead load for each layer individually and then add up the values to get the area dead load which you have to apply to the slab.

Floor layer	Thickness [mm]	Density [kg/m3]	Area load [kN/m2]
Concrete slab	200	2400	4.71
Insulation	200	42	0.39
Perlite screed	200	1000	1.96
Floor finish	15	660	0.1
Sum			7.16

Examples of Dead Load

Here are some examples of building materials which need to be considered in the dead load if used:

• MEP equipment
• Staircases
• Steel, concrete & wood beams
• Elevators
• Glass windows and panels
• Facade elements
• Timber & concrete slabs
• Insulation
• Roofing
• Bricks
• Tiles
• Ventilation ducts
• Steel, concrete & wood columns
• Heating systems
• Solar panels
• Garage ramps
• etc.

Just to mention, a few 😎.

As already explained above, depending on which structural element the building element is attached to an area, line or point load needs to be calculated from the density.

Some product manuals include the information of how much the element weighs.

Dead Load Direction

Now that we know how to calculate the dead load and its different types, we have to take a look at how to apply it to structural members.

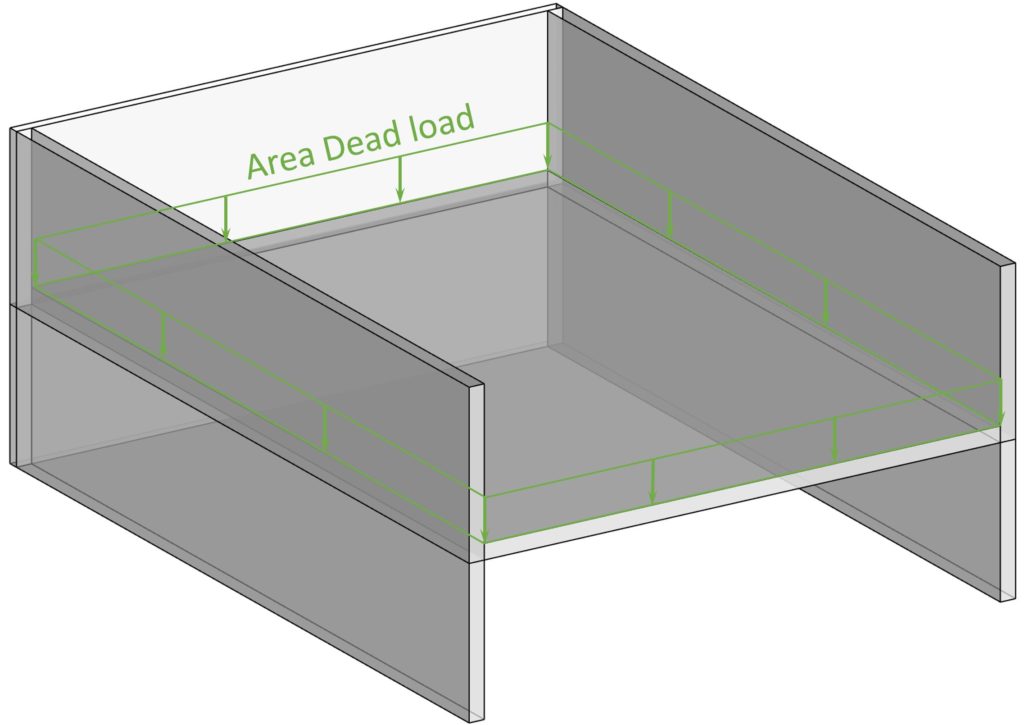
In most cases the dead load is applied to a horizontal element like for example a slab, balcony, flat roof, stairs.

And in that case the dead load can simply be applied vertically, as in the next picture, where a floor slab is supported on 3 edges by walls.

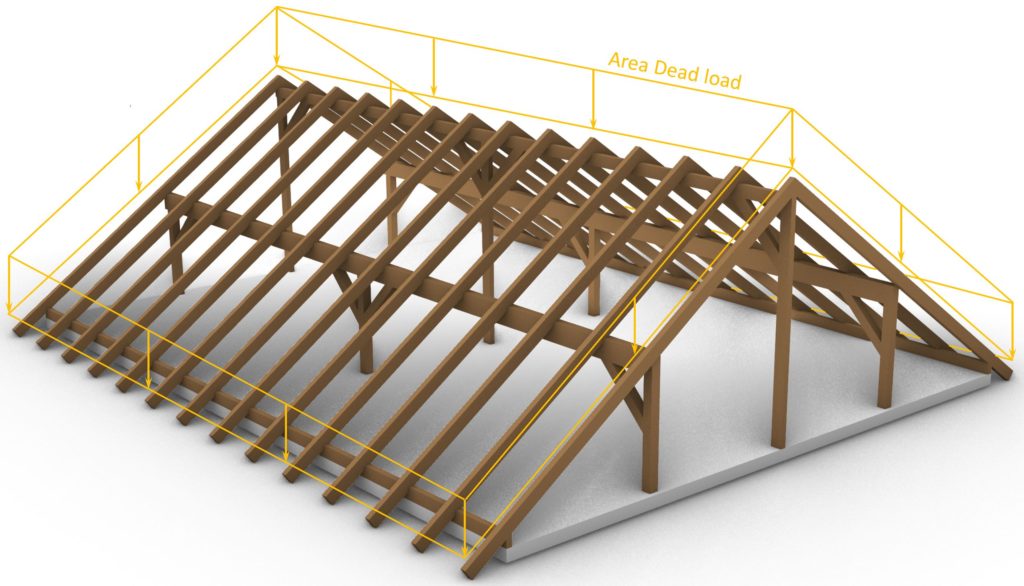
Now, it gets a bit more tricky when we need to apply the dead load to an inclined structural member like a rafter roof. We wrote an extensive article about loads on roof structures, and you can check it out here.

But the short version: The dead load gets applied to inclined structures, like the live load.

The load direction is z-axis downwards ⬇️, while the distribution follows the inclination of the roof.

Unit

The unit of the dead load in Europe is one of the following:

• Area load: $kN/m^2$ = Kilonewton per square meter
• Line load: $kN/m$ = Kilonewton per meter
• Point load: $kN$ = Kilonewton

Conclusion

Now, that you got an understanding of what the dead load is and how it is used, it’s time to look at other loads like

• Snow load
• Wind load

Because there are always multiple loads acting on a structural element. Considering these different loads in the structural design is done by setting up Load Combinations with safety factors.

Once all load cases and combinations are set up, the structural elements can be designed. We have already written a lot of guides on how to design structural elements. Check them out.

• Structural design of a timber beam
• Structural design of a timber purlin roof
• Structural design of a timber column

I hope that this article helped you understand the dead load. In case you still have questions. Let us know in the comments below ✍️.