Understand Shear Forces [An Engineering Explanation]

Do you need to calculate shear forces in uni but didn’t understand a thing? 🤔🤔

It’s indeed difficult. It took me personally 2-3 months to fully understand it.

So in this blog post, we’ll explain what a shear force is and how to calculate it step-by-step.👍👍

We’ll also add real-world examples, which you usually don’t see in uni. 👀👀

Alright, let’s get started. 🚀🚀

What Is The Shear Force?

A shear force describes the internal force that acts parallel to a surface trying to slide or deform one part of a surface relative to another.

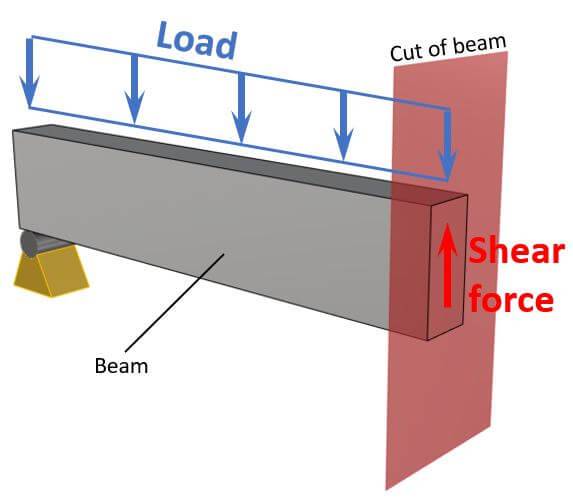
In easier words, if you are trying to slide a heavy book on a table with only one finger and not a lot of force (pushing) and the book is not moving in the direction you are pushing, then the shear resistance of the table is bigger than the shear force (your pushing).

Now, let’s get a bit more technical.

Shear forces appear at any location of the beam, and it’s visualized as an arrow. ⬇️⬇️

As it appears at any point of the beam, we cut the beam. This is done to calculate the internal forces, such as shear forces at the point of the cut. We have already written a more detailed article about the internal force calculation.

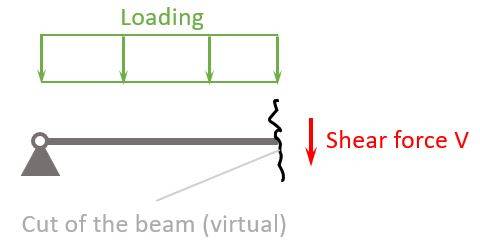
Due to this shear force, the beam experiences a shear stress.

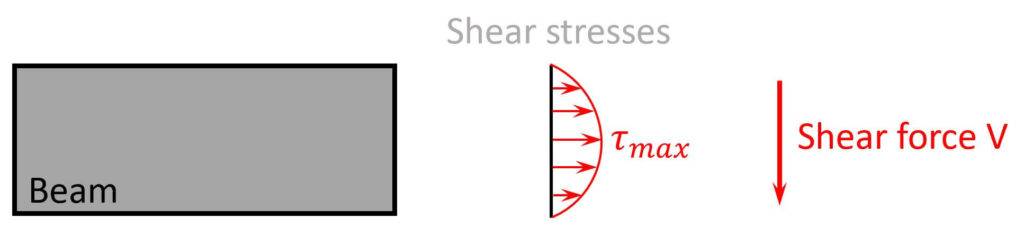
In the picture, you can also see that the biggest stresses appear in the centre of the cross-section.

The beam fails if

$$\tau_{max} > \tau_{resistance}$$

where $\tau_{resistance}$ is the shear stress resistance of the beam/material.

And as you can imagine, the bigger the shear force, the bigger the shear stress.

But how does the shear force increase?

Well, we’ll calculate the shear force in a second, but in general we can say that it increases due to increased

• loading
• span
• stiffness

Now, let’s have a look at how we determine the magnitude of a shear force. 👇👇

Shear Force Calculation

Shear forces are calculated as the sum of all forces in the direction of the shear force. In our example beam that is the vertical direction, as it is the case for most beams.

$$\sum V = 0$$

Alright, let’s do that for an example. 👇👇

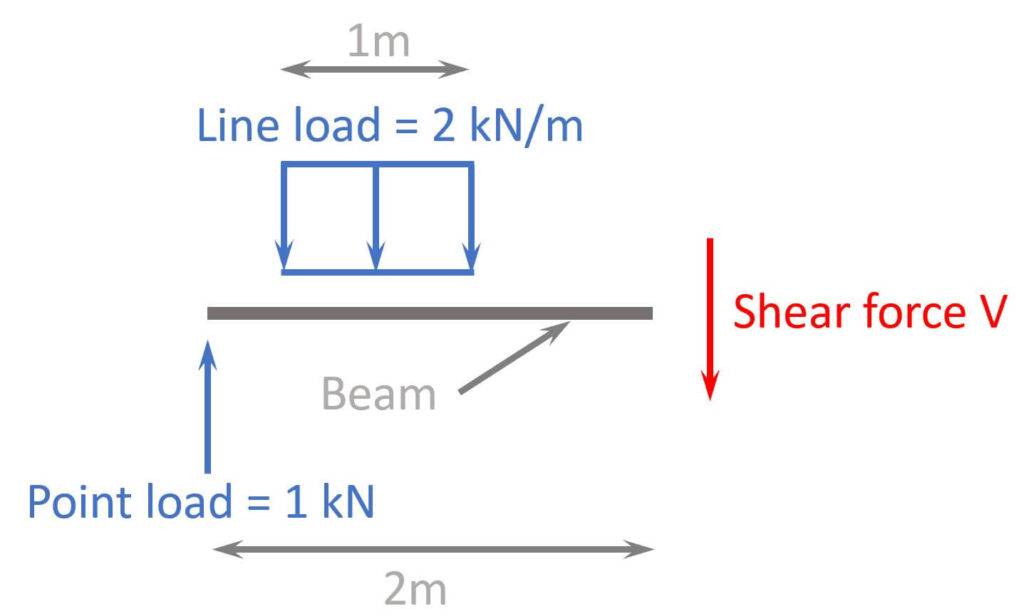
So the shear force V in a specific point of a beam element is calculated as the sum of all forces equal to 0.

We define upwards ⬆️⬆️ as the positive direction ➕➕. But you could also pick downwards ⬇️⬇️ as the positive direction. The result will be the same.

$$\sum = 0: 1 kN – 2 kN/m \cdot 1 m – V = 0$$

Now let’s solve that for the unknown shear force V.

$$V = 1 kN – 2kN/m \cdot 1 m = – 1 kN$$

This was just an example of a small part of a beam to get started.

We can now move on and look at a full calculation example of a beam. 👇👇

Calculation Example

We now can calculate the shear force of a simply supported beam which is subjected to a line load.

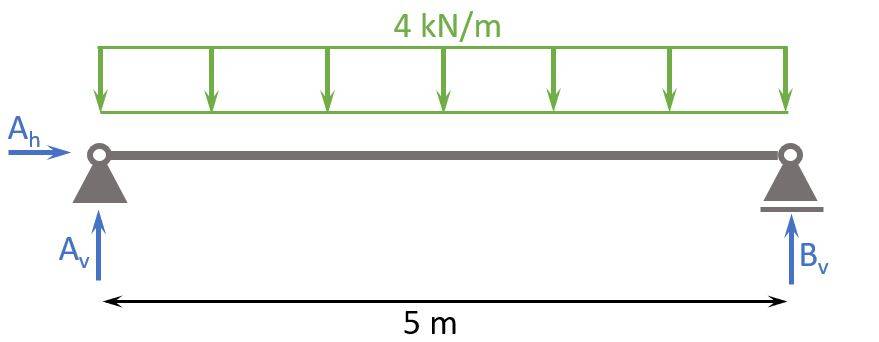
Here are the steps, we are going to follow to calculate the shear forces:

1. Calculation of the reaction forces

We use moment equilibrium in point b to calculate A_v, because the support in point b is a hinge and therefore the moment = 0.

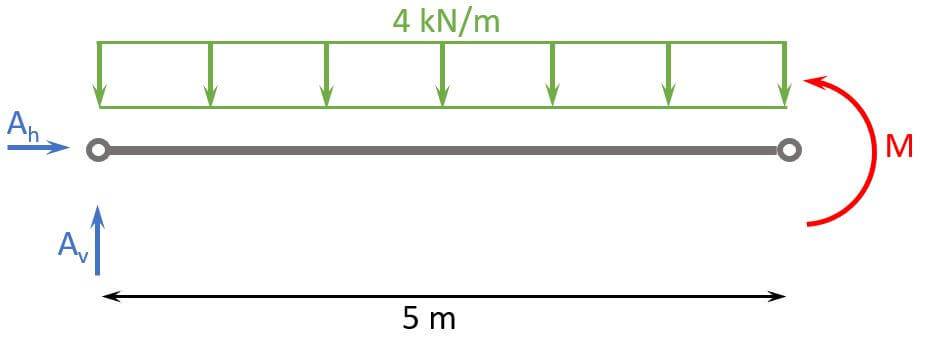
$$\sum M = 0: A_v \cdot 5m – 4 kN/m \cdot 5m \cdot \frac{5m}{2} + M = 0$$

As already said, M = 0 and therefore

$$A_v \cdot 5m = 4 kN/m \cdot 5m \cdot \frac{5m}{2}$$

$$A_v = 4 kN/m \cdot \frac{5m}{2} = 10 kN$$

We use vertical equilibrium to calculate B_v.

$$\sum V = 0: A_v + B_v – 4 kN/m \cdot 5m = 0$$

$$B_v = – A_v + 20 kN = 10 kN$$

2. Cut the beam at a location x

Let’s make the first cut at x=3m.

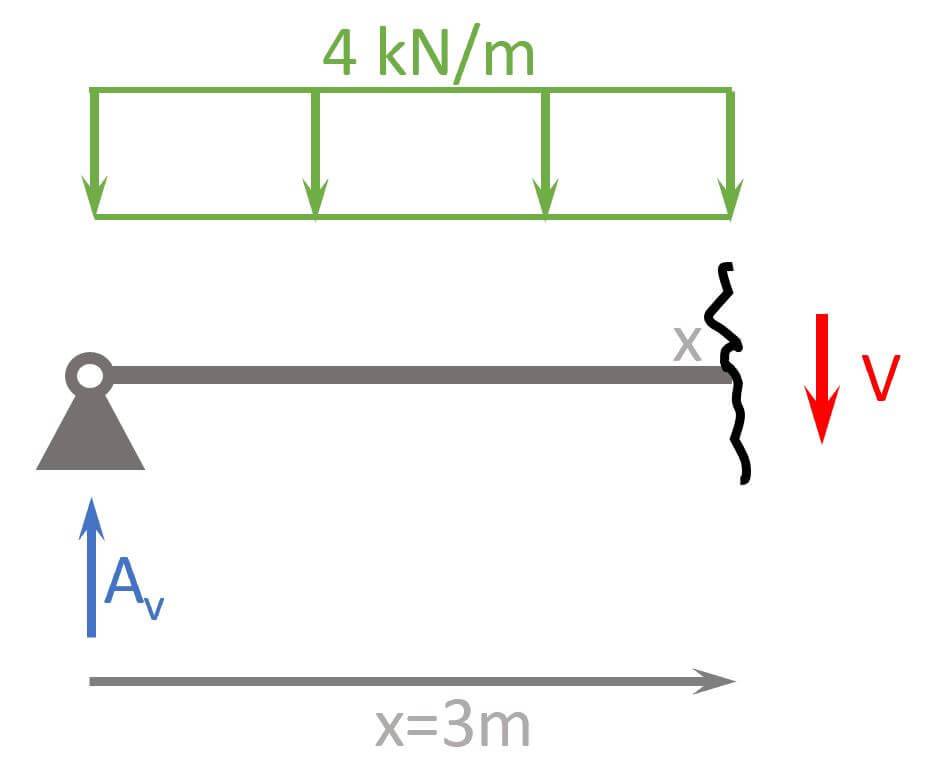
3. Calculate the shear force at location x

We use the vertical force equilibrium to calculate V at x=3m.

$$\sum V = 0: A_v – 4 kN/m \cdot 3m – V = 0$$

$$M = 10 kN – 4 kN/m \cdot 3m = -2 kN$$

4. Calculate the shear forces at different locations

Alright, let’s also calculate V at x=2m and x = 4.5m.

x=2m

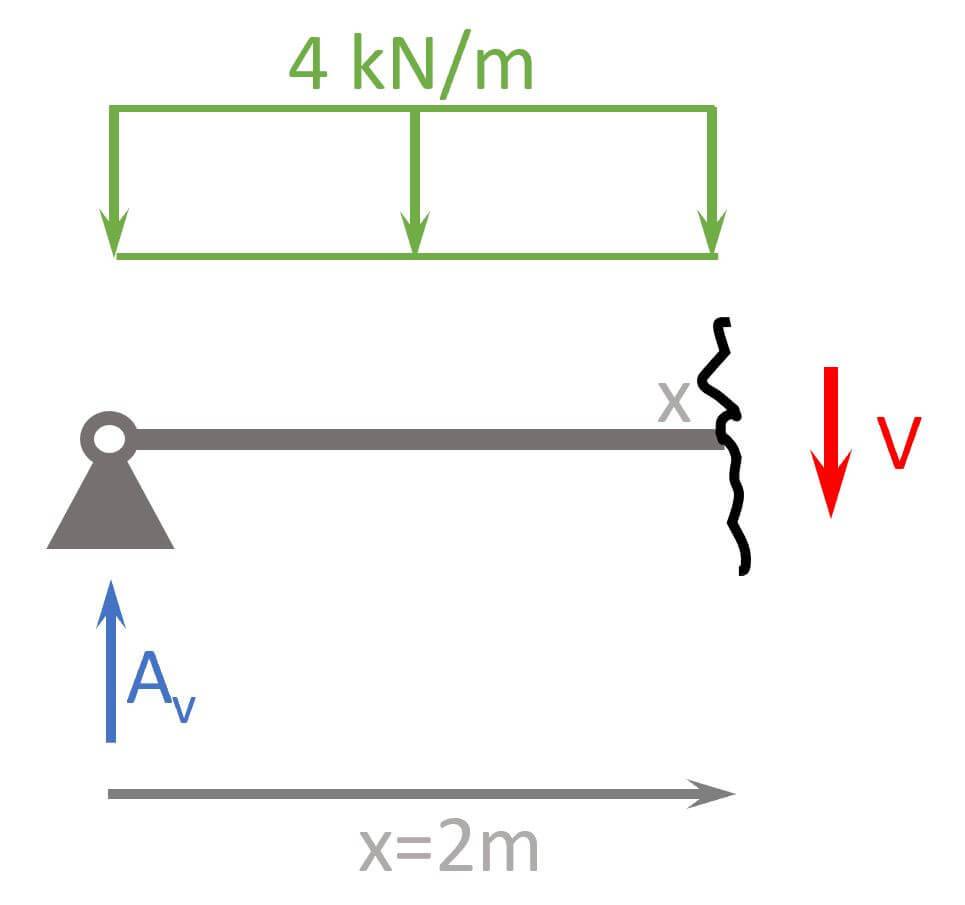
$$\sum V = 0: A_v – 4 kN/m \cdot 2 m – V = 0$$

$$V = 10 kN – 4 kN/m \cdot 2m = 2 kN$$

x=4.5m

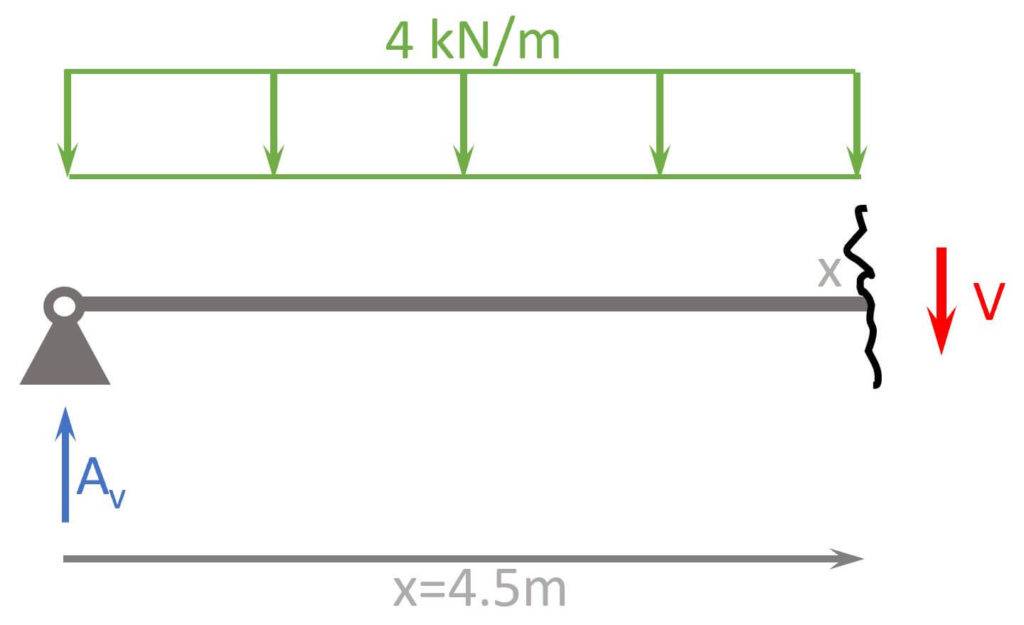
$$\sum V = 0: A_v – 4 kN/m \cdot 4.5 m – V = 0$$

$$V = 10 kN – 4 kN/m \cdot 4.5m = -8 kN$$

Alright, we could continue and calculate the moments at other points as well, but I think you understood how it works.

In our case, the shear forces at supports A and B = 10 kN.

Now, let’s move on and visualize the results. 🚀🚀

Shear Force Diagrams

A great visualization of the calculated results is a shear force diagram. The following diagram visualizes the shear forces of the example above.

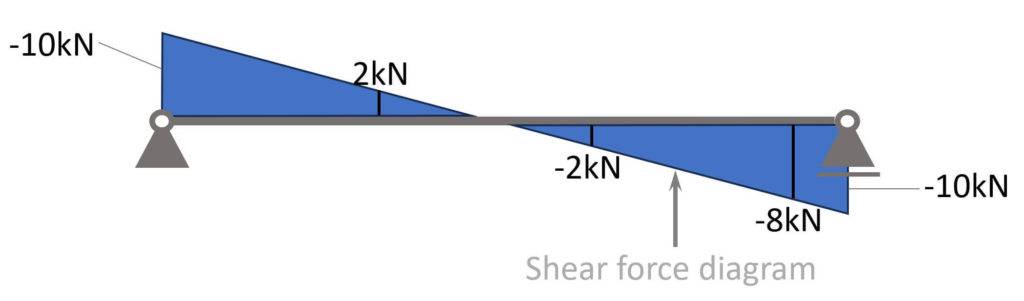
To create a shear force diagram, we simply plot the values from the shear force equation.

Don’t worry, you don’t have to do that manually later on. Software programs help us with that!

Shear Force Formulas

For the most used static systems, there are luckily formulas that help us to calculate the shear forces. We covered them extensively in the following articles:

• Shear force formulas of the simply supported beam
• Shear formulas of cantilever beams
• Shear formulas of the 2-span continuous beam

So we’ll just mention the most important ones in this article.

Simply Supported Beam With Line Load

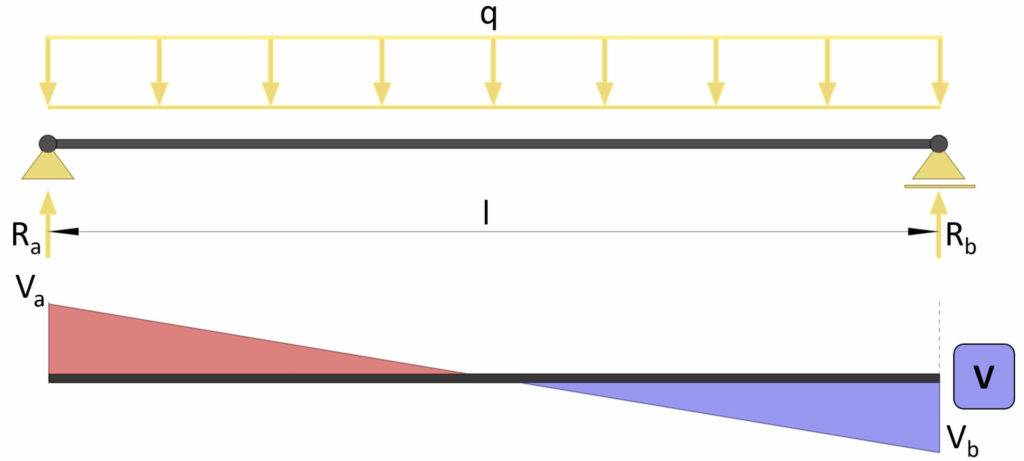
Max shear force

$$V_{max} = \frac{1}{2} \cdot q \cdot l$$

Simply Supported Beam With Point Load

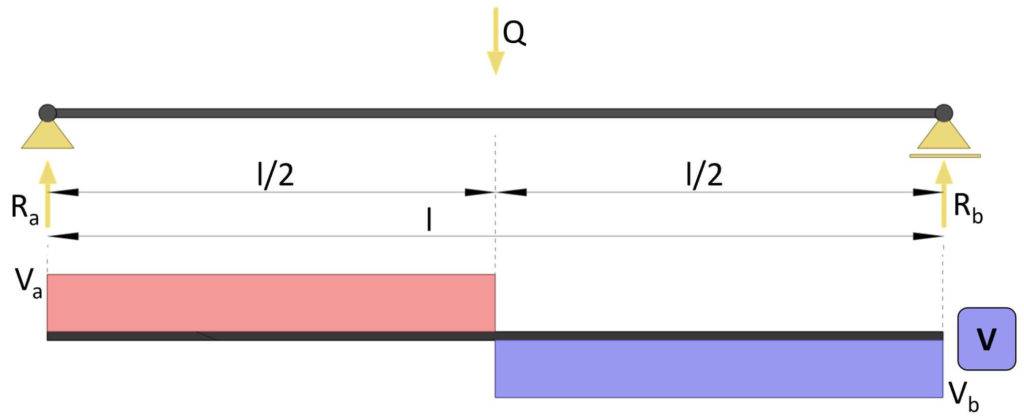
Max shear force

$$V_{max} = \frac{1}{2} \cdot Q$$

Moment Of Simply Supported Beam With 2 Point Loads

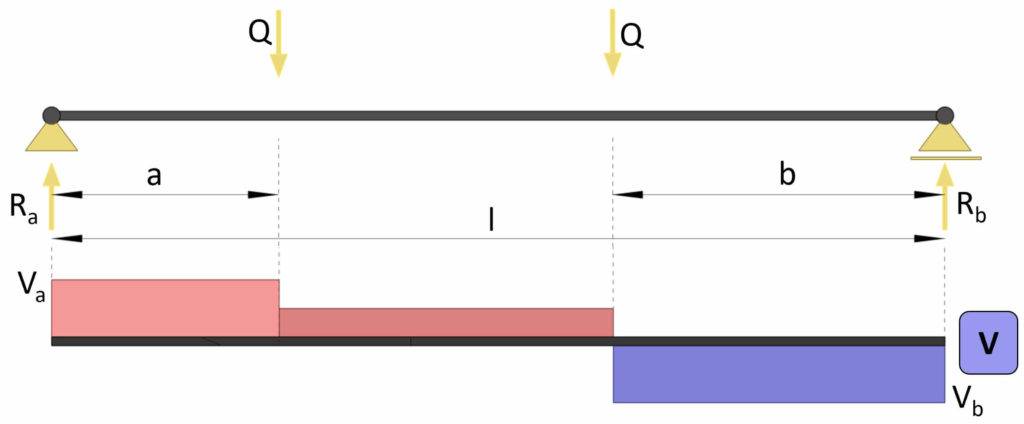
Shear forces at supports

$$V_{a} = \frac{Q}{l} \cdot (l – a + b)$$

$$V_{b} = – \frac{Q}{l} \cdot (l – b + a)$$

Moment Of Cantilever Beam Due To Line Load

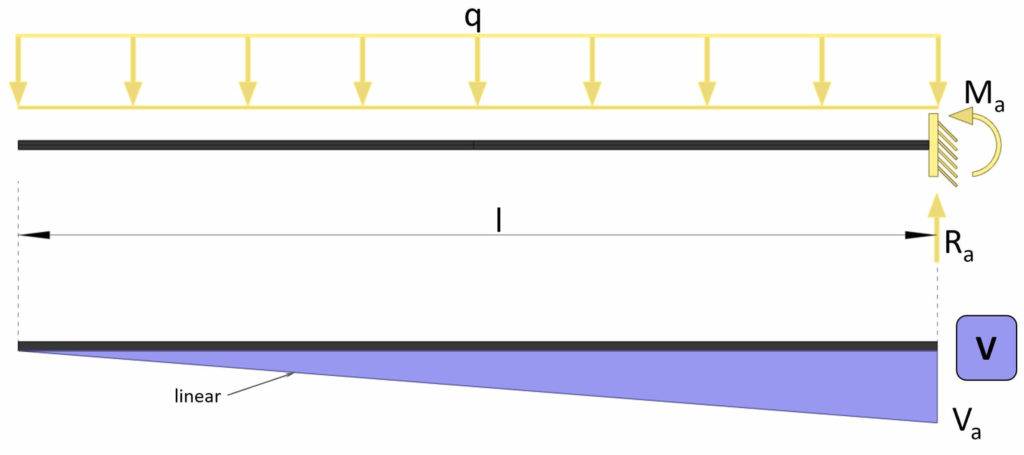
Max shear force

$$V_{max} = – q \cdot l$$

Shearing Force Examples

Now, let’s have a look at how shearing forces are used in structural engineering projects.

Design of flat roof timber beams

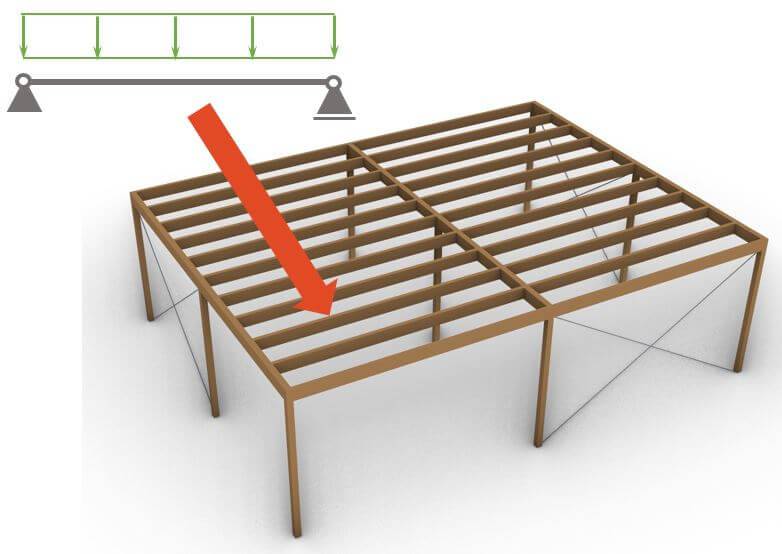
The timber beams that you can see in the picture above are calculated as a simply supported beam. External loads like snow, dead and wind load are applied to the beam and the shear force is calculated to dimension the size of the timber beams or to verify that the beam doesn’t fail.

We showed everything step-by-step in this article.

Design of foundations

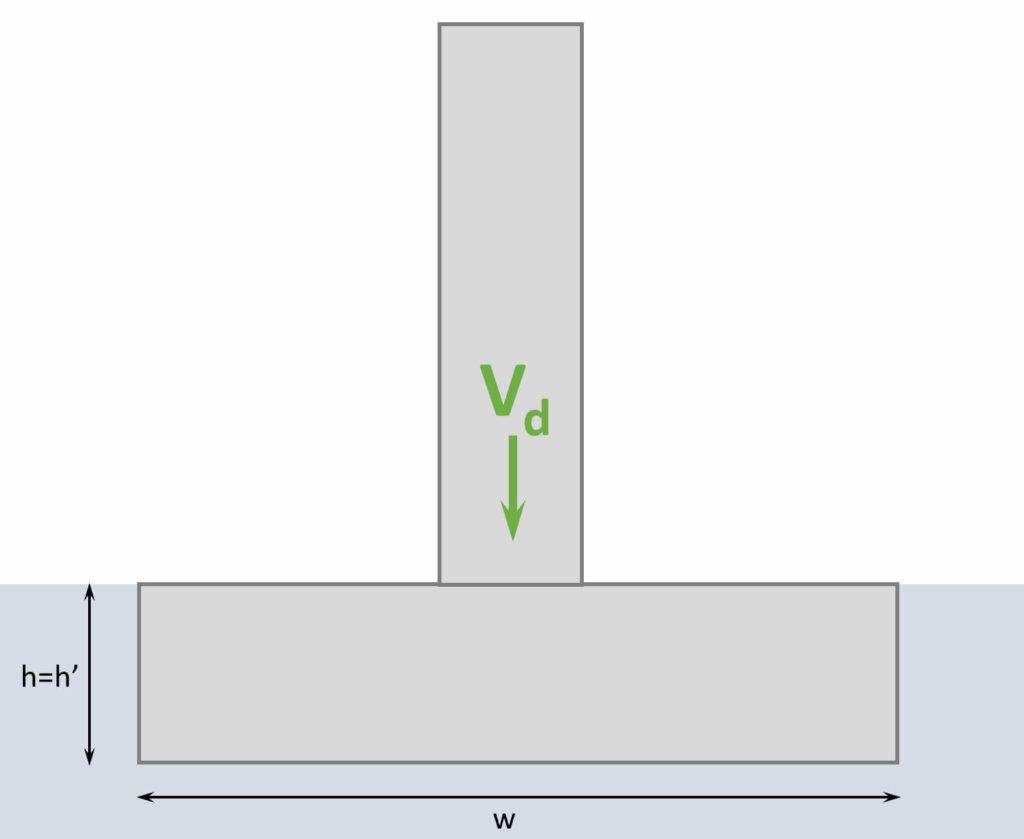
The pad foundation (horizontal element) in the picture above is exposed to the vertical load V_d. Due to this load, the pad is subjected to shearing forces which need to be resisted. Either the shear resistance of the foundation is enough or shear reinforcement is added.

We show the design in our pad foundation guide.

Conclusion

Now, that you got an understanding of shear forces, you can learn about the other internal force – bending moment. Together, shear force and bending moment are used to design real structures such as

• Timber beams
• Timber purlins
• Steel beams

I hope that this article helped you, and you know how to go further from here. In case you still have questions.

Let us know in the comments below. ✍️✍️

Shear Force FAQ