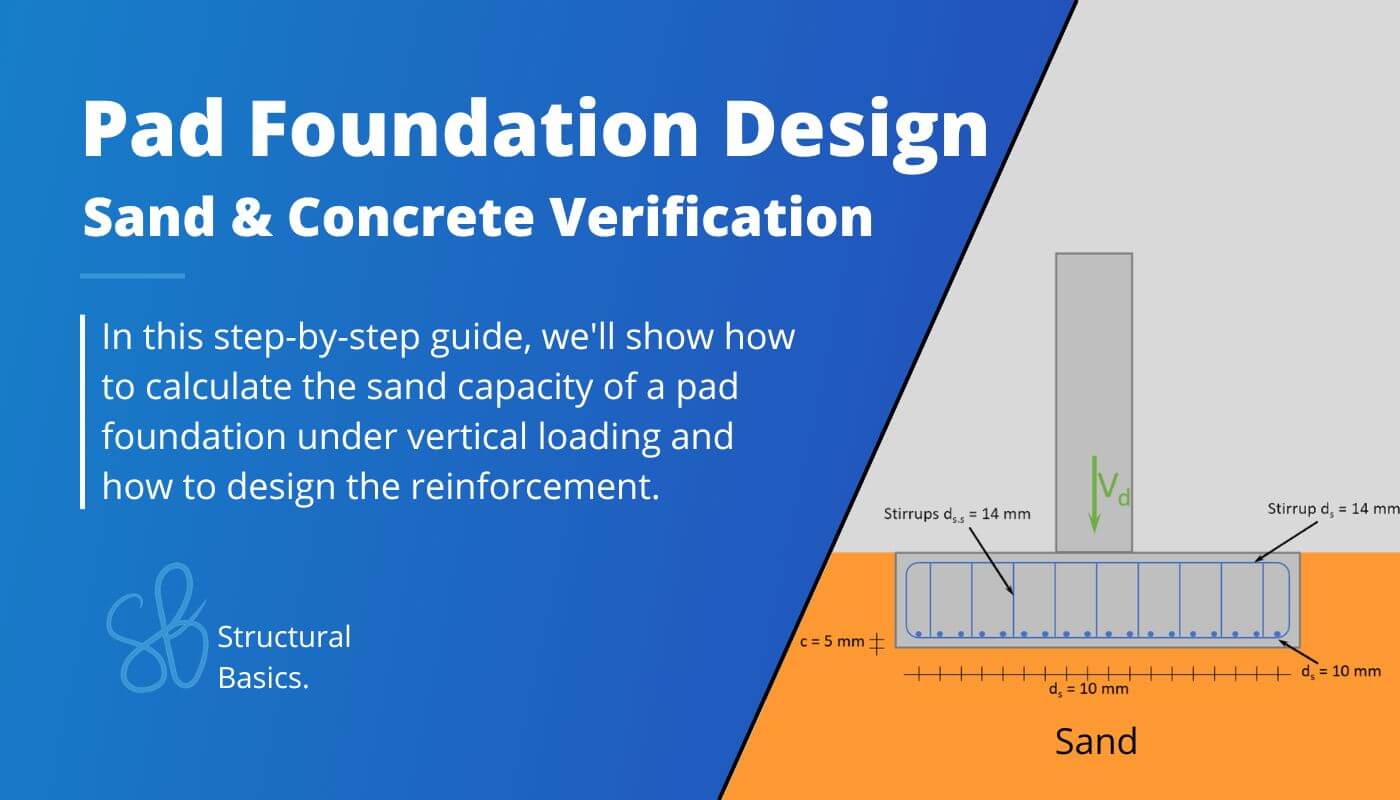
Pad Foundation Design: Sand & Concrete Verification Under Vertical Load
Designing a pad foundation is never really taught fully in university or textbooks. 🙈🙈
It’s either the geotechnical or the reinforced concrete design.
But both are necessary for structural documentation. 📄📄
That’s why in this post we’ll show you, step-by step, how to design a pad foundation embedded in sand with a worked example. We’ll cover both the geotechnical verification of sand according to Eurocode EN 1997-1 and the reinforced concrete verification according to Eurocode EN 1992-1-1.
Not much more talk, let’s dive into it. 🚀🚀
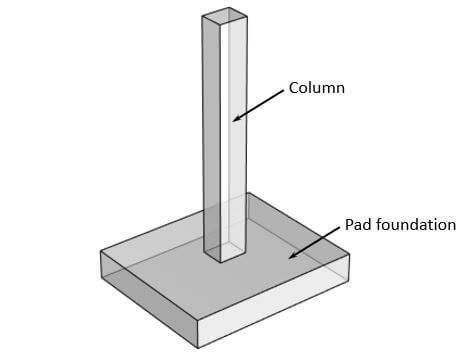
🙋♀️ What Is A Pad Foundation?
Pad foundations are used to support columns from buildings. They consist of a concrete “block”, and in most cases steel reinforcement to resist tensile forces. Pad foundations are placed on soil and spread the concentrated load from the column to a wider area of the soil.
Pad foundations can have different shapes, from circular 🔵🔵 to rectangular 🟦🟦 bases.
📃 Process of Pad Foundation Design
Before we dive into the nerdy calculations 😋😋, it’s good to get an overview of the steps that need to be taken to design a pad foundation, which is supported by sand and exposed to a vertical load.
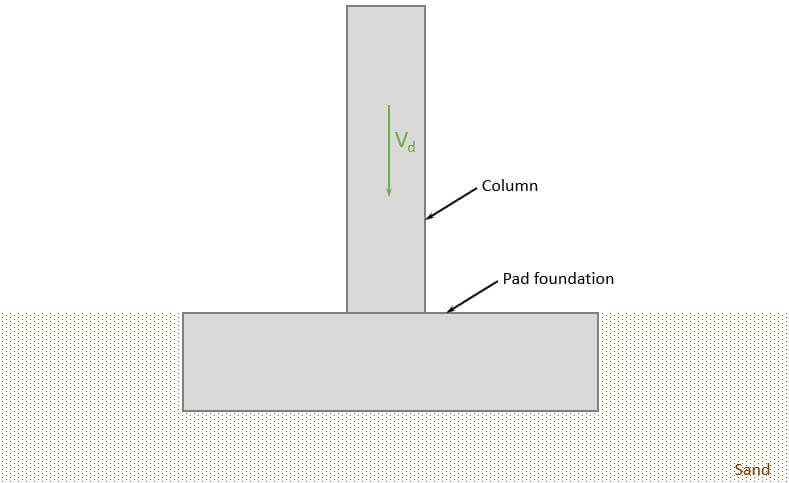
- Calculate characteristic loads that act on pad foundation
- Load combinations
- Define properties of the sand and concrete
- Geotechnical design – bearing resistance verification
- Reinforced concrete design – bending verification
- Reinforced concrete design – shear verification
⬇️ Characteristic Loads
The loads of a structure depend on its location, geometry, building type and other factors.
We’ll assume in this tutorial that we design the pad foundation of a multi-storey building. 👇👇
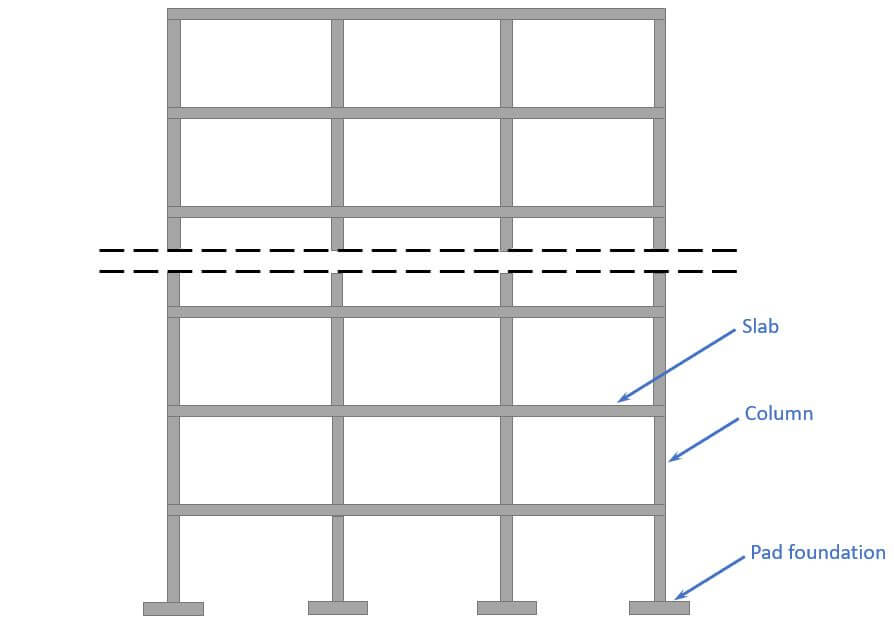
Now to calculate the characteristic loads acting on the pad foundation, we need to know what loads are applied where and how the loads travel through the different elements and to the foundations.
In this simplified design guide, the following vertical loads are considered:
- Dead load of structural (concrete slab) and non-structural elements (flooring, etc.)
- Live load
- Snow load
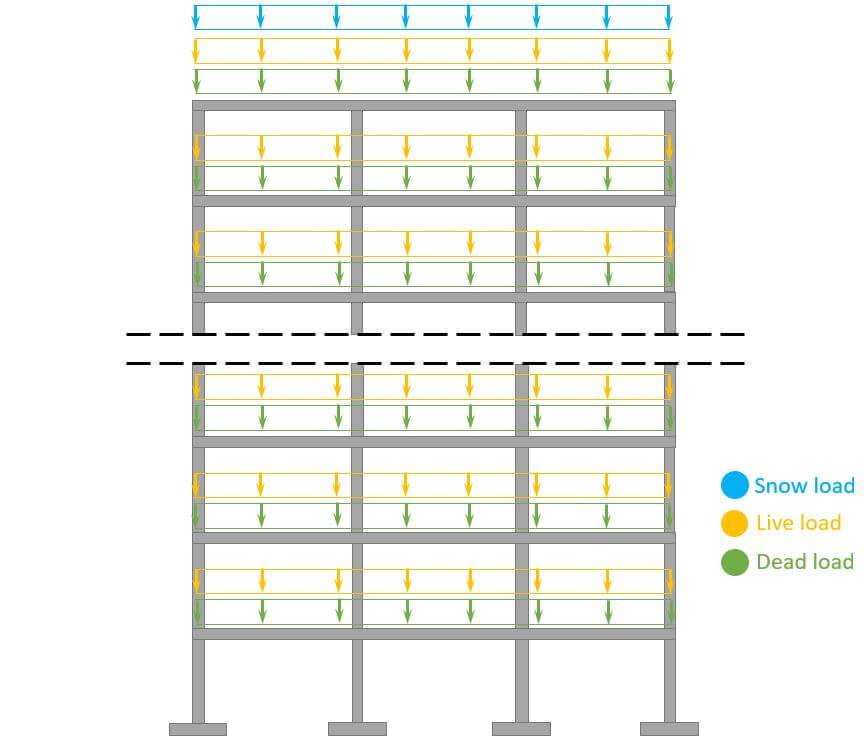
Now, in the structural design of such a building other loads are also considered such as seismic and wind load and imperfections.
But we’ll do a lot of assumptions in this tutorial. If you want to learn more about all the loads that act on a building, then check out this article.
Load transfer
❗ The following load transfer explanation works if the building is a traditional structure with simply supported beams and columns❗
- Live, snow and dead load (self-weight of roofing) are applied as area loads [kN/m2] on the roof. This could be precast hollow core slabs, which transfer the loads to beams.
- By multiplying the area loads (live, snow, dead load) with the spacing of the beams, line loads are calculated. These line load can now be applied to the beams.
- The reaction force of a beam is then the characteristic vertical load that is applied to the column which supports the beam.
- We do that for every floor, and the reaction forces are added up and applied to the pad foundation.
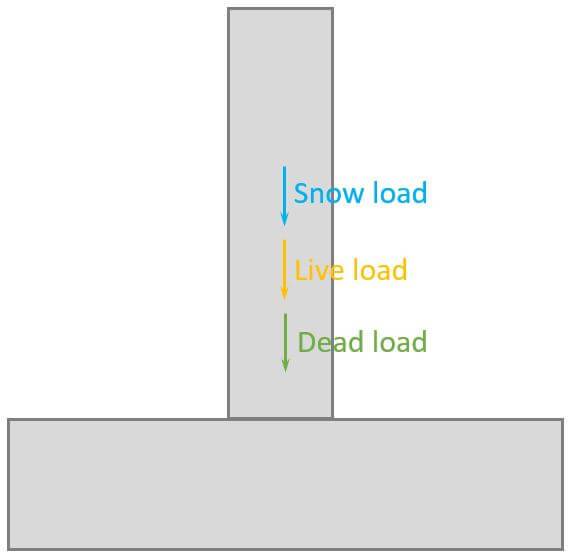
The following characteristic load values are assumptions.
| $g_{k}$ | 450 kN | Characteristic value of dead load |
| $q_{k}$ | 600 kN | Characteristic value of live load |
| $s_{k}$ | 15 kN | Characteristic value of snow load |
❗❗ The characteristic values of loads depend on a lot of different factors like location, National Annex and geometry of the building and roof to name just a few. Loads therefore need to be calculated for every structure. ❗❗
➕ Load combinations
Load combinations combine several load cases and multiply the characteristic loads with safety factors.
Check out our extensive article about load combinations to learn more about partial safety factors and how to set up the combinations.
ULS Load combinations
| LC1 | $1.35 \cdot 450 kN $ | $607.5 kN$ | |
| LC2 | $1.35 \cdot 450 kN + 1.5 \cdot 600 kN$ | $1507.5 kN$ | |
| LC3 | $1.35 \cdot 450 kN + 1.5 \cdot 600 kN + 0.6 \cdot 1.5 \cdot 15 kN$ | $1521 kN$ | |
| LC4 | $1.35 \cdot 450 kN + 1.5 \cdot 15 kN$ | $630 kN$ |
You can also use our load combination generator, which creates the load combinations automatically for you, and you can copy & paste the table into Word. 🔥🔥
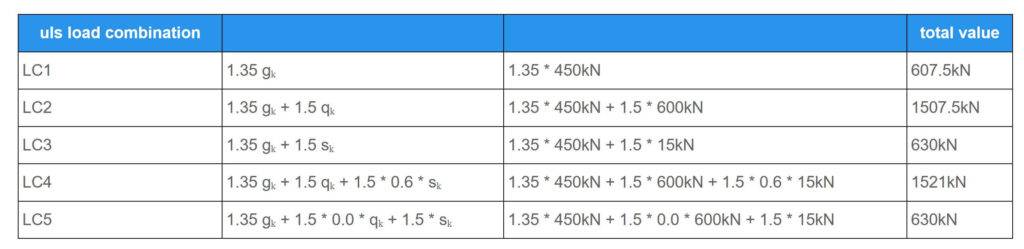
So the vertical design load we are designing the pad foundation for is:
$$V_{d} = 1521 kN$$
🟫 Geotechnical Soil Properties
The pad foundation is embedded into the soil. In our example, it’s sand.
For this tutorial, we use the following soil properties.
| Density sand | $\gamma_{sand} = 18 kN/m^3$ | |
| Angle of friction | $\varphi = 35 \deg$ | |
| Partial factor (shearing resistance) Depends on the country | $\gamma_{\varphi} = 1.2$ | |
| Design angle of friction | $\varphi ‘ = atan( \frac{tan(\varphi)}{\gamma_{\varphi}}) = 30.26 \deg$ | |
| Density water | $\gamma_w = 10 kN/m^3$ | |
| Density wet sand | $\gamma’ = \gamma_{sand} – \gamma_w = 8 kN/m^3$ |
⬜ Concrete and Reinforcement Properties
For this tutorial, we use the following concrete and reinforcement properties.
| Concrete compression strength | $f_{c.k} = 30 MPa$ | |
| Concrete tensile strength | $f_{ctm} = 2.9 MPa$ | |
| Partial factor – in-situ Depends on the country | $\gamma_{c} = 1.45$ | |
| Design concrete compression strength | $f_{c.d} = \frac{f_{c.k}}{\gamma_{c}} = 20.7 MPa$ | |
| Design concrete tensile strength | $f_{c.t} = \frac{f_{ctm}}{\gamma_{c}} = 2.0 MPa$ | |
| Reinforcement yield strength | $f_{y.k} = 550 MPa$ | |
| Density concrete | $\gamma_c = 24 kN/m^3$ | |
| Concrete cover | $c = 50 mm$ | |
| Partial factor – reinforcement Depends on the country | $\gamma_{s} = 1.2$ | |
| $\epsilon_{cu3} = 0.35%$ | ||
| $\epsilon_{c3} = 0.175%$ | ||
| $\lambda = 0.8$ | ||
| $\epsilon_{yd} = 0.208%$ | ||
| $\eta = 1.0$ |
🕵️♂️ Geometry Of The Foundation And Column
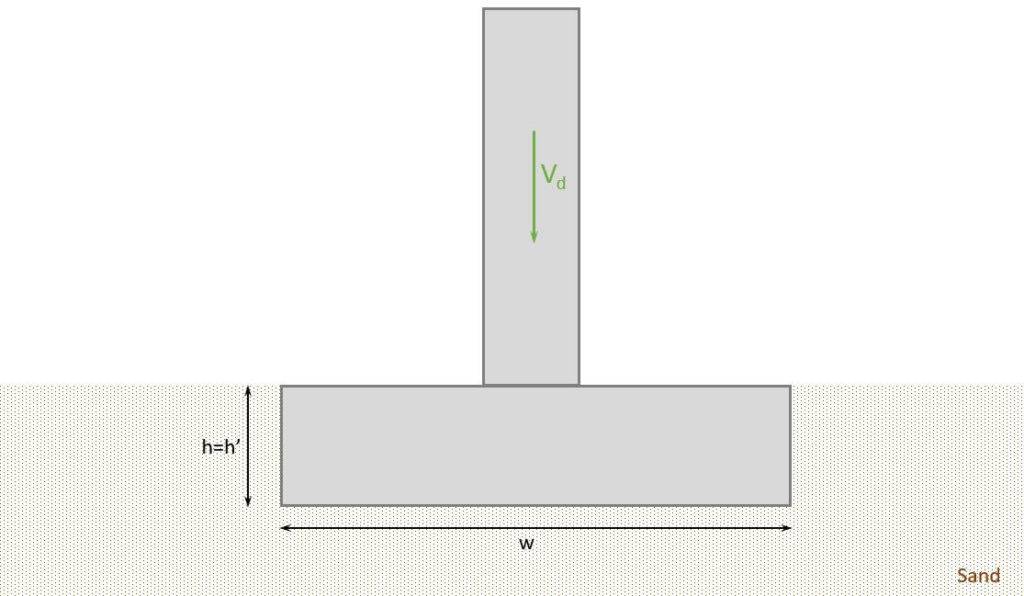
| Width | $w = 2.1 m$ | |
| Length | $l = w = 2.1 m$ | |
| Height | $h = 0.5 m$ | |
| Depth of embedded foundation | $h’ = h = 0.5 m$ | |
| Width of column | $w_c = 0.4 m$ | |
| Inclination of the foundation base to the horizontal | $\alpha = 0$ | |
| Dead load of foundation (self-weight) | $G_k = w \cdot l \cdot h \cdot \gamma_c = 52.9 kN$ | |
| New vertical design load | $V_d = V_d + 1.35 \cdot G_k = 1592 kN$ |
Now, in countries, where the temperatures can get low, it’s common to have a minimum depth, where frost can’t affect the groundwater any more. Because if it does, it can lift up the foundation.
In Denmark, for example, 0.9 m is a common minimum depth.
✍️ Geotechnical Design – Bearing Resistance (EN 1997-1)
As we only have a vertical load acting on the pad foundation, we only have to verify that the design bearing resistance of the sand is greater than the design load. Let’s do that. 👍👍
For the final formula, we first need to calculate a lot of factors.
Bearing resistance factors (EN 1997-1 (D.2))
$$N_q = e^{\pi \cdot tan(\varphi ‘)} \cdot tan(45 deg + \frac{\varphi ‘}{2})^2 = 18.96$$
$$N_{\varphi} = 2 \cdot (N_q – 1) \cdot tan(\varphi ‘) = 20.96$$
Shape factors (EN 1997-1 (D.2))
$$s_q = 1 + \frac{w}{l} \cdot sin(\varphi ‘) = 1.504$$
$$s_{\varphi} = 1 – 0.3 \cdot \frac{w}{l} = 0.7$$
Inclination of loads (EN 1997-1 (D.2))
$$i_q = (1 – \frac{H_d}{V_d})^2 = 1$$
$$i_{\varphi} = (1 – \frac{H_d}{V_d})^{\frac{3}{2}} = 1$$
Inclination of the foundation base (EN 1997-1 (D.2))
$$b_q = (1 – \alpha \cdot tan(\varphi ‘))^2 = 1$$
$$b_{\varphi} = b_q = 1$$
Effective vertical stress
$$q = \gamma_{sand} \cdot h’ = 9 kN/m^2$$
Design bearing resistance (EN 1997-1 (D.2))
$$\frac{R}{A} = q \cdot N_q \cdot b_q \cdot s_q \cdot i_q + \frac{1}{2} \cdot \gamma ‘ \cdot w \cdot N_{\varphi} \cdot b_{\varphi} \cdot s_{\varphi} \cdot i_{\varphi} = 379.9 kN/m^2$$
$$R_d = 427.4 kN/m^2 \cdot w \cdot l = 1675 kN$$
Utilization
$$\eta = \frac{V_d}{R_d} = \frac{1592 kN}{1675 kN} = 0.95$$
Therefore, the bearing capacity of the soil (sand) is verified. 👍👍
👨🔬 Reinforced Concrete Design – Bending Verification
A strut and tie model is used to transfer the point load to the soil and spread the load equally along the foundation base.
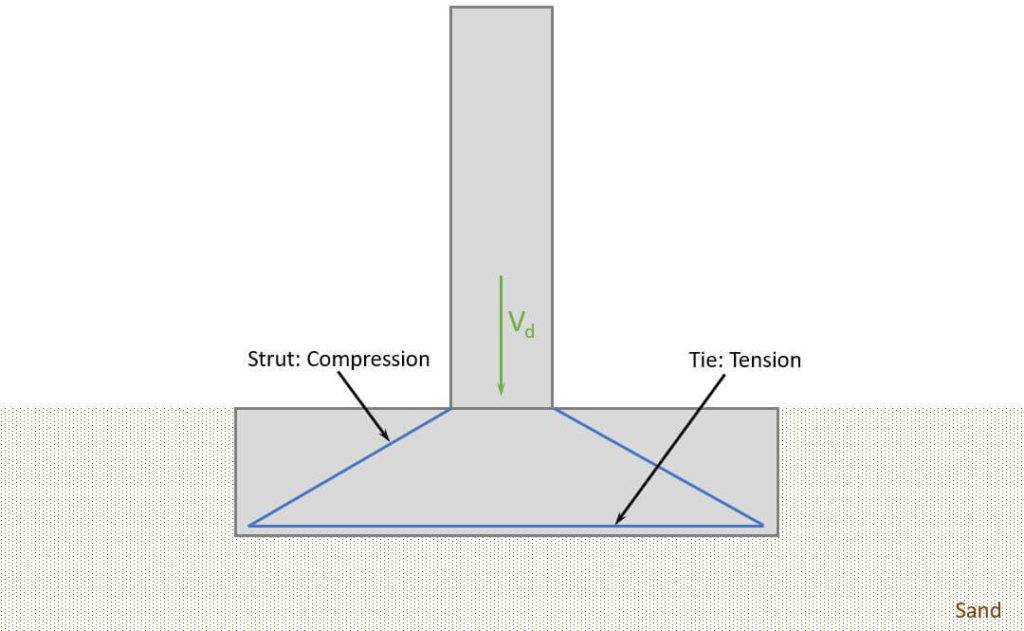
Now, as concrete can’t take much tension, reinforcement will be used for the tie, and we are going to calculate how much.
The compression zone of the pad foundation creates pressure in the soil, which is visualized in the next picture.
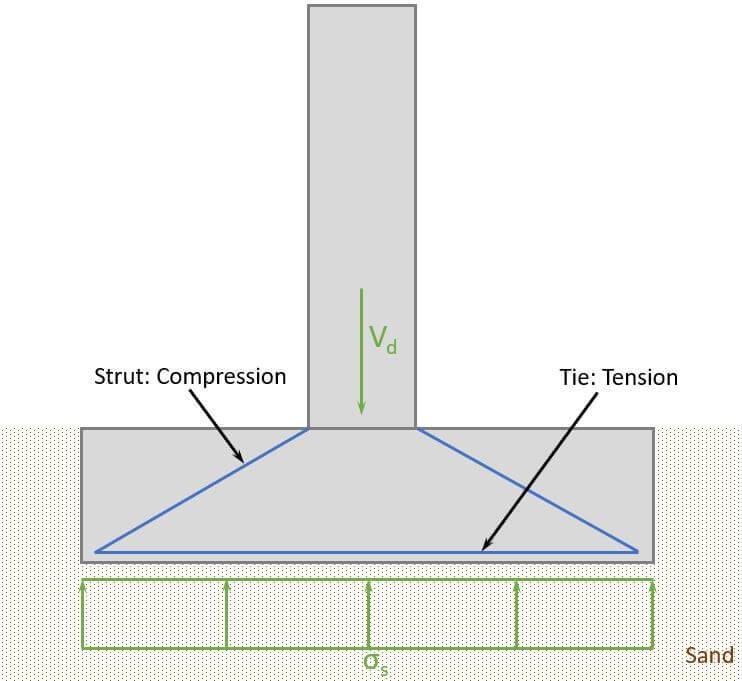
$$\sigma_s = \frac{V_d}{w \cdot l} = 361.1 kN/m^2$$
The soil pressure $\sigma_s$ creates a bending moment in the pad foundation, and we use a cantilever beam to calculate that bending moment.
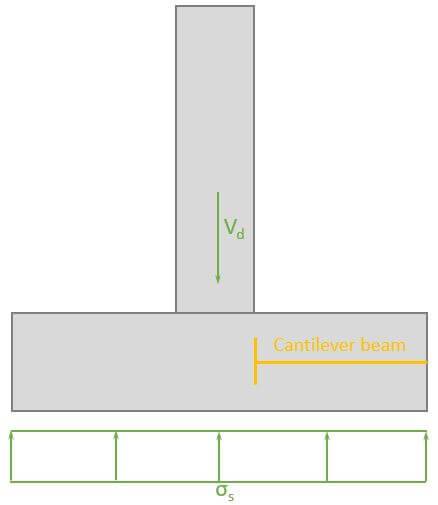
The length of the cantilever is $l_c = w/2 – w_c/2 = 0.85 m$
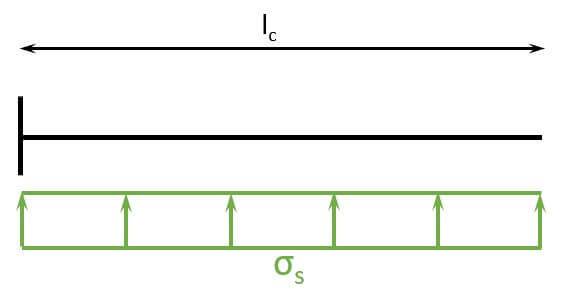
Now, the bending moment can be calculated.
$$M_{Ed} = \sigma_s \cdot l \cdot l_c \cdot l_c/2 = 361.1 kN/m^2 \cdot 2.1 m \cdot 0.85 m \cdot \frac{0.85 m}{2} = 273.9 kNm$$
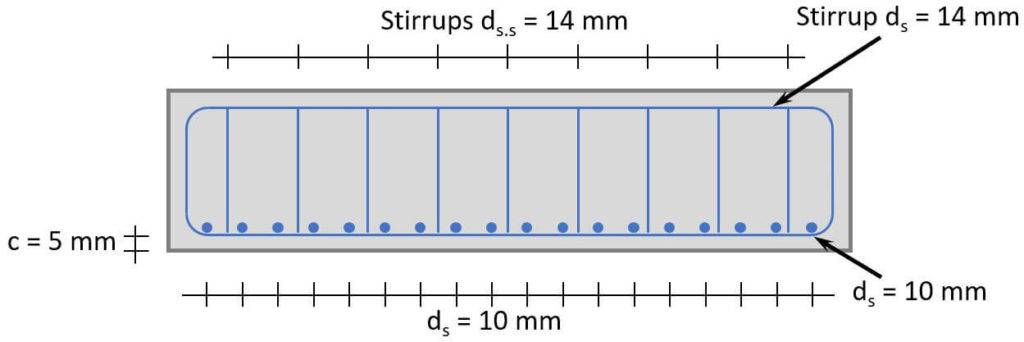
We set the diameter of the rebars to $d_s = 10 mm$.
The lever arm of the upper layer of reinforcement is calculated as
$$d = h – c – d_s – \frac{d_s}{2} = 0.44 m$$
The required reinforcement is calculated with the following formulas. 👇👇
$$\mu = \frac{M_{Ed}}{w \cdot d^2 \cdot \eta \cdot f_{c.d}} = 0.033$$
$$\omega = 1 – \sqrt{1 – 2 \cdot \mu} = 0.034$$
$$A_{s.req} = \omega \cdot \frac{w \cdot d \cdot \eta \cdot f_{c.d}}{f_{y.d}} = 1398 mm^2$$
Cross-sectional area of a rebar with $d_s = 10 mm$.
$$A_{s.1} = \pi \cdot (\frac{d_s}{2})^2 = 78.5 mm^2$$
Amount of rebars:
$$n = roundup(\frac{A_{s.req}}{A_{s.1}}) = 18$$
Reinforcement area:
$$A_s = n \cdot A_{s.1} = 1414 mm^2 > A_{s.req}$$
Check of minimum reinforcement according to EN 1992-1-1 9.2.1.1 (9.1N).
$$A_{s.min} = max(0.26 \cdot \frac{f_{ctm}}{f_{y.k}} \cdot w \cdot d; 0.0013 \cdot w \cdot d) = 1252 mm^2$$
Because $A_{s.min} < A_s$, 18 rebars of diameter $d_s = 10 mm$ are used.
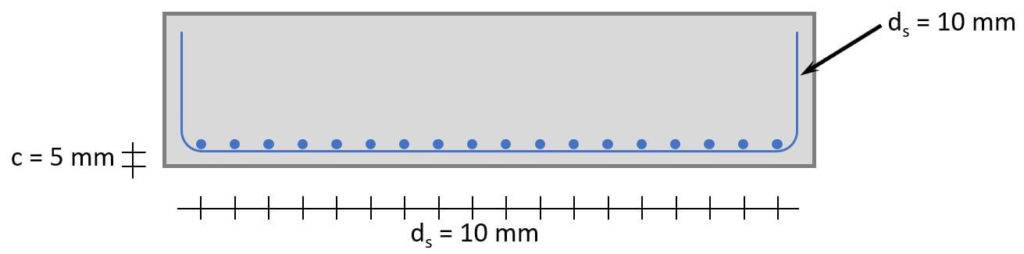
👩🏫 Reinforced Concrete Design – Shear Verification
First we check if shear reinforcement is required according to EN 1992-1-1 6.2.2.
Members not requiring design shear reinforcement
EN 1992-1-1 6.2.2 (1)
$$k = 1 + \sqrt{\frac{200}{\frac{d}{mm}}} = 1.68$$
$$\rho_1 = min(\frac{A_s}{w \cdot d}; 0.02) = 0.002$$
Design value of the shear resistance (EN 1992-1-1 (6.2.a))
$$\upsilon_{Rd.c} = max(\frac{0.18}{\gamma_c} \cdot k \cdot (100 \rho_1 \cdot f_{c.k})^{\frac{1}{3}}; \frac{0.051}{\gamma_c} \cdot k^{\frac{3}{2}} \cdot \sqrt{f_{c.k}}) = 0.419 MPa$$
$$V_{Rd.c} = \upsilon_{Rd.c} \cdot w \cdot d = 382.5 kN$$
Shear reinforcement required because $V_d > V_{Rd.c}$.
Members requiring design shear reinforcement
EN 1992-1-1 Figure 6.5
$$z = 0.9 \cdot d = 0.39m$$
Coefficient taking into account the state of the stress in the compression chord:
$$\alpha_{cw} = 1.0$$
Strength reduction factor for concrete cracked in shear (EN 1992-1-1 (6.9))
$$\upsilon_1 = 0.6$$
$$cot(\theta) = 2.5$$
$$tan(\theta) = 0.4$$
Shear resistance (EN 1992-1-1 (6.9))
$$V_{Rd.max} = \alpha_{cw} \cdot w \cdot z \cdot \upsilon_1 \cdot \frac{f_{c.d}}{cot(\theta) + tan(\theta)} = 3519 kN$$
Verification is fulfilled. 👇👇
$$V_d < V_{Rd.max} = 1$$
Reduction of the design yield strength of the reinforcement (EN 1992-1-1 (6.8))
$$f_{ywd} = 0.8 \cdot f_{y.k} = 440 MPa$$
Shear links (EN 1992-1-1 (6.8))
$$A_{sw} = \frac{V_d}{z \cdot f_{ywd} \cdot cot(\theta)} = 3698 \frac{mm^2}{m}$$
Inclination of the shear reinforcement
$$\alpha = 90 deg$$
Maximum spacing (EN 1992-1-1 (9.6N))
$$s_{l.max} = 0.75 \cdot d \cdot (1 + cot(\alpha)) = 0.326 m $$
We set the spacing of the bars to s = 250 mm.
Shear reinforcement required for the whole width:
$$A_{sw} = A_{sw} \cdot w = 7765 mm^2$$
Amount of bars:
$$n = roundup(\frac{w}{s}) = 9$$
Required cross-sectional area for one stirrup:
$$A_{sw.req} = \frac{A_{sw}}{2 \cdot n} = 431.4 mm^2$$
Required bar diameter:
$$d_{s.req} = \frac{2 \cdot \sqrt{A_{sw.req}}}{\pi} = 13.2 mm$$
Therefore, a stirrup diameter of $d_{s.s} = 14 mm$ is picked.
🙌 Conclusion
Once the bearing capacity of the sand, longitudinal and shear reinforcement of the pad foundation are verified, we successfully designed the pad foundation.💯💯
If you are new to structural design, then check out more of our design tutorials where you can also learn how to design wood elements such as
But now, I would like to hear from you: Have you already designed a pad foundation in university or at your work? And which semester was that in? Tell us a bit about the structure it was supporting, as we all want to learn from each other.✍️
🙋♂️ Pad Foundation FAQ
A pad foundation is a type of foundation that supports a concentrated load from for example a column. It consists of a thick concrete slab that is reinforced with steel bars and is in most cases embedded in soil.
Pad foundations are designed for geotechnical (EN 1997-1) and reinforced concrete (EN 1992-1-1) capacities. In the geotechnical design, the geometry of the pad foundation is found, which the soil can resist. In the concrete design, the longitudinal and shear reinforcement is calculated.
![How To Dimension Rafters Of Purlin Roofs? [Structural Guide]](https://www.structuralbasics.com/wp-content/uploads/2022/03/How-to-design-rafters-of-purlin-roofs-768x439.jpg)