Point Loads: What They Are and How to Calculate Them
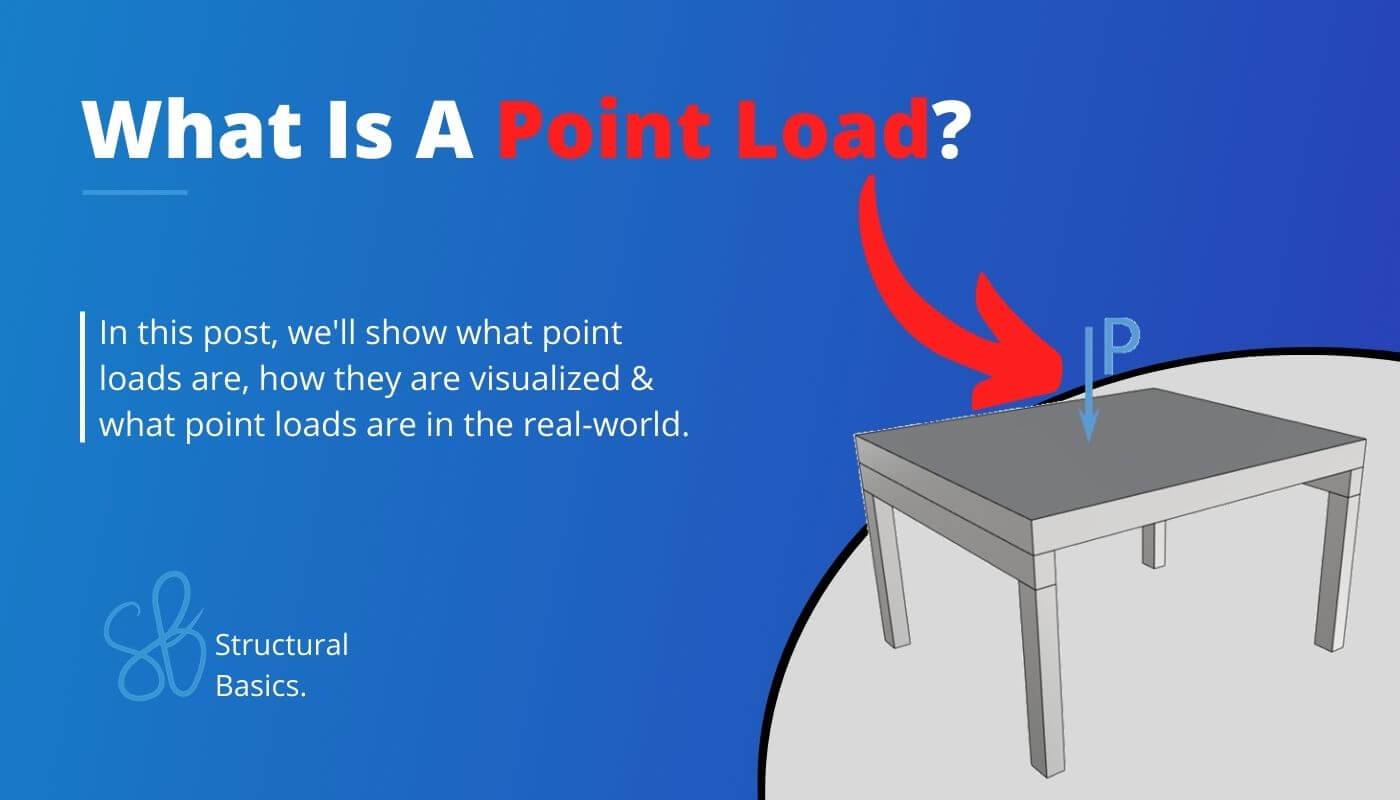
Point loads can be tricky to understand if you aren’t trained in engineering or physics.
Questions arise such as: 🙋♀️🙋♀️
How do engineers account for point loads in their structural designs? And why is it important to understand point loads in the first place? Or how do you calculate the magnitude?
In this blog post, we’ll break it down. 📝📝
We’ll show you, step-by step, what a point load is, how it’s visualized in engineering, real-world examples and much more.
So let’s get started. 🚀🚀
Definition – Point Load
A point load is a concentrated action (load) on a structural element such as a beam or column which acts only on a very small area compared to the uniformly distributed load.
In structural engineering, point loads are a simplification of complex actions.
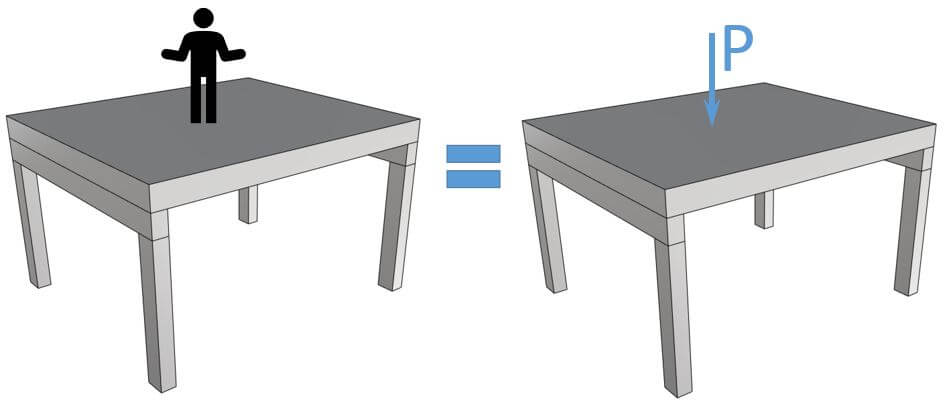
The self-weight of a person standing on a floor and the force that a screw applies on a wooden board are examples of point loads.
Alright, let’s look at how we use point loads in mechanics and how we apply point loads to static systems. ⬇️⬇️
Visualization of Point Loads
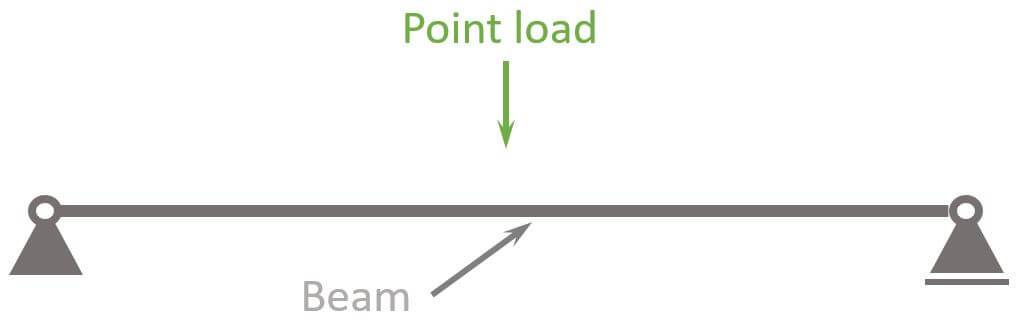
The point load is represented as an arrow. This arrow is then applied to a static system like a simply supported beam, or column.
The picture below shows a point load applied to a simply supported beam.👇👇
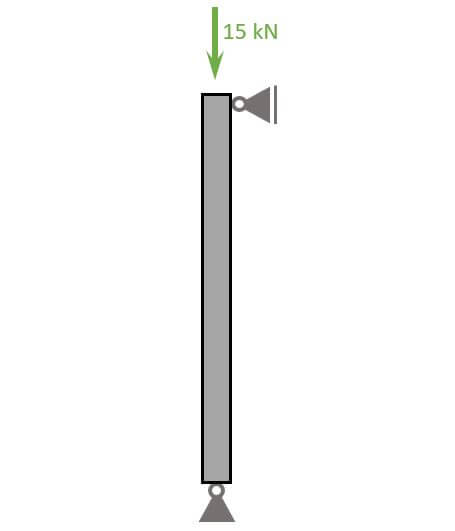
Loads on columns are usually applied vertically to the top of the beam as the next picture shows.
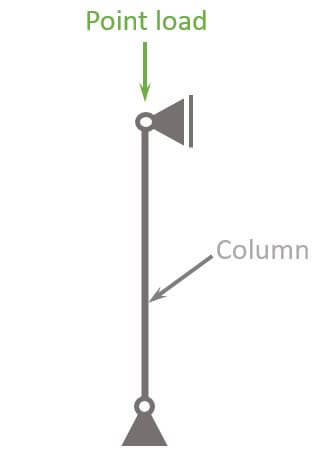
In a later section, we’ll show how to transform an area load to a line load and then to a point load.
So stick with us! 🙌🙌
Values and Units
Point loads have values and units, and based on these, the internal forces of the structural element are calculated.
Once the internal forces are known, the structural element can be designed (cross-sectional dimensions are found).
The unit of the point load is kN (kilonewton). This applies to Europe and anywhere where Eurocode is used.
In the US, kip (kips = kilo-pounds) is used as unit.
Every point load has a value which stands in front of the uni. So let’s have a look at a picture. 👇👇
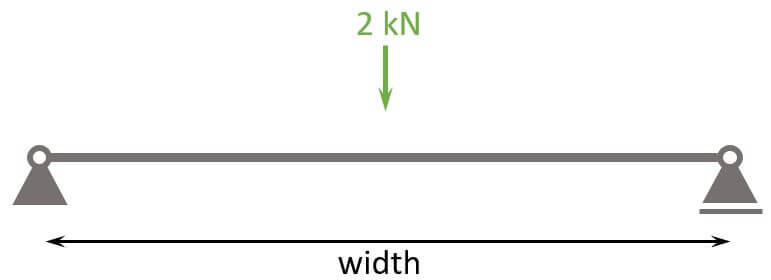
Point Load Examples
Point loads can come from a variety of different load types, such as:
- Snow load
- Wind load
- Dead load
- Live load
- Earth pressure
We have written an extensive article about loads on buildings, where we go into detail with every load type. So check that out if you want to learn more.
It’s mostly not about the load type, but rather the element that takes up the load. Dead and live loads transferred from slabs to beams and then to columns are applied as point loads to the columns.
But the same loads transferred to beams are applied as line loads to the beams.
Don’t worry, we’ll have examples about the load transfer later in this article.
But now, let’s look at some practical examples.
Design loads on a timber column of a highrise building
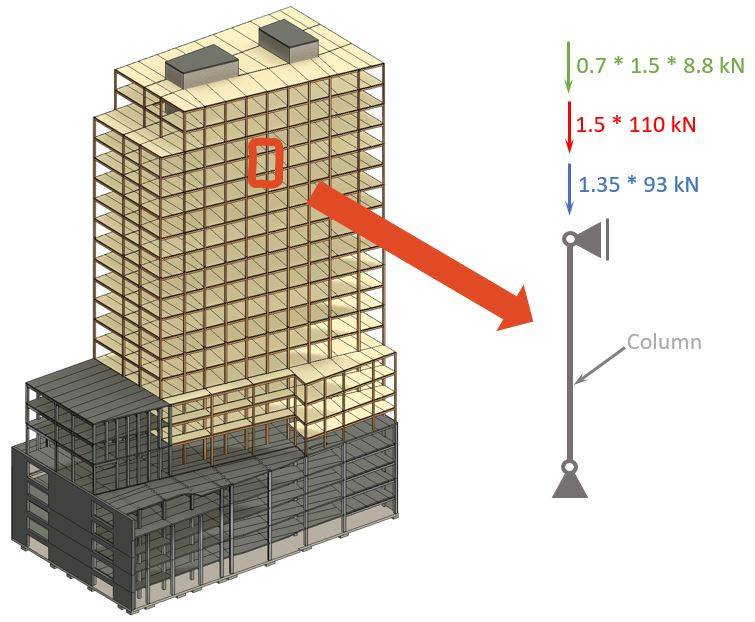
The 3 different loads are dead load🟦, live load🟥 and snow load🟩 which were initially applied to the slabs as area loads and to the beams as line loads.
If you wonder, why we apply all 3 loads at the same time and with factors to the column. That’s because for every structure, we do load combinations to account for “real situations” and extra safety.
You can find a full structural guide on how to design this timber column here.
Loads applied to the nodes of the warren truss
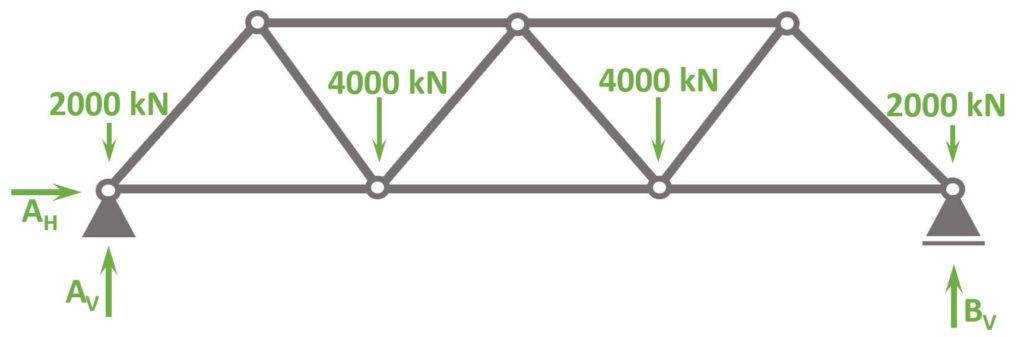
A uniformly distributed design load of 200 kN/m is applied on the bottom chords of the warren truss. But because the elements are all bars, the line load needs to be transformed into point loads to calculate the reaction and normal forces with the 3 equilibrium equations.
These design loads are the result of load combinations of traffic and dead load.
You can check out our calculation guide for warren trusses here.
Now, let’s have a look at how we convert area loads into line loads and then point loads. 🚀🚀
Transformation of Area Load to Point Load
Let’s run through the example where a UDL area load of 2 kN/m2 is applied to a slab.
The slab is supported by 2 beams which have a distance of 5 m.
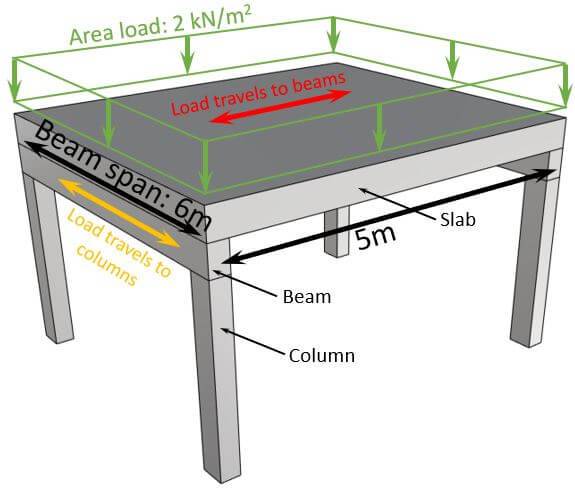
To calculate the UDL line load that you can apply on 1 of the beams, we multiply the area load with half of the distance of the 2 beams.
$$2 \frac{kN}{m^2} \cdot \frac{5m}{2} = 5 \frac{kN}{m}$$
Now, to get the point loads which act on the columns, we calculate the reaction forces of the simply supported beams. 👇👇
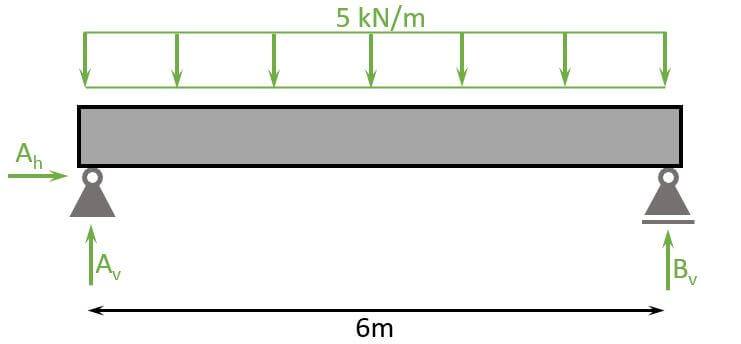
With the horizontal and vertical equilibrium equations, we can now calculate the reaction forces as:
$$\sum H = 0: A_h = 0$$
$$\sum V = 0: A_v + B_v – 5kN/m \cdot 6m = 0$$
$$A_v = B_v = 5kN/m \cdot \frac{6m}{2} = 15 kN$$
As Ah = 0, there is only a vertical load that acts on the columns.
Point Load On A Beam
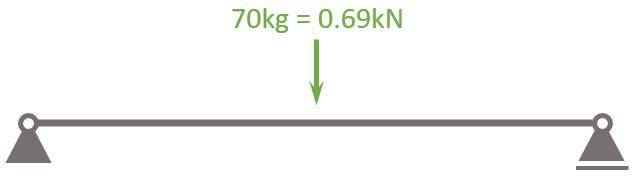
An example of a point load on a beam is a person sitting on a beam like in the next picture.
Now, this same beam with the person can be represented as in the next picture ⬇️⬇️. If the person weighs 70 kg, then the point load is 0.69 kN.
Another example is the support forces of rafters on purlins.
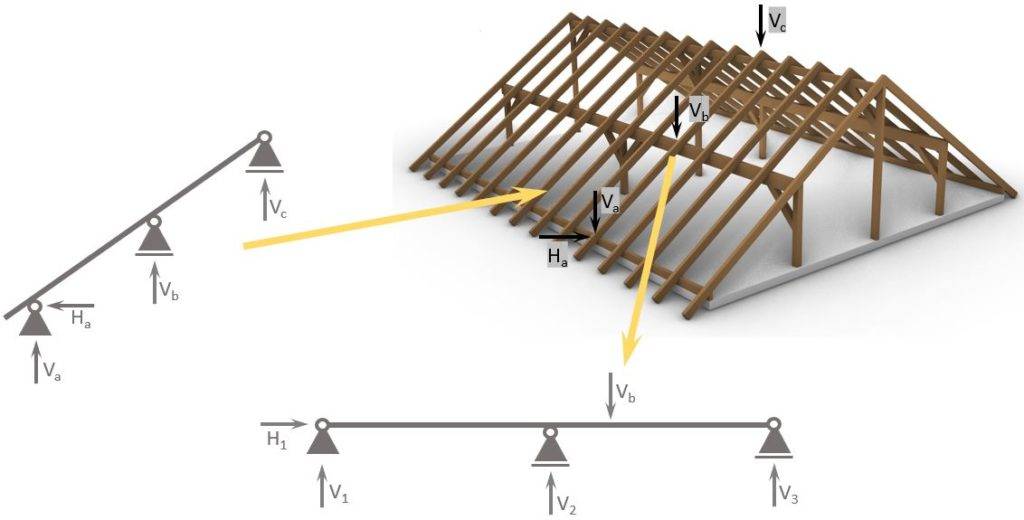
Conclusion
Now, that you got an understanding of point loads, you can learn about the other loads that act on beams.
Once you are confident with the different types of loads, you can calculate the reaction and internal forces.
Then, finally, structural elements can be designed with different materials based on the internal forces. Check out our structural guides. 👇👇
I hope that this article helped you understand point loads. In case you still have questions, let us know in the comments below. ✍️✍️
Point Load FAQ
1. A person sitting on a bench
2. A book placed on a shelf
3. A truck driving on a bridge
Point loads act in one local spot, while uniformly distributed loads act across an area or path. Both load types also have different units. The unit of point loads is kN, while uniformly distributed loads are in kN/m2 or kN/m.
![Uniformly Distributed Load [All YOU Need To Know]](https://www.structuralbasics.com/wp-content/uploads/2023/04/Uniformly-distributed-loads-768x439.jpg)
